В книге Г. Коэна «Обо всё можно договориться» утверждается: «Успешный подход к пе-реговорам заключается в выяснении того, что в действительности нужно противной стороне, и в доведении до её сознания того, каким образом она могла бы добиться желаемого, не мешая мне получить своё». Эта цитата определяет очень разумный подход к взаимодействию участни-ков с несовпадающими интересами, фокусирующийся на сотрудничестве, а не на соперничест-ве. Мы видим, что взаимодействия самого различного рода, в которых в той или иной степени присутствуют и конфликты, и сотрудничество, встречаются постоянно − и в нашей повседнев-ной жизни, и в профессиональной деятельности, и в окружающей нас действительности. Деле-ние наследства или имущества при разводе, согласование различных точек зрения при принятии решений, спортивные соревнования и творческие конкурсы, выделение квот партиям или терри-ториям в выборном органе, распределение различных видов работ между сотрудниками, доступ к компьютерным ресурсам при работе операционных систем и пользовательских программ, борьба за существование между хищниками и жертвами, переговоры о разоружении между су-пердержавами − всё это примеры взаимодействий, естественно сочетающих конфликты и со-трудничество.
Важность и распространённость таких взаимодействий уже с давних пор привлекали вни-мание представителей различных видов профессиональной деятельности − математиков, управ-ленцев, психологов, политологов, социологов, военных и других специалистов.
На многочисленные ситуации такого типа естественно смотреть с двух разных точек зре-ния, которые условно можно назвать внутренней и внешней. С внутренней точки зрения мы ассоциируем себя с одним из участников взаимодействия (или же на самом деле являемся им), пытаясь добиться наилучших для этого участника результатов, при том, что действия других участников (также преследующих свои цели) от нас не зависят. В силу такой точки зрения эта проблематика ориентирована больше на конфликты, чем на сотрудничество. Она относится к теории игр, является хорошо и подробно исследованной и имеет многочисленные приложения в самых разных реальных ситуациях. С внешней точки зрения мы ассоциируем себя не с одним из участников взаимодействия, а с теми людьми и ∕ или ведомствами, которые организуют это взаи-модействие и разрабатывают правила, в рамках которых оно и проистекает. При этом предпола-гается, что результат взаимодействия всех участников, которые преследуют свои индивидуаль-ные цели, будет достаточно разумным с более общей точки зрения, которая больше ориентиро-вана на сотрудничество, чем на конфликт. Люди и организации, заинтересованные в результатах подобных взаимодействия и разрабатывающих их правила, иногда называются метаигроками, что подчёркивает их особую – по сравнению с остальными участниками – роль.
В отличие от теории игр, общей теории взаимодействия с указанной точки зрения нет, од-нако есть важные результаты, полученные в рамках отдельных направлений. Достаточно извест-ным примером такого рода постановок является синтез механизмов в институциональной эко-номике, когда игроками являются экономические агенты, а в роли метаигрока, определяющего правила их взаимодействия, выступает государство (в лице соответствующих властных струк-тур). Однако с такой точки зрения можно рассмотреть и многие другие процессы и явления в са-мых различных сферах. Примером такой постановки является и выработка правил агрегации индивидуальных предпочтений, и разработка систем пропорционального представительства, и правила справедливого дележа, и алгоритмы предоставления вычислительных ресурсов процес-сам в современных ЭВМ, и многие другие ситуации, связанные с разработкой оптимальных или хотя бы разумных правил взаимодействия участников. Некоторые из этих вопросов, наряду с более традиционными постановками теории игр, и составляют материал данной части пособия.
В него входят три главы. Глава 11 «Матричные игры» посвящена самому базовому и простому классу игр – конечным играм двух участников с нулевой суммой. В главе 12 «Другие игровые модели» рассмотрены – на самом простом уровне – другие классы игр: биматричные и позици-онные. Наконец, в главе 13 «Организация взаимодействия» представлены результаты анализа взаимодействия с упомянутой внешней точки зрения в трёх достаточно известных и практичес-ки интересных ситуациях.
Глава 11. Матричные игры
1. Понятие матричной игры
2. Решение игры
3. Удаление стратегий
4. Смешанное расширение матричных игр
5. Решение игр размерности 2´2 и 2´ n в смешанных стратегиях
6. Предметный указатель
Понятие матричной игры
В этой главе будет рассмотрена простейшая модель конфликтных ситуаций - матричные игры двух лиц. Изложим эту модель, учитывая, что некоторые её свойства присущи значительно более сложным конфликтам. Сначала дадим содержательное описание моделируемой ситуации.
В игре участвуют два игрока (скажем, A и B). У каждого игрока имеется конечное число возможных действий, которые обычно называются стратегиями. Природа этих действий мо-жет быть самой разнообразной, но сама по себе она не имеет значения. Каждый игрок выбирает одну из своих стратегий независимо от другого игрока. Реально это значит, что игрок A не зна-ет, какую стратегию выбирает игрок B, а игрок B не знает, какую стратегию выбирает игрок A. После того, как оба выбора сделаны, игрок A получает выигрыш, зависящий от обеих выбран-ных стратегий. Если выигрыш - положительное число, то игрок B платит игроку A соответст-вующую сумму (в заранее обговорённой валюте); в противном случае игрок A платит игроку B. Игрок A стремится максимизировать свой выигрыш, а игрок B стремится минимизировать свой проигрыш.
При формальном описании игры в силу конечности множеств стратегий у обоих игроков без ограничения общности можно считать, что сами стратегии задаются натуральными числами от 1 до m у игрока A и от 1 до n у игрока B. Поэтому выигрыш игрока A можно задавать платёжной матрицей Q размера m ´ n: если игроки выбрали стратегии i Î{1,..., m } и j Î{1,..., n }, то выигрыш игрока A равен числу qij - элементу матрицы Q, стоящему на пересечении i -ой строки и j -го столб-ца. Напомним, что проигрыш игрока B считается равным выигрышу игрока A. Можно считать, что выирыш игрока B при выборе стратегий i Î{1,..., m } и j Î{1,..., n } равен числу - qij. Игры, в которых суммарный выигрыш всех игроков равен нулю, называются играми с нулевой суммой). Таким образом, матричная игра двух лиц является - по определению - игрой с нулевой суммой.
Решение игры
В матричной игре с платёжной матрицей Q игрок A стремится максимизировать свой выигрыш при любом выборе стратегии игроком B. Предположим, что он выбирает стратегию i Î{1,..., m }. Поскольку игрок A не знает, какую именно стратегию (т.е. какой индекс j) выбрал игрок B, то всё, что он может себе гарантировать - это выгрыш в размере
gi = 
. (1)
Естественно, что игрок A выберет такую стратегию i Î{1,..., m }, которая максимизирует его гарантированный выгрыш gi. Поэтому он выбирает стратегию i *, для которой
= 
. (2)
Заметим, что при любом i Î{1,..., m } выражение , входящее в (2), не зависит от j. Поэтому значение зависит только от платёжной матрицы Q. Любая стратегия i *, удовлетво-ряющая условию (2), называется оптимальной стратегией игрока A (оптимальная стратегия i * может определяться неоднозначно, так как gi может быть максимальным при различных i Î{1,..., m }).
Проведённые рассуждения показывают, что именно должен делать игрок А, чтобы до-биться максимально возможного гарантированного выигрыша. Величина , которая определя-ется только по платёжной матрице Q, называется нижней ценой игры и обозначается через V -.
Игрок B стремится минимизировать свой проигрыш. Предположим, что он выбирает стра-
тегию j Î{1,..., n }. Поскольку игрок B не знает, какую именно стратегию выбрал игрок А, то
всё, что он может себе гарантировать - это проигрыш в размере
fj = 
. (3)
Естественно, что игрок B выберет такую стратегию j Î{1,..., n }, которая минимизирует его га-рантированный проигрыш fj. Поэтому он выбирает стратегию j *, для которой
= 
. (4)
Как и значение , значение зависит только от платёжной матрицы Q. Любая стратегия j *, удо-влетворяющая условию (4), называется оптимальной стратегией игрока B (оптимальная страте-гия j *может определяться неоднозначно, так как fj может быть минимальным при различных j Î{1,..., n }).
Проведённые рассуждения показывают, что именно должен делать игрок B, чтобы до-биться минимально возможного гарантированного проигрыша. Величина , которая определя-ется только по платёжной матрице Q, называется верхней ценой игры и обозначается через V +.
В силу теоремы о минимаксе для любой матрицы Q имеет место неравенство
≤ (5)
или, с учётом (2) и (4),
V - ≤ V +.
Таким образом, гарантированный выигрыш игрока А не может быть больше гарантированного проигрыша игрока B.
В теории игр особенно важны те случаи, когда нижняя и верхняя цены игры совпадают. Общее значение V = V -= V +. называется ценой игры. При этом имеет место следующее
Утверждение 1. 1) V -= V + тогда и только тогда, когда некоторый элемент 
платёжной матрицы Q является одновременно максимальным в её i* -ой строке и минимальным в её j* -ом столбце, т.е. для любых i Î{1,..., m } и j Î{1,..., n }
≤ ≤ 
. (6)
2) цена игры V совпадает с ; 3) стратегии i* и j* являются оптимальными ■
Пара стратегий á i*, j* ñ, удовлетворяющих требованиям утверждения 1, может определять-ся неоднозначно. Однако для всех таких пар á i*, j* ñ элементы платёжной матрицы Q равны одному и тому же числу - цене игры V. Всякий элемент платёжной матрицы Q, который является одновременно максимальным в i* -ой строке и минимальным в j* -ом столбце, называ-ется седловой точкой матрицы Q.
Заметим, что в силу неравенств (6) любому игроку оказывается невыгодным менять опти-мальную стратегию, если другой игрок будет придерживаться своей оптимальной стратегии. Для игрока А это следует из 1-го неравенства, для игрока В - из 2-го неравенства. Именно в силу разумности одновременного выбора игроками в данной ситуации своих оптимальных стратегий, любая пара стратегий á i*, j* ñ, удовлетворяющих требованиям утверждения 1, называ-ется решением игры.
Решения существуют далеко не у всех игр рассматриваемого типа. Как выбирать страте-гии в случае отсутствия седловых точек у платёжной матрицы, будет показано в разделе 4 дан-ной главы.
Пример 1. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей:
Q = 
. (7)
Найдём, в соответствии с формулами (1) и (2), оптимальные стратегии игрока А. По фор-муле (1)
g 1= 
= min{7, 6, 5, 4} = 4;
g 2=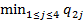 
= min{1, 8, 2, 3} = 1;
g 3= 
= min{8, 1, 3, 2} = 1.
По формуле (2) = max{4, 1, 1}, откуда следует, что оптимальная стратегия i * = 1 и нижняя цена игры V -= 4.
Найдём, в соответствии с формулами (3) и (4), оптимальные стратегии игрока В. По фор-муле (3)
f 1= 
= max{7, 1, 8} = 8;
f 2= 
= max{6, 8, 1} = 8;
f 3= 
= max{5, 2, 3} = 5;
f 4= 
= max{4, 3, 2} = 4.
По формуле (4) = min{8, 8, 5, 4} = 4, откуда следует, что оптимальная стратегия j * = 4 и верхняя цена игры V += 4.
Таким образом, нижняя цена игры совпадает с верхней ценой. Как и должно быть по ут-верждению 1, цена игры 4 равна = q 14. Пара стратегий á1, 4ñ является решением игры и седловой точкой матрицы Q ■
Пример 2. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей:
Q = 
, (8)
все элементы которой, кроме q 24, совпадают с соответствующими элементами платёжной матрицы из примера 1.
Найдём, в соответствии с формулами (1) и (2), оптимальные стратегии игрока А. По фор-муле (1)
g 1= = min{7, 6, 5, 4} = 4;
g 2= 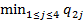= min{1, 8, 2, 5} = 1;
g 3= = min{8, 1, 3, 2} = 1.
По формуле (2) = max{4, 1, 1}, откуда следует, что оптимальная стратегия i * = 1 и нижняя цена игры V -= 4.
Найдём, в соответствии с формулами (3) и (4), оптимальные стратегии игрока В. По фор-муле (3)
f 1= = max{7, 1, 8} = 8;
f 2= = max{6, 8, 1} = 8;
f 3= = max{5, 2, 3} = 5;
f 4= = max{4, 5, 2} = 5.
По формуле (4) = min{8, 8, 5, 5} = 5, откуда следует, что множеством оптимальных страте-гий j * является множество {3, 4} и верхняя цена игры V + = 5.
Таким образом, в данном случае, в отличие от примера 1, нижняя цена игры не равна верхней цене. Поэтому для данной платёжной матрицы Q решений игры, как и седловых точек, нет ■
Для любой матричной игры верно следующее
Утверждение 2. При прибавлении любого числа a (положительного или отрицательного) ко всем элементам платёжной матрицы Q множества оптимальных стратегий обоих игроков не изменяются, а нижняя и верхняя цена игры получены из исходных прибавлением того же числа a ■
В силу утверждения 2 существование решения игры также не зависит от прибавлении ко всем элементам платёжной матрицы Q произвольной константы.
Задание 1. В играх с указанными платёжными матрицами найти оптимальные стратегии обоих игроков, нижнюю и верхнюю цены игры. Указать решение игры, если оно есть; в противном случае явно указать на его отсутствие. В качестве образца см. примеры 1 и 2
| |||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
■
Удаление стратегий
Количество строк и ¤ или столбцов платёжной матрицей может быть уменьшено за счёт удаления доминируемых и дублирующих стратегий. Стратегия s игрока A называется домини-руемой его стратегией t, если все элементы s -ой строки платёжной матрицы не больше, чем со-ответствующие элементы её t -ой строки. Игроку A нет смысла выбирать доминируемую страте-гию s, поскольку при выборе доминирующей стратегии t он выигрывает не меньше, независимо от стратегии игрока B. Стратегия s игрока B называется доминируемой его стратегией t, если все элементы s -го столбца платёжной матрицы не меньше, чем соответствующие элементы её t -го столбца. Игроку B нет смысла выбирать доминируемую стратегию s, поскольку при выборе доминирующей стратегии t он проигрывает не больше, независимо от стратегии игрока A. Стратегия s (любого игрока) называется дублирующей его стратегию t, если соответствующие этим стратегиям строки (или столбцы) совпадают. Очевидно, что из нескольких совпадающих стратегий достаточно оставить только одну, удалив все другие.
Пример 3. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей
| ||||||
В данном случае для игрока A стратегия 1 является доминируемой стратегией 2, для игрока B стратегия 6 является доминируемой стратегиями 3, 4 и 5, а стратегии 4 и 5 являются дублирую-щими друг друга. После удаления указанных доминируемых стратегий и одной из дублирую-щих стратегий останется следующая матрица, в которой доминируемых и дублирующих страте-гий уже нет:
■
Утверждение 3. Удаление доминируемых и дублирующих стратегий из платёжной мат-рицы не влияет на значение нижней и верхней цены игры, заданной данной матрицей. Множес-тва оптимальных стратегий также не меняются (за исключением удаления дублирующих) ■
Таким образом, при удалении из платёжной матрицы «лишних» строк и столбцов суть иг-ры не меняется, в то время как размерность матрицы может значительно уменьшиться. В при-мере 3 вместо матрицы размера 4´6 получена матрица размера 3´4.
Пример 4. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей:
В данной матрице 1-ая строка доминируема 2-ой строкой, поскольку все её элементы больше. После удаления 1-ой строки получаем следующую матрицу:
В новой матрице 1-ый и 4-ый столбцы доминируемы 3-им столбцом. После их удаления оста-нется матрица
в которой 1-ая строка доминирует 2-ую строку. После удаления 2-ой строки останется единст-венная строка á28, 18, 33ñ, откуда следует, что игроку B надо выбрать 2-ой столбец, содержа-щий минимальный проигрыш 18, т.е. исходная матрица сведена к матрице размера 1´1, или од-ному числу 18. Возвращаясь к исходной матрице, видим, что пара стратегий á2, 3ñ является решением данной игры, а её цена равна 18.
Начнём теперь в исходной платёжной матрице с удаления доминируемых столбцов, а не строк, как делали выше. После удаления доминируемого 1-го стобца получаем
Далее, удаляя доминируемые 1-ую и 3-ью строку, получаем единственную строку á28, 18, 38, 33ñ, и выбирая в ней минимальный проигрыш 18, получаем тот же ответ - матрицу размером 1´1, т.е. число 18 ■
Результат примера 4 не случаен. Имеет место
Утверждение 4. При любом порядке удаления доминируемых и дублирующих стратегий получаем одну и ту же матрицу, в которой удаляемых строк и столбцов больше нет ■
Задание 2. Удалить доминируемые стратегии в следующих матрицах (см. примеры 3 и 4)
| |||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
■
