Глава 12. Другие игровые модели

 

1. Биматричные игры

2. Позиционные игры

3. Предметный указатель

 

В этой главе будут рассмотрены несколько различных конфликтных ситуаций, для анали-за которых используется общий термин - игра. При всех различиях общим для моделируемых ситуаций является

1) наличие лвух или более участников (игроков) с несовпадающими, хотя и не обязатель-но противоположными, интересами;

2) формальное описание взаимодействия игроков, т.е. правил игры;

3) зависимость выигрыша каждого игрока от стратегий (действий, «ходов») остальных иг-роков.

Из большого числа разнообразных классов игр рассмотрены - на самом простом уровне - два из них: биматричные и позиционные игры. Описания указанных классов игр и их решений (в том или ином смысле) приводятся в соответствующих разделах данной главы.

 

1. Биматричные игры y ₀

Из многих видов игр биматричные игры в наибльшей степени похожи на рассмотренные в главе 11 матричные игры (см. раздел 11-1). Как и там, в игре участвуют два игрока A и B, у каждого из которых имеется конечное число стратегий. Игрок выбирает одну из своих страте-гий независимо от другого игрока. После того, как оба выбора сделаны, каждый игрок получает выигрыш или платит проигрыш, которые зависят от обеих выбранных стратегий. В отличие от матричной игры, здесь не предполагается, что выигрыш одного игрока равен проигрышу друго-го. Таким образом, не предполагется, что биматричная игра является игрой с нулевой суммой. Вопрос, кто платит выигрыш и кто получает проигрыш, несмотря на свою важность, в рамках данной модели не рассматривается (организатор игры? рынок? начальство?....). Важно, что со-блюдаются правила, т.е. игроки получают выигрыши и платят проигрыши.

В силу конечности множеств стратегий у обоих игроков без ограничения общности можно считать, что сами стратегии задаются натуральными числами от 1 до m у игрока A и от 1 до n у игрока B. Поэтому выигрыш игрока A можно задавать платёжной матрицей А размера m ´ n, а выигрыш игрока В - платёжной матрицей В того же размера. Если игроки выбрали страте-гии i Î{1,..., m } и j Î{1,..., n }, то выигрыш игрока A равен числу a_ij - элементу матрицы А, стоя-щему на пересечении её i -ой строки и j -го столбца, a выигрыш игрока В равен числу b_ij - эле-менту матрицы B, стоящему на пересечении её i -ой строки и j -го столбца.

Пример 1. Игра Аумана. Дадим описание этой игры. Каждый участник может обратиться к организатору игры с одной из двух возможных просьб, которая будет обязательно выполнена. Просьбы таковы:

1. Дать сто долларов другому игроку;

2. Дать один доллар мне.

Выбор просьбы и есть выбор стратегии. Запишем обе платёжные матрицы:

А = , B = .

Проанализируем все 4 возможности. Если оба игрока выбирают 1-ые стратегии, то у каждого будет $ 100, что и выражено числом 100 в верхнем левом углу обеих матриц. Если игрок A выбрал 1-ую стратегию, а игрок В - 2-ую стратегию, то игрок A не получает ничего, а игрок В -$ 101 (число a ₁₂ = 0, а число b ₁₂ = 101). Если же игрок A выбрал 2-ую стратегию, а игрок В - 1-ую стратегию, то число a ₂₁ = 101, а число b ₂₁ = 0. Наконец, если оба игрока выбирают 2-ые стратегии, то у каждого будет $ 1, что и выражено числом 1 в правом нижнемм углу обеих матриц.

В данной игре, как и во многих других биматричных играх, более наглядным является представление двух платёжных матриц в виде одной матрицы с парой чисел в каждой позиции i, j, где 1-ое (2-ое) число равно выигрышу игрока A (В) при выборе ими стратегий i и j. В данном случае такая матрица принимает вид:

■ (1)

1.1. Равновесие Нэша. Рассмотренные в главе 11 матричные игры можно рассматривать как частный случай биматричных игр, в которых B = - А. Введём для биматричных игр понятие равновесия Нэша. Оно не только является обобщением понятия решения игры для матричных игр, но и является одним из центральных понятий теории игр в самом широком смысле. Содер-жательно равновесием Нэша является такой набор стратегий разных игроков, при котором ни-кому не выгодно менять свою стратегию, если все остальные игроки свои стратегии не меняют. Напомним, что то же самое верно для решений матричных игр (см. текст между утвержденим 1 и примером 1 в разделе 1.2).

Дадим формальное определение равновесия Нэша (в чистых стратегиях) для рассматрива-емого класса биматричных игр. Пара стратегий á i *, j *ñ называется равновесием Нэша, если

()( j) (( ≤ ) ( ≤ 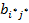)). (2)

Другими словами, если игрок A воспользуется вместо стратегии i * любой другой стратегией i, а

игрок В воспользуется стратегией j *, то в силу неравенства ≤ игрок A не может выиг-рать больше, чем при использовании «равновесной» стратегии i *. То же самое верно и для иг-рока В (в силу неравенства ≤ 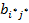). Именно потому, что никто не будет отступать от своей стратегии, такие пары называются равновесиями, а входящие в них стратегии - равновесными.

Пример 2. Рассмотрим важный частный случай, когда у каждого игрока есть две страте-гии. Таким образом, всего имеется 4 пары чистых стратегий: á1, 1ñ, á1, 2ñ, á2, 1ñ, á2, 2ñ. Посколь-ку каждый игрок может поменять свою стратегию 1 или 2 только на одну стратегию (2 или 1), то условия равновесия (2) записываются только для одного i ≠ i * и одного j ≠ j * для каждой из этих пар:

для á1, 1ñ: ( ≤ ) ( ≤ ); (2.11)

для á1, 2ñ: (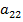 ≤ 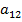) ( ≤ ); (2.12)

для á2, 1ñ: ( ≤ ) ( ≤ 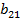); (2.21)

для á2, 2ñ: (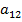 ≤ 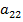) ( 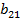≤ ). (2.22)

Суть этих условий в том, что при изменении только одной стратегии у игрока, поменявшего её, выигрыш не может увеличиться - он может остаться тем же или уменьшиться.

Рассмотрим игру Аумана из примера 1, платёжная матрица которой имеет вид (1).

Для того, чтобы пара стратегий á1, 1ñ была равновесием Нэша, по определению требуется выполнение условий (2.11). В силу (1) a ₂₁ = 101, a ₁₁ = 100, т.е. уже 1-ое условие из (2.11) не выполняется. Поэтому пара стратегий á1, 1ñ не является равновесием Нэша.

Для того, чтобы пара стратегий á1, 2ñ была равновесием Нэша, по определению требуется выполнение условий (2.12). В силу (1) a ₂₂ = 1, a ₁₂ = 0, т.е. уже 1-ое условие из (2.12) не выполняется. Поэтому пара стратегий á1, 2ñ не является равновесием Нэша.

Для того, чтобы пара стратегий á2, 1ñ была равновесием Нэша, по определению требуется выполнение условий (2.21). В силу (1) a ₁₁ = 100, a ₂₁ = 101, т.е. 1-ое условие из (2.21) выполняет-ся. Также в силу (1) b ₂₁ = 0, b ₂₂ = 1, т.е. 2-ое условие из (2.21) не выполняется. Поэтому пара стратегий á2, 1ñ не является равновесием Нэша.

Для того, чтобы пара стратегий á2, 2ñ была равновесием Нэша, по определению требуется выполнение условий (2.22). В силу (1) a ₂₂ = 1, a ₁₂ = 0, т.е. 1-ое условие из (2.22) выполняется. Также в силу (1) b ₂₂ = 1, b ₂₁ = 0, т.е. 2-ое условие из (2.22) также выполняется. Поэтому пара стратегий á2, 2ñ является равновесием Нэша.

Заметим, что при выборе обоими игроками 1-ых стратегий оба получают выигрыш 100 - в 100 раз больше, чем они плучают в единственном равновесии Нэша á2, 2ñ. Но при выборе 2-ой стратегии каждый игрок гарантирует себе хотя бы выигрыш 1 независимо от выбора другого игрока, а при выборе 1-ой стратегии такой гарантии нет. Именно в гарантии некоторых, пусть и небольших, выигрышей обоих игроков, суть равновесия Нэша. «Кто не рискует, тот не ужинает с коньячком, а кто рискует, тот вообще не ужинает.» ■

Как и в матричных играх, можно определить оптимальные стратегии для обоих игроков.

Оптимальной чистой стратегией игрока A называется любая стратегия i *, которая макси-мизирует зависящее только от i выражение

. (3a)

Оптимальной чистой стратегией игрока B называется любая стратегия j *, которая макси-мизирует зависящее только от j выражение

. (3b)

Утверждение 1. Пусть пара стратегий á i *, j *ñ является равновесием Нэша. Тогда страте-гии i * и j * оптимальны ■

Нетрудно видеть, что, как в матричных играх может не быть решений в чистых стратеги-ях, так в бимаричных играх может не быть равновесий Нэша в чистых стратегиях.

Пример 3. Рассмотрим биматричную игру со следующей платёжной матрицей: Q = 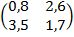. Проверяя, как в примере 2, каждую из 4-ёх пар чистых стратегий á1, 1ñ, á1, 2ñ, á2, 1ñ, á2, 2ñ на выполнение условий (2.11) - (2.22), убеждаемся, что ни одна из них не является равно-весием Нэша ■

Задание 1. В биматричных играх с указанными платёжными матрицами найти все равно-весия Нэша в чистых стратегиях или установить их отсутствие. В качестве образца см. примеры 2 и 3.

■

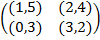
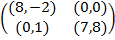
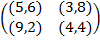
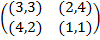
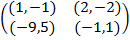
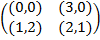
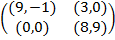
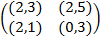
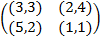
1.2. Смешанное расширение биматричных игр. Понятие смешанного расширения опре-деляется так же, как и для матричных игр. Если игрок A выбирает стратегию i c вероятностью x_i (i = 1,..., m), а игрок B - стратегию j c вероятностью y_j (j = 1,..., n), то говорят, что игроки A и B используют смешанные стратегии x = (x ₁,..., x_m) и y = (y ₁,..., y_n). Чистая стратегия является частным случаем смешанной стратегии, когда все вероятности, кроме вероятности выбора данной чистой стратегии, равны 0, а вероятность выбора данной чистой стратегии равна 1.

Пусть игроки A и B выбрали стратегии x и y. Тогда средние выигрыши игроков A и В определяются формулами

g _A(x, y) = , (4a)

g _B(x, y) = .(4b)

Определим равновесие Нэша в смешанных стратегиях и оптимальные смешанные страте-гии, по аналогии с соответствующими понятиями в чистых стратегий для рассматриваемого класса биматричных игр. Пара стратегий á x *, y *ñ называется равновесием Нэшав смешанных стратегиях, если

()( y) ((g _A(x, y *) ≤ g _A(x *, y *) (g _B(x *, y) ≤ g _B(x *, y *)). (5)

Оптимальной смешанной стратегией игрока A называется любая стратегия x *, которая мак-симизирует зависящее только от x выражение

. (6a)

Оптимальной смешанной стратегией игрока B называется любая стратегия y *, которая мак-симизирует зависящее только от y выражение

. (6b)

Утверждение 2. Пусть пара стратегий á x *, y *ñ является равновесием Нэша. Тогда страте-гии x * и y * оптимальны ■

Принципиальное отличие случая смешанных стратегий от случая чистых стратегий для биматричных игр является аналогом того же отличия для матричных игр (см. утверждение 1.6):

Утверждение 3. Для любой биматричной игры существует равновесие Нэша в смешан-ных стратегиях ■

Напомним, что равновесие Нэша в чистых стратегиях существует не всегда, что и проде-монстрировано в примере 3.

1.3. Нахождение равновесий Нэша в биматричных играх размерности 2×2. Как и на-хождение решений для матричных игр, нахождение равновесий Нэша в смешанных стратегиях для произвольных биматричных игр является вычислительно достаточно сложной задачей - во всяком случае, выходящей за скромные рамки настоящего пособия. Поэтому мы ограничимся слу-чаем, когда у каждого из двух игроков имеется всего две стратегии (игры размерности 2×2). Именно такой игрой является игра Аумана, проанализированная в примерах 1 и 2. В отличие от матричных игр размерности 2×2, описанный ниже способ позволяет находить все равновесия Нэша – как в чистых, так и в смешанных стратегиях.

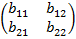Рассматриваемые игры задаются парой матриц A = и B = . У каждо-го игрока есть две чистых стратегии, которым соответствует выбор 1-ым игроком одной из двух строк матрицы A, а 2-ым игроком – одного из двух столбцовматрицы B. При выборе игроками пары стратегий i и j игрок A получает выигрыш a_ij, а игрок B–выигрыш b_ij (i, j = 1, 2). Предста-вим их средние выигрыши (4) в следующем виде:

g _A(x, y) = (a ₁₁ – a ₁₂– a ₂₁ + a ₂₂) xy + (a ₁₂– a ₂₂) x + (a ₂₁– a ₂₂) y + a ₂₂; (7a)

g _B(x, y) = (b ₁₁ – b ₁₂ – b ₂₁ + b ₂₂) xy + (b ₁₂– b ₂₂) x + (b ₂₁– b ₂₂) y + b ₂₂, (7b)

где x и y – вероятности выбора 1-ых чистых стратегий игроками A и B (см. для сравнения формулы (1.20) – (1.23)).

Дальнейшие рассуждения во многом аналогичны рассуждениям из раздела 1.5. Положим

a ₁ = (a ₁₁ – a ₁₂ – a ₂₁ + a ₂₂), (8a)

a ₂ = a ₂₂ – a ₁₂; (9а)

b ₁ = (b ₁₁ – b ₁₂ – b ₂₁ + b ₂₂), (8b)

b ₂ = b ₂₂ – b ₂₁. (9b)

Представим теперь средние выигрыши (7) в виде:

g _A(x, y) = a ₁ xy – a ₂ x + (a ₂₁ – a ₂₂) y + a ₂₂, (10a)

g _B(x, y) = b ₁ xy – b ₂ y + (b ₁₂ – b ₂₂) x + b ₂₂. (10b)

Положив

u = a ₁ y – a ₂, v = (a ₂₁ – a ₂₂) y + a ₂₂, (11a)

s = b ₁ x – b ₂, t = (b ₁₂ – b ₂₂) x + b ₂₂. (11b)

запишем (10) в виде

g _A(x, y) = ux + v, (12a)

g _B(x, y) = sy+t, (12b)

где u и v не зависят от x, s и t не зависят от y. Поэтому при любом фиксированном yg _A(x, y) яв-ляется линейной функцией от x, при любом фиксированном xg _В(x, y) является линейной функ-цией от y. При этом коэффициент u, в силу (11a), является линейной функцией от y, а коэффи-циент s, в силу (11b), является линейной функцией от x. Положим также

y ₀ = a ₂ ¤ a ₁, (13a)

x ₀ = b ₂ ¤ b ₁. (13b)

Из формул (11a), (13a) и (11b), (13b) следует, что при a ₁≠ 0 значение u = a ₁ y ₀ – a ₂ = 0, и при b ₁≠ 0 значение s = b ₁ x ₀ – b ₂ = 0. Графики линейных функций u = a ₁ y – a ₂ в зависимости от a ₁ и a ₂, ко-торые понадобятся для явного построения равновесия Нэша, показаны на рис.1. Графики ли-нейных функций s = b ₁ x – b ₂ не приводятся, так как являются точно такими же.

Перейдём к явному построению равновесий Нэша. Начнём с игрока А. Для любой страте-гии y (напомним, что y – это вероятность выбора 1-ой чистой стратегии игроком В, так что 0 ≤ y ≤ 1) положим

j _A(y) = { x | () (g _A(x', y) ≤ g _A(x, y))}. (14a)

Другими сдовами, j _A(y) – это множество всех стратегий x игрока А, которые максимизирует его выигрыш g _A(x, y) при данном y.

Рис.1a. a ₁= 0, a ₂ = 0

Рис.1b. a ₁= 0, a ₂< 0

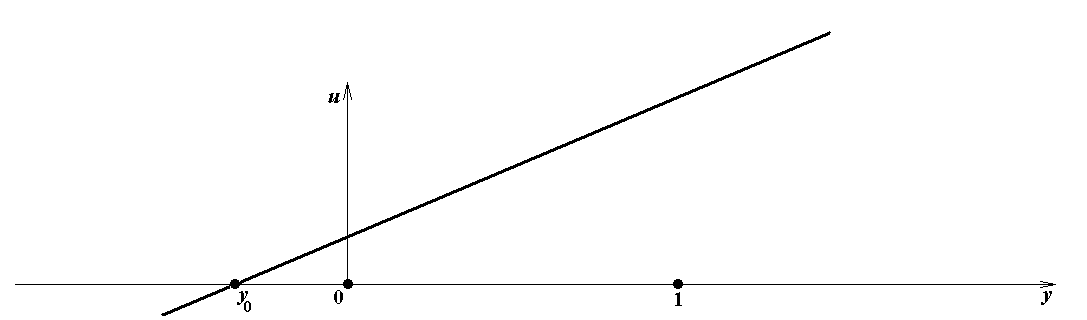
Рис.1c. a ₁> 0, a ₂< 0

 

Рис.1d. a ₂< a ₁< 0

 

Рис.1e. a ₁= 0, a ₂> 0

 

Рис.1f. a ₂> a ₁> 0

 

Рис.1g. a ₁< 0, a ₂> 0

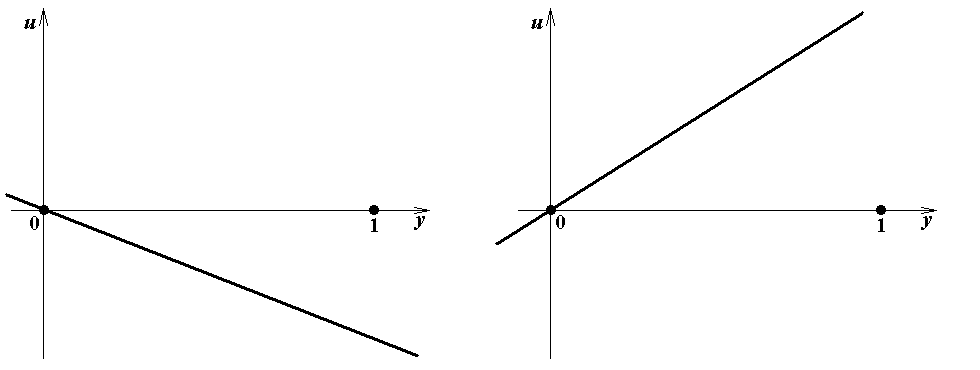
Рис.1h. a ₁< 0, a ₂ = 0 Рис.1i. a ₁> 0, a ₂ = 0

 

Рис.1j. a ₁< 0, a ₂ = a ₁Рис.1k. a ₁> 0, a ₂ = a ₁

 

Рис.1 l. a ₁ < a ₂< 0 Рис.1m. a ₁ > a ₂> 0

 

Имеет место

Утверждение 4. Множество j _A(y) определяется формулой

j _A(y) = (15)

Доказательство. При любом фиксированном y линейная по x функция g _A(x, y) = ux + v (см. (12а)), достигает максимума на отрезке [0, 1] при x = 0, если u < 0, и при x = 1, если u > 0. При u = 0 g _A(x, y) ≡ v, т.е. она не зависит от x. Поэтому её максимум достигается в любой точке отрез-ка [0, 1], что завершает доказательство ■

Положим

Φ _A = {(x, y) | y Î[0, 1], x Î j _A(y)}. (16а)

Множество Φ _A назовём графиком игрока А. Поскольку графики функции u = a ₁ y – a ₂ при любых a ₁ и a ₂ представлены на рис.1, то в силу формул (15) и (16) по ним легко строятся и гра-фики игрока А также при любых a ₁ и a ₂. Остановимся на этом подробнее. При a ₁ = a ₂ = 0 имеем u ≡ 0 (см. рис. 1а), и, следовательно, j _A(y) = [0, 1] при всех y, что показано на рис.2а (график со-стоит из всехточек единичного квадрата). В следующих 3-ёх случаях (рис.1b, 1c и 1d) при 0 ≤ y ≤ 1 имеем u (y) > 0, откуда, в силу (15), j _A(y) ≡ {1}, что показано на рис.2b. В следующих 3-ёх случаях (рис.1e, 1f и 1g) при 0 ≤ y ≤ 1 имеем u (y) < 0, откуда, в силу (15), j _A(y) ≡ {0}, что показа-но на рис.2c.

Далее, для функции u = a ₁ y – a ₂ в случае, показанном на рис.1h, u (0) = 0, u (y) < 0 при y > 0. В силу (15) j _A(0) = [0, 1], j _A(y) = 0 при y > 0, что показано на рис.2d. Аналогично, в случае, по-казанном на рис.1i, j _A(0) = [0, 1], j _A(y) = 1 при y > 0, что показано на рис.2e. В случае, показан-ном на рис.1j, u (1) = 0, u (y) > 0 при y < 1, откуда j _A(1) = [0, 1], j _A(y) = 1 при y < 1, что показано на рис.2f. Аналогично, в случае, показанном на рис.1k, получаем график на рис.2g.

Рис.2a. a ₁= 0, a ₂ = 0 Рис.2b. a ₁= 0, a ₂< 0; a ₁> 0, Рис.2c. a ₁= 0, a ₂> 0; a ₂ > a ₁> 0;

a ₂< 0; a ₂< a ₁< 0 a ₁< 0, a ₂> 0

Рис.2d. a ₁< 0, a ₂ = 0 Рис.2e. a ₁> 0, a ₂ = 0 Рис.2f. a ₁< 0, a ₂ = a ₁

Рис.2g. a ₁> 0, a ₂ = a ₁ Рис.2h. a ₁ < a ₂< 0 Рис.2i. a ₁ > a ₂> 0

Наконец, в последних двух случаях, показанных на рис.1 l и 1m – и только в этих случаях – получаем зигзаги, показанные на рис.2h и 2i, подобные представленным рис.1.1.

Таким образом, на рис.2 представлены все возможные варианты графиков игрока А в за-висимости от a ₁ и a ₂.

Перейдём теперь к игроку В и проведём для него аналогичные рассуждения. Для любой стратегии x игрока А положим

y _B(x) = { y | () (g _B(x, y') ≤ g _B(x, y))}. (14b)

Другими сдовами, y _B(x) – это множество всех стратегий y игрока B, которые максимизирует его выигрыш g _B(x, y) при данном x.

Определим график игрока В формулой, аналоничной формуле (16а):

Y _В = {(x, y) | x Î[0, 1], y Î y _B(x)}. (16b)

Повторяя все те рассуждения, которые были сделаны для графика игрока А, применитель-но к графику игрока В, совершенно аналогично приходим к 9 графикам, показанным на рис.3.

Рис.3a. b ₁= 0, b ₂ = 0 Рис.3b. b ₁= 0, b ₂< 0; b ₁> 0, Рис.3c. b ₁= 0, b ₂> 0; b ₂ > b ₁> 0;

b ₂< 0; b ₂< b ₁< 0 b ₁< 0, b ₂> 0

Рис.3d. b ₁< 0, b ₂ = 0 Рис.3e. b ₁> 0, b ₂ = 0 Рис.3f. b ₁< 0, b ₂ = b ₁

Рис.3g. b ₁> 0, b ₂ = b ₁ Рис.3h. b ₁ < b ₂< 0 Рис.3i. b ₁ > b ₂> 0

Из определения равновесия Нэша и формул (14а) и (14b) сразу следует

Утверждение 5. Любая точка (x *, y *), принадлежащая пересечению графиков Φ _Aи Y _В, яв-ляется равновесием Нэша ■

Имеет место утверждение, завершающее построение равновесия Нэша:

Утверждение 6. Длялюбых параметров a ₁, a ₂, b ₁ и b ₂ пересечение графиков Φ _Aи Y _В не-пусто.

Для доказательства утверждения надо рассмотреть все пары графиков, в которых 1-ый график является одним из 9 графиков рис.2, а 2-ой график – одним из 9 графиков рис.3. Заме-тим, что каждый из графиков содержит не менее 2-ух вершин единичного квадрата. Поэтому в случаях, когда один из графиков содержит не менее 3-ёх вершин, пересечение обязательно есть. Таким образом, осталось рассмотреть только случаи, когда каждый из графиков содержит толь-ко две вершины. Это графики на рисунках 2b, 2c, 2h, 2i и на рисунках 3b, 3c, 3h, 3i. Во всех этих 16-и случаях, кроме двух пар: á2h, 3iñ и á2i, 3hñ наличие хотя бы одной общей вершины очевид-но. В последних дух случаях имеется одна внутренняя общая точка, как это показано на рис.11-1.3 ■

Для анализа биматричных игр требуется найти все равновесия Нэша и выигрыши обоих игроков в этих равновесиях. Для этого надо выполнить следующий

Алгоритм 1. Анализ биматричной игры размерности 2×2.

1. По платёжным матрицам А и B обоих игроков, пользуясь формулами (8) и (9), найти па-раметры a ₁, a ₂, b ₁, b ₂.

2. По параметрам a ₁ и a ₂, определить график игрока А, пользуясь рис.2.

3. По параметрам b ₁ и b ₂, определить график игрока B, пользуясь рис.3.

4. Найти пересечение найденных графиков.

5. Для каждой точки (x *, y *) из указанного пересечения, определить смешанные стратегии x = (x *, 1 – x *), y = (y *, 1 – y *). Все они представляют собой искомые равновесия Нэша.

6. Выигрыш игрока А в равновесии Нэша определяется формулой (10а), игрока B– фор-мулой (10b), в которые подставляются координаты x и y данного равновесия (вероятности вы-бора игроками своих 1-ых чистых стратегий). Заметим, что если данное равновесие является равновесием в чистых стратегиях, то ничего вычислять не надо: выигрыши игроков равны соот-ветствующим элементам платёжной матрицы. Например, если равновесием является пара стра-тегий á1, 1ñ, то выигрыш игрока А равен a ₁₁, игрока B– b ₁₁, и т.д.■

Для иллюстрации работы алгоритма 1 рассмотрим несколько примеров.

Пример 4. Рассмотрим игру Аумана из примера 1. Её платёжная матрица задаётся форму-лой (1). В примере 2 было установлено, что в данной игре существует единственное равновесие á2, 2ñ в чистых стратегиях. Это равновесие при записи в виде смешанной стратегии принимает вид x = (0, 1), y = (0, 1). Убедимся, что никаких других равновесий у игры Аумана нет. В данном случае

a ₁₁ = 100, a ₁₂ = 0, a ₂₁ = 101, a ₂₂ = 1;

b ₁₁ = 100, b ₁₂ = 101, b ₂₁ = 0, b ₂₂ = 1.

По формулам (8) и (9) получаем

a ₁ = a ₁₁ – a ₁₂ – a ₂₁ + a ₂₂ = 100 – 0 – 101 + 1 = 0;

a ₂ = a ₂₂ – a ₁₂ = 1 – 0 = 1;

b ₁ = b ₁₁ – b ₁₂ – b ₂₁ + b ₂₂ = 100 – 101 – 0 + 1 = 0;

b ₂ = b ₂₂ – b ₂₁ = 1 – 0 = 1.

График игрока А при a ₁ = 0, a ₂> 0 показан на рис.2c; график игрока B при b ₁ = 0, b ₂> 0 показан на рис.3c. Оба графика и их пересечение показаны на рис.4. Единственной общей точкой явля-ется точка (0, 0), которой и соответствует единственное равновесие Нэша x = (0, 1), y = (0, 1).

Найдём выигрыши игроков. В соответствии с шагом 6 алгоритма 1 имеем g _A(0, 0) = a ₂₂ = 1; g _В(0, 0) = b ₂₂ = 1■

Пример 5. Рассмотрим биматричную игру из примера 3 с платёжной матрицей Q = 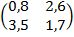, которая не имеет равновесий Нэша в чистых стратегиях. Подсчитаем a ₁, a ₂, b ₁, b ₂поформулам (8), (9):

a ₁ = a ₁₁ – a ₁₂ – a ₂₁ + a ₂₂ = 0 – 2 – 3 + 1 = –4;

a ₂ = a ₂₂ – a ₁₂ = 1 – 2 = –1;

b ₁ = b ₁₁ – b ₁₂ – b ₂₁ + b ₂₂ = 8– 6– 5 + 7 = 4;

b ₂ = b ₂₂ – b ₂₁ = 7 – 5 = 2.

 

Вид графика игрока А при a ₁ = –4, a ₂ = –1 (a ₁ < a ₂< 0) показан на рис.2h; вид графика игрока B при b ₁ = 4, b ₂ = 2 (b ₁ > b ₂> 0) показан на рис.3i. В данном случае y ₀ = 0,25; x ₀ = 0,5. Оба графика и их пересечение показаны на рис.5. Единственной общей точкой графиков является точка (0,5; 0,25), которой и соответствует единственное равновесие Нэша x = (0,5; 0,5), y = (0,25; 0,75).

Выигрыши игроков определяются по формулам (10):

g _A(0,5; 0,25) = –4·0,5·0,25 +1·0,5+ (3– 1) ·0,25+ 1 = –0,5 + 0,5 + 0,5 + 1 = 1,5;

g _B(0,5; 0,25) = 4·0,5·0,25 – 2·0,25 + (6– 7) ·0,5 + 7 = 0,5 – 0,5 – 0,5 + 7 = 6,5 ■

Рис.4. Равновесие в чистых стратегиях.

Рис.5. Равновесие в смешанных стратегиях.

Пример 6. Игра «Семейный спор». Рассмотрим биматричную игру со следующей платёж-ной матрицей Q = . Подсчитаем a ₁, a ₂, b ₁, b ₂поформулам (8), (9):

a ₁ = a ₁₁ – a ₁₂ – a ₂₁ + a ₂₂ = 1 – 0 – 0 + 2 = 3;

a ₂ = a ₂₂ – a ₁₂ = 2 – 0 = 2;

b ₁ = b ₁₁ – b ₁₂ – b ₂₁ + b ₂₂ = 2– 0– 0 + 1 = 3;

b ₂ = b ₂₂ – b ₂₁ = 1 – 0 = 1.

Вид графика игрока А при a ₁ = 3, a ₂ = 2 (a ₁ > a ₂> 0) показан на рис.2i; вид графика игрока B при b ₁ = 3, b ₂ = 1 (b ₁ > b ₂> 0) показан на рис.3i. В данном случае y ₀ = ⅔; x ₀ = ⅓. Оба графика и их пересечение показаны на рис.6. Таким образом, в данной игре есть два равновесия в чистых

Рис.6. Три равновесия.

стратегиях и одно равновесие в смешанных стратегиях. Выигрыши в паре чистых стратегий á1, 1ñ, соответствующей пересечению графиков в точке (1, 1), равны 1 и 2. Выигрыши в паре чис-тых стратегий á2, 2ñ, соответствующей пересечению графиков в точке (0, 0), равны 2 и 1. Нако-нец, выигрыши в паре смешанных стратегий, соответствующей пересечению графиков в точке (⅓,⅔), определяются по формулам (10):

g _A(⅓,⅔) = 3·⅓·⅔ – 2·⅓ + (0– 2)·⅔ + 2 = ⅔ – ⅔ – 2·⅔ + 2 = ⅔;

g _B(⅓,⅔) = 3·⅓·⅔ – 1·⅔ + (0– 1)·⅓ + 1 = ⅔ – ⅔ – ⅓ + 1 = ⅔.

В отличие от примеров 4 и 5, в данном примере имеется 3 равновесия Нэша. Здесь впер-вые в нашем курсе возникает один из центральных вопросов организации коллективного взаи-модействия участников (игроков), который в данном случае формулируется так: какое равнове-сие лучше? В чистых стратегиях имеется два равновесия, в которых один игрок выигрывает 2, а другой 1. Естественно, что игрок А заинтересован в равновесии á2, 2ñ, в котором его выигрыш равен 2, а у игрока В равен 1. По тем же причинам игрок В заинтересован в равновесии á1, 1ñ, в котором его выигрыш равен 2, а у игрока А равен 1. В единственном смешанном равновесии x = (⅓, ⅔), y = (⅔,⅓) выигрыши у обоих игроков равны ⅔,т.е. каждый получает меньше, чем в двух других равновесиях. Но зато они получают поровну, т.е. никто никому не завидует (в от-личие от двух других равновесий), и этот вариант часто представляется более справедливым. Вопрос о том, что лучше – бóльший доход или справедливость – вообще не решается в рамках математики (или любой другой науки). Математика (как в данном случае) позволяет правильно описать имеющиеся возможности. А решение принимается другими людьми на основе других соображений ■

Разумеется, приведённые примеры далеко не исчерпывают всех возможностей в бимат-ричной игре размерности 2×2.В частности, возможно бесконечное множество равновесий Нэ-ша (когда у двух графиков оказывается общим некоторый отрезок). Однако рассуждения и вы-числения в соответствии с алгоритмом 1 позволяют проанализировать (с данной точки зрения) любую игру из рассматриваемого класса игр.

Задание 2. Проанализировать в соответствии с алгоритмом 1 биматричные игры с указан-ными платёжными матрицами. В качестве образца см. примеры 4, 5 и 6.

■

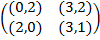
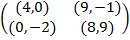
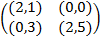
Позиционные игры

Не давая пока никаких формальных определений, рассмотрим примеры игр другого типа, в которых ходы делаются по очереди, каждый ход и каждое новое (после этого хода) состояние игры немедленно становятся известными обоим игрокам.

Пример 7. Игра «ним». В этой игре на стол между двумя игроками выкладывается неко-торое количество фишек. При каждом ходе игрок должен разделить одну из имеющихся групп фишек на дванепустых подмножества разных размеров. Например, 6 фишек можно разделить на группы 5 и 1 или 4 и 2, но не 3 и 3. В начале игры все фишки образуют одну группу. После 1-го деления появится две группы, после 2-го деления – 3 группы, и т.д. Игрок, который не смо-жет больше сделать ход, проигрывает. На рис.7 показан граф игры «ним»для 7 фишек. Каждая вершина этого графа соответствует одному из возможных разбиений 7 фишек на группы. Их можно назвать позициями в игре. Позиция á5-1-1ñ означает, что имеется три группы: в 1-ой группе – 5 фишек, а в двух других – по 1-ой фишке. Дуги соответствуют возможным ходам иг-рока в данной позиции. В позиции á5-1-1ñ есть две возможности: разделить группу из 5 фишек на группы из 3-ёх и 2-ух фишек или на группы из 4-ёх и 1-ой фишки. Это значит, что из пози-ции á5-1-1ñ можно перейти в позиции á3-2-1-1ñ и á4-1-1-1ñ. Позиции á2-2-2-1ñ, á2-2-1-1-1ñ и á2-1-1-1-1-1ñ называются финальными, поскольку из них никуда нельзя перейти. Позиция á7ñ назы-вается начальной.

Рис.7. Граф игры «ним»для 7 фишек ■

Пример 8. Игра«Две кучки». Имеется две кучки, в каждой из которых имеется 4 фишки. Игрок может сделать один из следующих трёх ходов:

1. Забрать одну фишку из 1-ой кучки.

2. Забрать одну фишку из 2-ой кучки.

3. Забрать по одной фишке из обеих кучек.

Два игрока делают ходы по очереди. Проигрывает игрок, который забирает последнюю фишку. Разумеется, если в процессе игры в одной из кучек не осталось фишек, то у игроков из трёх хо-дов остаётся только один: забрать одну фишку из той кучки, в которой они ещё остались.

Рассматриваемую игру можно представить графом, показанным на рис.8. Как и в преды-дущем примере, вершины соответствуют всем возможным позициям в игре, а дуги – ходам, т.е. переходам между позициями. Пара чисел в скобках у вершины указывает на число предметов в 1-й и 2-й кучке в соответствующей позиции. Игра начинается в вершине (4,4) и заканчивается в вершине (0,0). Из каждой вершины есть три перехода – налево (взят предмет из 1-й кучки), вниз (взят предмет из 2-й кучки) и по диагонали (взяты по одному предмету из обеих кучек).

Рис.8. Граф игры «две кучки» ■

 

Дадим теперь достаточно общее описание игр рассматриваемого типа. Имеется ациклич-ный (т.е. не содержащий циклов) граф. Одна вершина объявляется начальной. Одна (отличная от начальной) вершина объявляется финальной. Предполагается, что финальная вершина явля-ется единственной вершиной в графе, из которой не выходит ни одной дуги. Игра состоит в том, что игроки по очереди переходят из вершины в вершину по дугам графа, причём 1-ая вер-шина обязательно должна быть начальной. При указанном предположении через конечное чис-ло ходов один из игроков обязательно попадает в финальную вершину, на чём игра и заканчи-вается. Игрок, попавший в финальную вершину, считается победителем. Обычно (см. примеры 7 и 8) вершины графа интерпретируются как позиции в игре, что и позволило дать таким играм естественное название «позиционные».

На первый взгляд, некоторые условия могут показаться слишком ограничительными. В игре «ним»имеетсяне одна, а три финальных вершины. В ней игрок, попавший в любую фи-нальную вершину, действительно является победителем, поскольку другой игрок не может хо-дить. В то же время в игре «две кучки»игрок, попавший в единственную финальную вершину (0,0), является проигравшим, так как он взял последнюю фишку. Но оказывается, что все эти ситуации просто сводятся к описанной. Рассмотрим эти ситуации по отдельности.

1. Имеется несколько финальных вершин. Добавим к графу одну вершину z и проведём дуги из каждой финальной вершины в вершину z. Вершина z будет единственной финальной вершиной в новом графе. Если в исходной игре попадание в любую финальную вершину было проигрышем, то в новой игре попадание в новую единственную финальную вершину стало вы-игрышем. Наоборот, если в исходной игре попадание в любую финальную вершину было выиг-рышем, то в новой игре попадание в новую единственную финальную вершину стало проигры-шем. Понятно, что суть игры совершенно не изменилась, поскольку в новую вершину попадает всегда не тот игрок, который попал в любую из исходных финальных вершин, а как раз другой. Таким образом, всегда можно рассматривать эквивалентную игру с одним финальным состоя-нием.

2. Игрок, попавший в единственную финальную вершину, считается проигравшим. В этом случае также добавляется одна новая финальная вершина z, в которую ведёт одна дуга из старой финальной вершины. Очевидно, что игрок, не попавший в старую финальную верши-ну, попадает в новую финальную вершину, т.е. является победителем в новой игре. Поэтому проигравшим в новой игре игроком является тот же игрок, который был проигравшим и в ста-рой игре, т.е. новая и старая игра эквивалентны.

Таким образом, мы приходим к описанной выше модели позиционной игры, победитель которой – это игрок, попавший в единственную финальную вершину.

Опишем алгоритм, позволяющий одному из игроков всегда выигрывать в позиционной игре. Суть его в том, что вершинам графа (т.е. позициям игры) приписываются метки 0 или 1. В зависимости от того, какую метку получает начальная вершина, выигрывает начинающий или делающий следующий за ним ход игрок.