Исследование в матричных играх начинается с нахождения её цены. Если матричная игра имеет решение, то нахождением цены игры (и соответствующих оптимальных стратегий) ис-следование игры и заканчивается. Но при нахождении оптимальных стратегий в любом случае определяется нижняя и верхняя цена данной игры (см. формулы (2) и (4)). Игрок A не должен надеяться на выигрыш бóльший, чем верхняя цена игры, и может быть уверен в получении вы-игрыша не меньше нижней цены игры (соответсвенно, игрок B не должен надеяться на проиг-рыш мéньший, чем нижняя цена игры, и может быть уверен, что его проигрыш не больше верх-ней цены игры). В этом общем случае новые решения матричных игр следует искать в возмож-ности многократного повторения игр и применения стратегий случайно, с определённой веро-ятностью.
Модификация исходной матричной игры, в которой её стратегии могут выбираться игро-ками уже не однозначно (как в разделах 1 - 3), а вероятностным образом, называется смешан-ным расширением данной матричной игры. Если игрок A выбирает стратегию i c вероятностью xi (i = 1,..., m), а игрок B- стратегию j c вероятностью yj (j = 1,..., n), то говорят, что игроки A и B используют смешанные стратегии x = (x 1,..., xm) и y = (y 1,..., yn). Стратегии исходной игры обычно называются чистыми стратегиями, а рассмотренные в разделе 2 решения исходной игры - решениями в чистых стратегиях. Чистая стратегия является частным случаем смешан-ной стратегии, когда все вероятности, кроме вероятности выбора данной чистой стратегии, рав-ны 0, а вероятность выбора данной чистой стратегии равна 1.
Таким образом, в смешанном расширение матричной игры множество стратегий игрока A- это бесконечное множество вероятностных распределений на конечном множестве исходных чистых стратегий {1,..., m }. Проще говоря, это множество всех векторов x = (x 1,..., xm), у кото-рых все координаты неотрицательны и их сумма равна 1. Координата xi вектора x является ве-роятностью выбора чистой стратегии i. Аналогично определяется множество стратегий игрока B- множество всех векторов y = (y 1,..., yn), у которых все координаты неотрицательны и их сумма равна 1. В отличие от множеств чистых стратегий, множества смешанных стратегий бес-конечны.
Пусть игроки A и B выбрали стратегии x и y. Тогда средний выигрыш игрока A определяется формулой
g (x, y) = 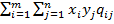 . (9)
. (9)
Как и ранее, игрок A стремится максимизировать свой средний выигрыш g (x, y), а игрок B- ми-нимизировать его, т.е. минимизировать свой средний проигрыш. Как и ранее, игрок A не знает, какую стратегию y выбирает игрок B. Повторяя рассуждения из начала раздела 2, приходим к определению оптимальной смешанной стратегии x * игрока А и нижней цены игры в смешан-ных стратегиях V -:
смешанной оптимальной стратегией x * игрока А называется любая смешанная страте-гия игрока А, на которой достигается внешний максимум по множеству всех смешанных стратегий в следуюшем выражении (максимине):
max x min yg (x, y), (10a) где g (x, y) определяется формулой (9), x * - любая смешанная стратегия игрока А, на которой до-
стигается внешний максимум в (10a) и V - = min yg (x *, y). Обозначим через X * множество всех оптимальных стратегий игрока А. Как и в разделе 2, V - и X * определяются только по платёж-ной матрице Q.
Аналогично определяется минимакс
min y max xg (x, y), (10b)
смешанная оптимальная стратегия y * игрока В, множество Y * всех оптимальных стратегий игрока B и верхняя цена игры в смешанных стратегиях V + = max xg (x, y *), определяемые только по платёжной матрице Q.
Как и в случае чистых стратегий, для смешанных стратегий имеет место неравенство
V - ≤ V +; (11)
если V - = V +, то число V, равное их общему значению, называется ценой игры в смешанных стратегиях.
Решением матричной игры в смешанных стратегиях называется пара стратегий á x *, y *ñ, удовлетворяющая условиям
g (x, y *) ≤ g (x *, y *) ≤ g (x *, y), (12)
где g (x, y) определяется формулой (9), x и y- произвольные стратегии игроков А и B.
Для смешанных стратегий имеет место утверждение, аналогичное утверждению 1 для чис-тых стратегий:
Утверждение 5. 1) V -= V + тогда и только тогда, когда для некоторой пары стратегий á x *, y *ñ выполняются условия (12); 2) стратегии x* и y*, удовлетворяющие (12), являются оптималь-ными; 3) цена игры V = g (x *, y *) ■
Принципиальное отличие случая смешанных стратегий от случая чистых стратегий фор-мулируется в следующем виде:
Утверждение 6. Для любой матричной игры существует решение в смешанных стратеги-ях ■
В частности, в силу утверждений 6 и 5 в любой матричной игре в смешанных стратегиях
V - = V +. (13)
Напомним, что решение игры в чистых стратегиях существует не всегда, что и продемонс-трировано в примере 2.
Пример 5. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей:
Q = 
В этом случае max i min jqij = max{2, 1} = 2; min j max iqij = min{4, 3} = 3, и поскольку
max i min j qij < min j max i qij,
то чистых оптимальных стратегий нет.
Рассмотрим смешанные стратегии x * = (0,75; 0,25) и y* = (0,5; 0,5). Проверим их на опти-мальность. Для этого подсчитаем выражение g (x *, y *). В соответствии с формулой (9) имеем
g (x *, y *) = 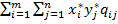 =
= 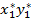 2 +
2 + 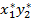 3 +
3 + 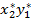 4 +
4 +  1 = 0,75·0,5·2 + 0,75·0,5·3 + 0,25·0,5·4 + 0,25·0,5·1 = 0,75 + 1,125 + 0,5 + 0,125 = 2,5. (14)
1 = 0,75·0,5·2 + 0,75·0,5·3 + 0,25·0,5·4 + 0,25·0,5·1 = 0,75 + 1,125 + 0,5 + 0,125 = 2,5. (14)
Рассмотрим теперь выражение g (x, y *) для произвольной стратегии x = (x 1, x 2). Из 3-его члена в равенствах (14) после простых выкладок получаем
g (x, y *) = x 1·2,5 + x2·2,5 = (x 1 + x2)·2,5 = 2,5 (15a)
(так как сумма вероятностей равна 1).
Рассмотрим теперь выражение g (x *, y) для произвольной стратегии y = (y 1, y 2). Из 3-его члена в равенствах (14) после простых выкладок получаем
g (x *, y) = y 1·2,5 + y 2·2,5 = (y 1 + y2)·2,5 = 2,5 (15b)
(так как сумма вероятностей равна 1).
Формулы (14), (15a) и (15b) влекут для указанных стратегий x * = (0,75; 0,25) и y* = (0,5; 0,5) и для любых стратегий x = (x 1, x 2) и y = (y 1, y 2) двойное неравенство
g (x, y *) ≤ g (x *, y *) ≤ g (x *, y),
совпадающее с (12). Поэтому по определению пара стратегий á x *, y *ñ является решением в сме-шанных стратегиях данной матричной игры, не обладающей решением в чистых стратегиях ■
Пример 6. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей:
Q = 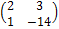
В этом случае max i min jqij = max{2, -14} = 2; min j max iqij = min{2, 3} = 2, и поскольку макси-мин равен минимаксу, пара чистых стратегий á1, 1ñ является решением данной игры в чистых стратегиях (см. раздел 2).
Напомним, что чистая стратегия является частным случаем смешанной. Положим x * = (1; 0) и y* = (1; 0). Пара смешанных стратегий á x *, y *ñ является той же самой парой чистых стра-тегий á1, 1ñ. При этом, с учётом матрицы Q и вида стратегий x * и y *, имеем
g (x *, y *) = 2. (16)
Рассмотрим теперь выражение g (x, y *) для произвольной стратегии x = (x 1, x 2). В данном случае, с учётом матрицы Q и того, что y* = (1; 0), получаем
g (x, y *) = x 1·2 + x 2·1 = x 1·2 + (1 -x 1) = x 1+1 ≤ 2. (17a)
Аналогично, для x * = (1; 0) и произвольной стратегии y = (y 1, y 2), получаем
g (x *, y) = y 1·2 + y 2·3 = y 1·2 + (1 -y 1)·3 = 3 -y 1³ 2. (17b)
Формулы (16), (17a) и (17b) влекут для указанных стратегий x * = (0,75; 0,25) и y* = (0,5; 0,5), и для любых стратегий x = (x 1, x 2) и y = (y 1, y 2) двойное неравенство
g (x, y *) ≤ g (x *, y *) ≤ g (x *, y),
совпадающее с (12). Поэтому по определению исходная пара чистых стратегий á x *, y *ñ, которая была решением данной игры в чистых стратегиях, является решением этой же игры и в смешанных стратегиях ■
Результат примера 6 не случаен. Имеет место (почти очевидное)
Утверждение 7. В любой матричной игре решение в чистых стратегиях является решени-ем в смешанных стратегиях ■
К сожалению, поиск решений матричных игр в смешанных стратегиях (если у них нет решений в чистых стратегиях) является достаточно сложным с вычислительной точки зрения и здесь не рассматривается. Однако для отдельных классов матричных игр удаётся найти реше-ния в смешанных стратегиях значительно более простыми способами, которые рассматривают-ся в следующем разделе.






