Таблица 4.5. Результат итерации 5
| № | |||||||||||||||||||||
| −3 | −4 | ||||||||||||||||||||
| −4 | −1 | ||||||||||||||||||||
| −1 | −5 | −2 | |||||||||||||||||||
Шаг F. Найдём сами кратчайшие пути, используя правые клетки в ячейках. Напомним, что число в правой клетке в ячейке (i, j) – это номер вершины, предшествующей на кратчайшем пути из i в j вершине j, т.е. номер предпоследней вершины на этом пути.
Для пути из 1 в 2 такой вершиной является вершина 3 (см. таблицу 4.5); далее, для пути из 1 в 3 такой вершиной является вершина 4; для пути из 1 в 4 такой вершиной является вершина 5; наконец, для пути из 1 в 5 такой вершиной является вершина 1. Таким образом, кратчайший путь из вершины 1 в вершину 2 таков: 1→5→4→3→2. По построению, все промежуточные пу-ти: 1→5→4→3; 1→5→4; 1→5 также являются не только кратчайшими путями, но и именно те-ми кратчайшими путями, которые найдены данным алгоритмом. Все кратчайшие пути из вер-шины 1 уже найдены. Они таковы: 1→5→4→3→2; 1→5→4→3; 1→5→4; 1→5.
Далее, рассмотрим пути из вершины 2 в другие вершины. На пути из 2 в 1 предпоследней вершиной является вершина 4, а непосредственно перед ней – начальная вершина 2, и весь путь таков: 2→4→1. Далее, на пути из 2 в 3 предпоследней вершиной является 4, и путь таков: 2→4 →3. Путь из 2 в 4 состоит из одной дуги 2→4. Наконец, на пути из 2 в 5 предпоследней верши-ной является 1, а путь из 2 в 1 уже известен, поэтому имеем кратчайший путь 2→4→1→5. Все кратчайшие пути из вершины 2 таковы: 2→4→1; 2→4→3; 2→4; 2→4→1→5.
Кратчайшие пути из вершины 3 таковы: 3→5→4→1; 3→2; 3→5→4; 3→5.
Кратчайшие пути из вершины 4 таковы: 4→1; 4→3→2; 4→3; 4→1→5.
Кратчайшие пути из вершины 5 таковы: 5→4→1; 5→4→3→2; 5→4→3; 5→4 ■
3.1. Циклы отрицательной длины. В АФУ предполагалось, что в заданном графе отсутс-твуют циклы отрицательной длины. При обосновании АФУ это требование существенно, так как само разбиение пути, проходящего через вершину k, на два пути, не содержащих k в качест-ве промежуточной вершины, возможно только при единственном вхождении k в путь, что, в свою очередь, гарантируется как раз отсутствием циклов отрицательной длины. Поскольку в достаточно сложных случаях сам факт наличия или отсутствия таких циклов не является оче-видным, необходим специальный алгоритм, устанавливающий этот факт. Более того, в некоторых практически важных задачах (см. главу 9) требуется найти цикл отрицательной длины или установить их отсутствие безотносительно к нахождению кратчайших путей.
Оказывается, что решение этой проблемы является «побочным продуктом» АФУ. Подроб-нее. Применяем АФУ к произвольному графу, не выясняя заранее, содержит ли он циклы отрицательной длины. Для этого после каждого шага, начиная с 1-го (k =1), проверяем все числа на диагонали матрицы D (напомним, что после инициализации все они равны 0). Пусть хотя бы один элемент (скажем, dii) оказывается меньше 0. Тогда путь с концом в вершине i, найден-ный так же, как и приведённый сразу после описания АФУ способ нахождения кратчайшего пути в вершину i, окажется циклом с началом и концом в вершине i, длина которого равна от-рицательному числу dii. Это следует просто из описания алгоритма, который на каждом k- о м шаге находит текущие кратчайшие пути для всех пар вершин (включая пары с совпадающими
вершинами)
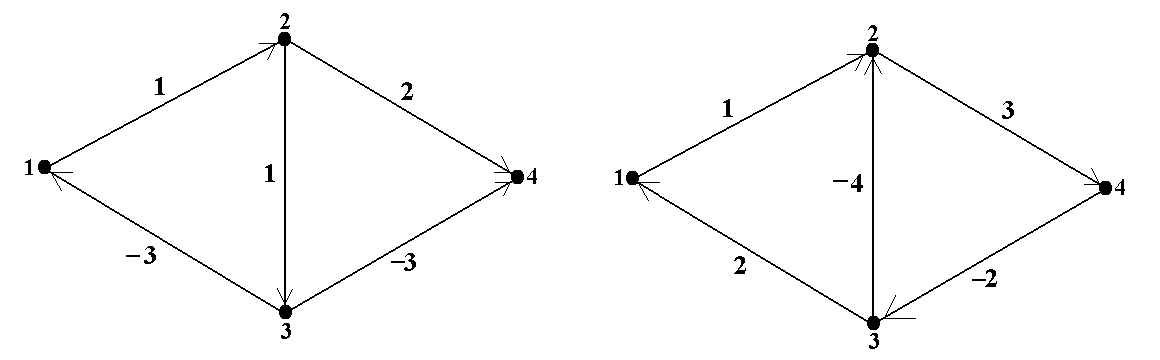
| Пример 4. Проиллюстрируем работу АФУ на примере графа, показанного на рис. 4. В нём есть цикл 3→1→2→3 отрицательной длины −1.Всоответствии с описанием «руч-ной» версии АФУ в примере 3, в результате инициализации получим таблицу 5. Далее, на итерации 1 из таблицы 5 получаем преобразо-ванную таблицу 5.1 точно так же, как это дела-лось в примере 3, а затем точно так же полу-чаем таблицы 5.2 и 5.3. После выполнения итерации 3 обнаружи-ваем путь из вершины 1 в ту же самую верши-ну 1, на котором предпоследней вершиной яв- |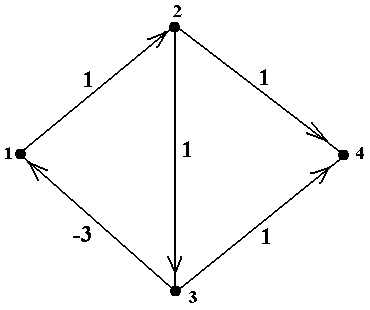 
Рис. 4. Граф с отрицательным циклом
|
ляется вершина 3, перед ней – вершина 2, а перед вершиной 2 – опять вершина 1. Таким обра-зом, найден цикл 1→2→3→1; длина этого цикла, указанная в средней клетке ячейки (1, 1), рав-на −1, т.е. найден цикл отрицательной длины. Разумеется, одновременно найдены циклы2→3
→1→2 и 3→1→2→3, отличающиеся от цикла 1→2→3→1 только начальной вершиной; их
длина также равна −1.
Таблица 5. Результаты инициализации
| № | |||||||||||||||||
| ∞ | ∞ | ||||||||||||||||
| ∞ | |||||||||||||||||
| −3 | ∞ | ||||||||||||||||
| ∞ | ∞ | ∞ | |||||||||||||||
Таблица 5.1. Результат итерации 1
| № | |||||||||||||||||
| ∞ | ∞ | ||||||||||||||||
| ∞ | |||||||||||||||||
| −3 | −2 | ||||||||||||||||
| ∞ | ∞ | ∞ | |||||||||||||||
Таблица 5.2. Результат итерации 2
| № | |||||||||||||||||
| ∞ | |||||||||||||||||
| −3 | −2 | −1 | −1 | ||||||||||||||
| ∞ | ∞ | ∞ | |||||||||||||||
Таблица 5.3. Результат итерации 3
| № | |||||||||||||||||
| −1 | |||||||||||||||||
| −2 | −1 | ||||||||||||||||
| −4 | −3 | −2 | −2 | ||||||||||||||
| ∞ | ∞ | ∞ | |||||||||||||||
■
Таким образом, АФУ позволяет не только установить факт наличия или отсутствия цик-лов отрицательной длины, но и найти по крайней мере один из них.
Задание 2. Используя АФУ, в заданном ориентированном графе найтикратчайшие пути между всеми парами вершин, если циклы отрицательной длины не существуют, или найти такой цикл. Для образца см. примеры 3 и 4.
01 02
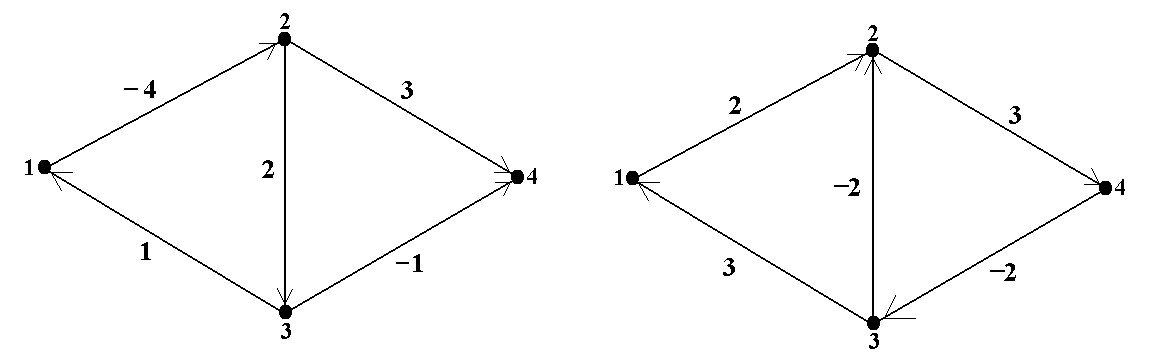
03 04
05 06
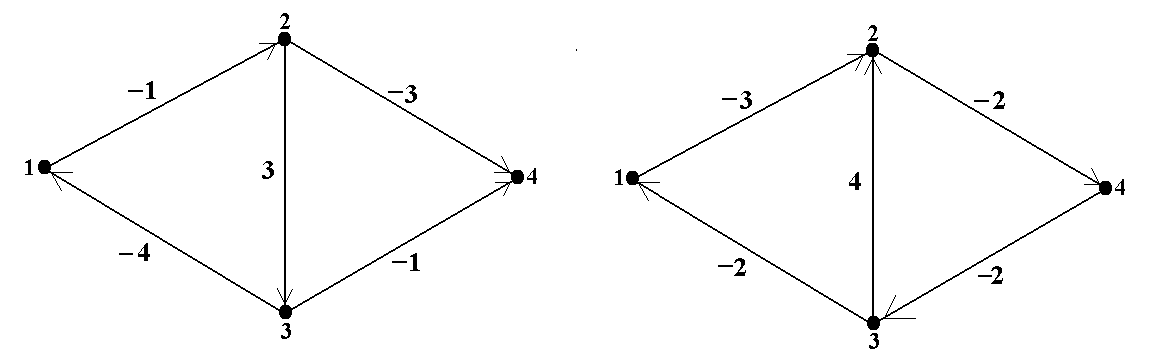
07 08
09 10
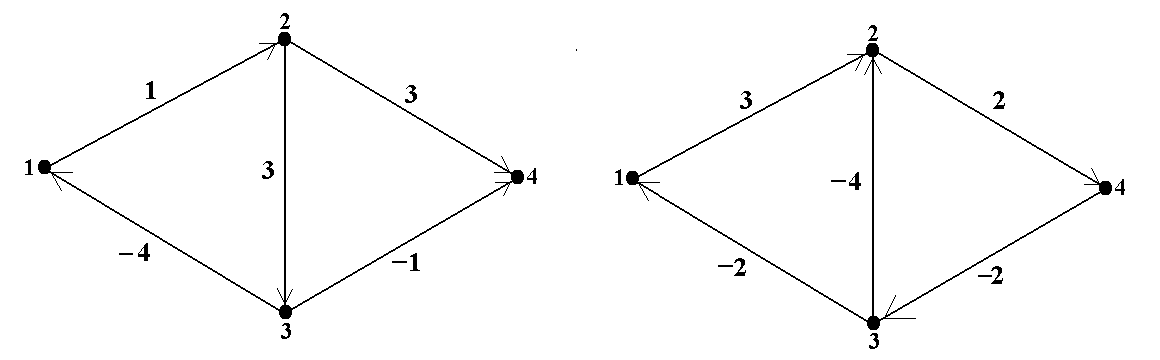
11 12
13 14
15 16
17 18
19 20
■
Замечание. Рассмотренный алгоритм находит кратчайшие пути и циклы отрицательной длины в ориентированном графе. Однако этот же самый алгоритм находит соответствующие пути и циклы в неориентированном графе (см. все определения в разделе 6-3). Просто в описа-нии алгоритма надо все упоминаемые там дуги заменить рёбрами. Например, l (c, x) обозначает длину ребра (c, x) с концами c и x.
