Максимальным называется паросочетание, содержащее максимально возможное число рё-бер. Известно несколько различных методов поиска максимального паросочетания в заданном двудольном графе. Здесь будет рассмотрен потоковый метод построения максимального паро-сочетания. Идея метода такова.
1. По исходному двухполюсному графу строится потоковая сеть (см. главу 7). Для этого добавляется две вершины, которых не было в исходном графе – источник s и сток t. В каждую вершину 1-ой доли входит одна новая дуга, выходящая из источника. Из каждой вершины 2-ой доли выходит одна новая дуга, входящая в сток. Все «старые» рёбра графа ориентируются в направлении от 1-ой доли к 2-ой доле (напомним, что в исходном графе любое ребро соединяло две разные доли). Положим пропускные способности всех дуг построенной сети равными 1. Таким образом, потоковая сеть полностью определена.
2. Найдём алгоритмом Форда-Фалкерсона (АФФ) максимальный поток в построенной се-ти. В силу утверждения 7-7 все компоненты потока – целые числа. А поскольку пропуск-ные способности всех дуг равны 1, то отсюда следует, что поток в любой дуге равен либо 0, ли-бо 1.
3. Рассмотрим все дуги, выходящие из 1-ой доли и входящие во 2-ую долю, в которых по-токи равны 1. Если хотя бы две таких дуги выходят из одной и той же вершины, то в силу «за-кона сохранения» (сумма потоков во всех входящих в вершину дугах равна сумме потоков во всех выходящих из вершины дугах) сумма потоков во входящих дугах не меньше 2. Но в лю-бую вершину 1-ой доли по построению входит только одна дуга, поток в которой не может быть больше 1. Полученное противоречие доказывает, что все дуги, поток в которых равен 1, выходят из разных вершин. Совершенно аналогично доказывается, что все дуги, поток в кото-рых равен 1, входят в разные вершины.
4. Поскольку все рассмотренные дуги, потоки в которых равны 1, не имеют общих кон-цов, то соответствующие им в исходном двудольном графе рёбра образуют паросочетание. Лег-ко понять, что из максимальности потока следует максимальность построенного по нему ука-занным образом паросочетания. Действительно, если найденное паросочетание не является максимальным, то существует паросочетание с бóльшим числом рёбер. По этому новому паро-сочетанию построим поток, величина которого будет равна числу рёбер в нём. Но это значит, что его величина больше величины максимального потока, что невозможно. Это и доказывает максимальность построенного ранее паросочетания.
Пример 1. Проиллюстрируем введённые понятия и рассуждения. Рассмотрим двудольный граф, показанный на рис.6-32. Этот же граф показан здесь на рис.1. Построенная по нему описанным выше образом потоковая сеть S показана на рис.2. Найденный с помощью АФФ максимальный поток в сети S условно показан на рис.3. Жирным выделены все дуги, потоки в которых равны 1; потоки во всех остальных дугах равны 0. Таким образом, максимальное паро-сочетание в исходном двудольном графе на рис.1 состоит из следующих рёбер: (1, 8), (3, 9), (4, 7), (5, 10), (6, 11). Число рёбер в максимальном паросочетании равно 5. Без сложных рассужде-ний легко понять, что это число не может превосходить 5, поскольку 1-ая доля содержит только
Рис.1. Исходный двудольный граф
Рис.2. Сеть, построенная по графу
Рис.3. Максимальный поток в сети
5 вершин, которые могут быть соединены с вершинами из 2-ой доли. Однако даже в этом прос-том случае не так просто «увидеть глазами» паросочетание, содержащее 5 рёбер ■
Таким образом, описанный подход позволяет решить простейшую из рассматриваемых в курсе задач на паросочетания – задачу поиска максимального паросочетания.
Задание 1. Представить данный двудольный граф в виде потоковой сети; найти с по-мощью АФФ максимальный поток в полученной сети; поток представить графически, как на рис.3, и указать максимальное паросочетание в виде перечня его рёбер. Для образца использовать пример 1 и пример 7-7.
01 02
03 04
05 06
07 08
09 10
11 12
13 14
15 16
■
Задача назначения
Естественным обобщением рассмотренной в разделе 1 задачи поиска максимального па-росочетания является задача поиска максимального взвешенного паросочетания. Суть дела в том, что каждому ребру заданного двудольного графа сопоставлено некоторая положительное число – вес ребра. Рассматриваемая задача состоит в поиске паросочетания с максимальным суммарным весом. Легко понять, что рассмотренная в разделе 1 задача является частным случа-ем последней задачи, когда веса всех рёбер равны 1.
Во многих случаях вершины 1-ой доли интерпретируются как исполнители, вершины 2-ой доли – как работы, а наличие соединяющего их ребра с весом a – как возможность выполнения данной работы данным исполнителем с эффективностью (доходом) a. При такой интерпретации задача поиска максимального взвешенного паросочетания представляет собой поиск такого рас-пределения задач по исполнителям, при котором суммарная эффективность будет максималь-ной. Именно поэтому рассматриваемая задача чаще называется задачей назначения (работ ис-полнителям). Настоящий раздел и посвящён этой задаче.
Прежде чем двигаться дальше, сформулируем утверждение, связывающее циклы и паро-сочетания в произвольных двудольных графах.
Пусть G (V, E)– двудольный граф, V = X 
Y, где X и Y – множества вершин первой и вто-рой доли графа G, С – произвольный цикл в графе G. Нетрудно понять, что число рёбер в лю-бом цикле двудольного графа чётно. Обозначим через С 1 множество рёбер цикла, взятых через одно, а через С 2 – множество остальных рёбер этого цикла (также взятых через одно). Пусть P – произвольное паросочетание в графе G. Определим множество рёбер P’ следующим образом:
P’ = (P 
С 1) С 2. (1)
Имеет место
Утверждение 1. Для любого паросочетания P и любого цикла C множество P’ также явля-ется паросочетанием.
Утверждение 1 почти очевидно. Действительно, при удалении ребра из цикла и добавле-нии следующего ребра число инцидентных их общей вершине рёбер останется равным 1. Поэтому новое множество рёбер останется паросочетанием ■
Каждому ребру (v, w) графа G сопоставлен неотрицательный вес с (v, w) ≥ 0. Задачей о максимальном взвешенном паросочетании в двудольном графе G называется задача нахожде-ния в нём паросочетания, суммарный вес рёбер которого максимален.
Алгоритм решения этой задачи, как и большинства других задач оптимизации на графах, состоит в последовательном переходе от одних паросочетаний к другим, с бóльшим суммарным весом (т.е. к лучшим с рассматриваемой точки зрения), до тех пор, пока не будет достигнуто решение. Ниже будет описан один этап алгоритма – переход от произвольного паросочетания к следующему.
Алгоритм 1 улучшения заданного паросочетания. Исходное паросочетание P состоит из рёбер (x 1, y 1), (x 2, y 2), …, (xn, yn).
1. По заданному двудольному графу G и паросочетанию P построим ориентированный взвешенный граф G * следующим образом:
· множество вершин графа G * совпадает с множеством вершин графа G;
· каждое ребро (xk, yk) Î P определяет дугу (xk, yk) графа G * с тем же весом с (xk, yk), каким обладает ребро (xk, yk) в исходном графе;
· каждое ребро (xk, yk) Ï P определяет дугу (yk, xk) графа G * с весом − с (xk, yk).
2. С помощью алгоритма Флойда-Уоршолла находим в графе G * орцикл отрицательной стоимости (если таковой существует). Отсутствие орциклов в графе G * означает, что исходное взвешенное паросочетание P максимально. Алгоритм улучшения прекращает работу.
3. Разобьём множество дуг найденного орцикла С на два подмножества С 1 и С 2, где все дуги, принадлежащие С 1, ведут из X в Y, а все дуги, принадлежащие С 2, ведут из Y в X. Более того, если перейти от дуг (отменой ориентации) обратно к рёбрам G, то, по построению, все рёбра из С 1 содержатся в исходном паросочетании P, а все рёбра из С 2 не содержатся в нём. Также по построению, веса всех дуг из С 1 совпадают с исходными весами дуг в графе G, а веса всех дуг из С 2 равны исходным весам со знаком −. Поскольку сумма весов во всех дугах цикла отрицательна, то это означает, что в исходном графе сумма весов у всех дуг, входящих в мно-жество С 2, строго больше, чем сумма весов во всех дугах, входящих в множество С 1.
4. Рассмотрим цикл С в исходном графе G, и два его подмножества чередующихся рёбер С 1 и С 2, которые были определены на шаге 3. Определим по исходному паросочетанию P и множествам рёбер С 1 и С 2 новое паросочетание P’ формулой (1):
P’ = (P С 1) С 2.
На шаге 3 было отмечено, что все рёбра из С 1 входят в P, а все рёбра из С 2 не входят в P. Так как суммарный вес всех дуг, входящих в С 2, по построению строго больше, чем суммарный вес всех дуг, входящих в С 1, то ровно настолько же вес нового паросочетания P’ больше, чем вес исходного паросочетания P. Таким образом, новое паросочетание имеет бóльший вес, чем ис-ходное ■
Алгоритм построения максимального взвешенного паросочетания сводится к двум шагам. На 1-ом шаге строится начальное паросочетание (например, потоковым алгоритмом из раздела 1). 2-ой шаг состоит в многократном применении только что описанного алгоритма 1 – до тех пор, пока на шаге 2 этого алгоритма будет установлено отсутствие циклов отрицательной длины.
Пример 2. Проиллюстрируем алгоритм построения максимального взвешенного паросо-четания. Исходный взвешенный двудольный граф G показан на рис.4.1. Веса рёбер указаны ря-
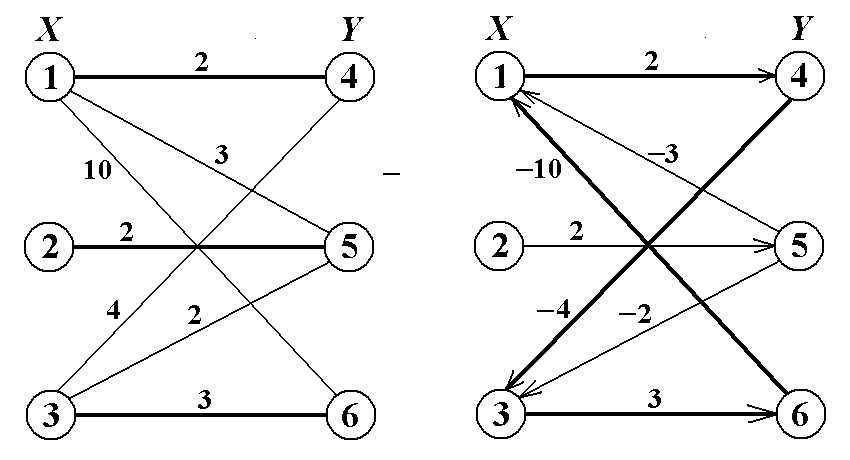
Рис.4.1 Рис.4.2
ом с ними; номера вершин указаны в кружках. Рёбра начального паросочетания P = {(1,4), (2,5), (3,6)} на рис.4.1 выделены. Вес выделенного паросочетания равен 7.
На рис.4.2 показан построенный по исходному паросочетанию P орграф G *. В соответст-вии с алгоритмом 1 все рёбра исходного паросочетания превращаются в дуги с положительными
весами, ориентированные от доли X к доле Y, а все остальные рёбра превращаются в дуги с отрицательными весами, ориентированные от доли Y к доле X. В графе G * существует орцикл 1→4 →3→6→1 с отрицательным весом 2 – 4 + 3 – 10 = – 9. В этом цикле С 1 = {(1,4), (3,6)}, С 2 = {(6,1), (4,3)}. Возвращаясь к исходному графу и отменяя ориентации, получаем С 2 = {(1,6), (3, 4)}.
Далее, в соответствии с формулой (1), получим новое паросочетание P’ = (P С 1) С 2 = ({(1,4), (2,5), (3,6)} 
{(1,4), (3,6)}) 
{(1,6), (3,4)} = {(2,5), (1,6), (3,4)} (см. определения и алгоритмы выполнения теоретико-множественных операций в разделе 2-3). Это новое паросо-четание выделено на рис.4.3. Строя по нему орраф G *, как указано на шаге 1 алгоритма 1, при-ходим к орграфу, показанному на рис.4.4.
Рис.4.3 Рис.4.4
Можно непосредственно убедиться (не прибегая к помощи алгоритма Флойд-Уоршолла), что в последнем орграфе орциклы отрицательной длины отсутствуют. Поэтому последнее паро-сочетание, показанное на рис.4.3, будет максимальным. Его вес равен 16. Оно превосходит вес (7) предыдущего паросочетания на 9 – в соответствии с теорией, как раз настолько, насколько сумма весов рёбер из множества С 2 = {(1,6), (3,4)}, равная 14, больше суммы весов рёбер из множества С 1 = {(1,4), (3,6)}, равной 5 ■
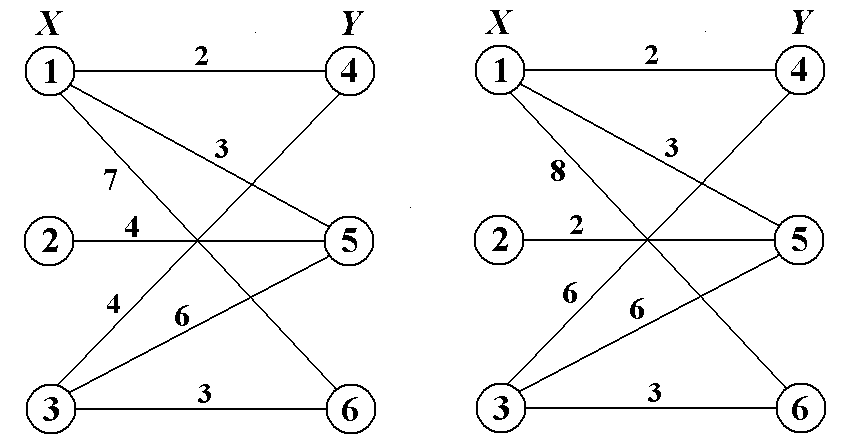
Задание 2. В следующих взвешенных двудольных графах найти максимальные взвешен-ные паросочетания. В качестве образца использовать пример 2.
01 02
03 04
05 06
07 08
09 10
11 12
13 14
15 16
■
Предметный указатель
Назначения, задача
Паросочетание,
взвешенное
максимальное
