График функции  называется выпуклым на интервале
называется выпуклым на интервале 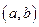 , если он расположен ниже любой своей касательной, проведенной в любой точке этого интервала. График функции
, если он расположен ниже любой своей касательной, проведенной в любой точке этого интервала. График функции  называется вогнутым, интервале
называется вогнутым, интервале 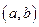 , если он расположен выше любой своей касательной, проведенной в любой точке этого интервала. Точка
, если он расположен выше любой своей касательной, проведенной в любой точке этого интервала. Точка  графика функции, отделяющая его выпуклую часть от вогнутой части, называется точкой перегиба.
графика функции, отделяющая его выпуклую часть от вогнутой части, называется точкой перегиба.
Достаточные условия выпуклости (вогнутости) графика функции. Если  в интервале
в интервале 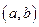 , то график функции является выпуклым в этом интервале. Если
, то график функции является выпуклым в этом интервале. Если  , то в этом интервале график функции вогнутый.
, то в этом интервале график функции вогнутый.
В точке перегиба графика функции вторая производная равна нулю или не существует. Точки, в которых вторая производная равна нулю или не существует, называются критическими точками второго рода. Если 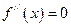 в некоторой точке
в некоторой точке  , бесконечна или вовсе не существует и
, бесконечна или вовсе не существует и  меняет знак при переходе через точку
меняет знак при переходе через точку  , то график функции в точке
, то график функции в точке  имеет перегиб. Если
имеет перегиб. Если  сохраняет знак, то перегиба нет.
сохраняет знак, то перегиба нет.
Найти интервалы выпуклости и точки перегиба функции:
1.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; очки перегиба
; очки перегиба  .
.
2. 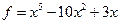 .
.
Ответ: выпукла на  ;
;
вогнута на 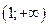 ; точка перегиба
; точка перегиба  .
.
3.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точек перегиба нет.
; точек перегиба нет.
4.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точки перегиба
; точки перегиба  .
.
5.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точка перегиба
; точка перегиба  .
.
6.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точка перегиба
; точка перегиба  .
.
7.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точки перегиба
; точки перегиба  .
.
8.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точки перегиба
; точки перегиба  .
.
9.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точки перегиба
; точки перегиба  ,
,  .
.
10.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точки перегиба
; точки перегиба  .
.
11.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точки перегиба
; точки перегиба  .
.
12.  .
.
Ответ: выпукла на  ;
;
вогнута на  ; точки перегиба
; точки перегиба  .
.
13.  .
.
Ответ: выпукла на  ;
;
вогнута на 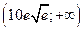 ; точки перегиба
; точки перегиба  .
.
14. 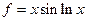 .
.
Ответ: выпукла на  ;
;
вогнута на  ; точки перегиба
; точки перегиба  .
.
15.  . Ответ: выпукла на
. Ответ: выпукла на  ;
;
вогнута на  ; точек перегиба нет.
; точек перегиба нет.
16.  . Ответ: выпукла на
. Ответ: выпукла на  ;
;
вогнута на  , точка перегиба
, точка перегиба  .
.
17. 
 . Ответ: точка перегиба
. Ответ: точка перегиба  .
.
18. 
 . Ответ: точка перегиба
. Ответ: точка перегиба 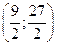 .
.
19. 
 . Ответ: точка перегиба
. Ответ: точка перегиба  .
.
20. При каких значениях параметра  функция
функция  имеет точки перегиба? Ответ:
имеет точки перегиба? Ответ:  .
.
21. Доказать, что график функции  имеет точки перегиба, лежащие на одной прямой.
имеет точки перегиба, лежащие на одной прямой.
22. Доказать, что точки перегиба графика функции  лежат на кривой
лежат на кривой  .
.
23. Может ли точка перегиба функции быть ее точкой экстремума?
24. Может ли всюду выпуклая (вогнутая) функция иметь более одного экстремума?
Доказать неравенство:
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29. 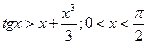 .
.
30.  .
.
31.  .
.
Асимптоты кривой
Пусть для функции 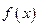 существует такая прямая, что расстояние от точки
существует такая прямая, что расстояние от точки  графика функции до этой прямой стремится к нулю при бесконечном удалении точки
графика функции до этой прямой стремится к нулю при бесконечном удалении точки  о начала координат. Такая прямая называется асимптотой графика функции.
о начала координат. Такая прямая называется асимптотой графика функции.
Если  или
или  , то прямая
, то прямая  является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 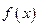 .
.
Если существует конечный предел  , то прямая с уравнением
, то прямая с уравнением 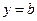 является горизонтальной производной графика функции.
является горизонтальной производной графика функции.
Прямая  является наклонной асимптотой графика функции, если существуют конечные пределы вида
является наклонной асимптотой графика функции, если существуют конечные пределы вида  ,
,  . Если хотя бы один из указанных пределов не существует или равен бесконечности, то у функции наклонных асимптот нет.
. Если хотя бы один из указанных пределов не существует или равен бесконечности, то у функции наклонных асимптот нет.
Если функция задана параметрически  то исследуют, нет ли таких значений параметра
то исследуют, нет ли таких значений параметра  , при которых функции
, при которых функции  или одна из них обращается в бесконечность.
или одна из них обращается в бесконечность.
Уравнение наклонной асимптоты имеет вид  , где
, где  ,
,  , причем
, причем  .
.
Если при 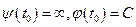 , то график функции имеет вертикальную асимптоту
, то график функции имеет вертикальную асимптоту  . Если при
. Если при  , то график функции имеет горизонтальную асимптоту
, то график функции имеет горизонтальную асимптоту  .
.
Если кривая задана уравнением  в полярной системе координат, то преобразовав уравнение кривой к параметрическому виду по формулам
в полярной системе координат, то преобразовав уравнение кривой к параметрическому виду по формулам  ее асимптоты находят по предыдущему правилу.
ее асимптоты находят по предыдущему правилу.
Если функция задана неявно уравнением  , то для отыскания асимптот в ряде случаев удобнее представить ее в полярных координатах или перейти к параметрическому виду.
, то для отыскания асимптот в ряде случаев удобнее представить ее в полярных координатах или перейти к параметрическому виду.
Пример 1. Найти асимптоты графика функции 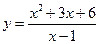 .
.
Решение: При  функция терпит разрыв, причем
функция терпит разрыв, причем  ,
, 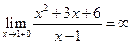 . Значит, прямая
. Значит, прямая  является вертикальной асимптотой. Находим параметры
является вертикальной асимптотой. Находим параметры  наклонной асимптоты
наклонной асимптоты  ,
,  . Следовательно, уравнение наклонной асимптоты имеет вид
. Следовательно, уравнение наклонной асимптоты имеет вид  .
.
Пример 2. Найти асимптоты графика функции  .
.
Решение: Так как  , то прямые
, то прямые  и
и  будут вертикальными асимптотами. Так как при
будут вертикальными асимптотами. Так как при  предел
предел  , то прямая
, то прямая  является горизонтальной асимптотой. Наклонных асимптот нет, так как
является горизонтальной асимптотой. Наклонных асимптот нет, так как  и
и  .
.
Пример 3. Найти асимптоты графика функции  .
.
Решение: Функция не определена в точке 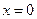 . Но существует предел
. Но существует предел  . Бесконечных разрывов нет. Точка
. Бесконечных разрывов нет. Точка 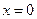 - устранимая точка разрыва. Вертикальных асимптот нет.
- устранимая точка разрыва. Вертикальных асимптот нет.
Определим наклонные асимптоты:
 ,
,  , следовательно,
, следовательно,  будет горизонтальной асимптотой.
будет горизонтальной асимптотой.
Данная кривая бесчисленное множество раз пересекает свою асимптоту  , переходя с одной ее стороны на другую в точках
, переходя с одной ее стороны на другую в точках  ,
,  и неограниченно приближается к ней.
и неограниченно приближается к ней.
Пример 4. Найти асимптоты графика функции 
Решение: При  . Следовательно,
. Следовательно,  является горизонтальной асимптотой. При
является горизонтальной асимптотой. При 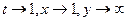 , следовательно,
, следовательно,  есть вертикальная асимптота.
есть вертикальная асимптота.
Пример 5. Найти асимптоты графика функции 
Решение: При  функция стремится к бесконечности.
функция стремится к бесконечности.
 ,
,  ,
,
 ,
,
Следовательно, наклонные асимптоты имеют вид  ,
,  .
.
Пример 6. Найти асимптоты графика функции  .
.
Решение: Приведем уравнение, заданное в полярных координатах, к параметрическому виду:  где
где  - параметр. При
- параметр. При  . Следовательно, график функции имеет горизонтальную асимптоту
. Следовательно, график функции имеет горизонтальную асимптоту 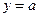 .
.
Найти асимптоты графика функций:
1. 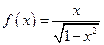 . Ответ: вертикальные асимптоты
. Ответ: вертикальные асимптоты  .
.
2.  . Ответ:
. Ответ: 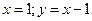 .
.
3.  . Ответ:
. Ответ:  .
.
4.  . Ответ:
. Ответ:  ;
; 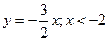 .
.
 (часть гиперболы
(часть гиперболы  ).
).
5.  . Ответ:
. Ответ: 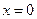 .
.
6.  . Ответ: нет.
. Ответ: нет.
7.  . Ответ:
. Ответ: 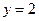 .
.
8.  . Ответ:
. Ответ: 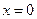 ;
;  при
при  ;
;  при
при 
9.  . Ответ:
. Ответ:  .
.
10.  . Ответ:
. Ответ:  при
при  .
.
Найти асимптоты функции, обратной к функции 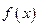 :
:
11.  . Ответ:
. Ответ: 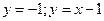 .
.
12.  . Ответ:
. Ответ:  .
.
13.  . Ответ:
. Ответ:  .
.
14.  . Ответ:
. Ответ:  .
.
15  . Найти все асимптоты кривой:
. Найти все асимптоты кривой: 
Ответ:  , точка самопересечения
, точка самопересечения 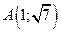 .
.
16  .
.  Ответ:
Ответ: 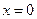 при
при  ;
;  при
при  .
.
17. Может ли график функции иметь две разные асимптоты при  ?
?




