Производной
Геометрически производная  функции
функции 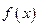 представляет угловой коэффициент
представляет угловой коэффициент  касательной к графику этой функции в точке
касательной к графику этой функции в точке  .
.
Если на плоскости задана точка 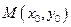 и кривая как график явной функции
и кривая как график явной функции  то:
то:
 - уравнение касательной в точке с абсциссой
- уравнение касательной в точке с абсциссой  ,
,
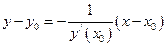 ,
,  - уравнение нормали в точке с абсциссой
- уравнение нормали в точке с абсциссой  . Если
. Если  , то уравнения касательной и нормали имеют вид соответственно:
, то уравнения касательной и нормали имеют вид соответственно:  ,
,  .
.
При параметрическом задании кривой  уравнения касательной и нормали записываются соответственно:
уравнения касательной и нормали записываются соответственно:
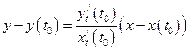 ,
,  ,
,
 ,
,  .
.
Угол между кривыми  и
и  в точке их пересечения
в точке их пересечения  – это угол между касательными к этим кривым в точке
– это угол между касательными к этим кривым в точке  . Этот угол находится по формуле:
. Этот угол находится по формуле:  .
.
Если в точке  производная не определена, но функция имеет различные односторонние пределы
производная не определена, но функция имеет различные односторонние пределы  и
и  , то в этой точке графика функции существуют две различные с соответствующими угловыми коэффициентами
, то в этой точке графика функции существуют две различные с соответствующими угловыми коэффициентами 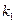 ,
,  односторонние касательные, составляющие угол, а точка называется угловой.
односторонние касательные, составляющие угол, а точка называется угловой.
Если 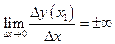 , т.е. функция имеет бесконечную производную, то она не дифференцируема в этой точке. В этом случае график функции имеет вертикальную касательную (точка перегиба).
, т.е. функция имеет бесконечную производную, то она не дифференцируема в этой точке. В этом случае график функции имеет вертикальную касательную (точка перегиба).
Если в точке  функция имеет бесконечные односторонние производные разных знаков, то график функции имеет две слившиеся вертикальные касательные (асимптоты).
функция имеет бесконечные односторонние производные разных знаков, то график функции имеет две слившиеся вертикальные касательные (асимптоты).
Если при прямолинейном движении точки задан закон движения  , то скорость движения в момент
, то скорость движения в момент 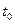 есть производная пути по времени:
есть производная пути по времени:  , ускорение в момент
, ускорение в момент 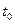 есть
есть  .
.
При движении точки по окружности: угловая скорость вращения  в данный момент равна производной от угла поворота
в данный момент равна производной от угла поворота  по времени:
по времени:  . Угловое ускорение точки есть первая производная от угловой скорости
. Угловое ускорение точки есть первая производная от угловой скорости  или вторая производная от угла поворота по времени
или вторая производная от угла поворота по времени 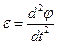 .
.
Сила тока в данный момент времени равна производной от количества протекшего электричества по времени:  .
.
Химическое истолкование производной. Пусть 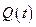 - концентрация вещества, получаемого в ходе химической реакции в момент времени
- концентрация вещества, получаемого в ходе химической реакции в момент времени  . Тогда
. Тогда  - скорость реакции в момент
- скорость реакции в момент 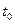 .
.
Пример 1. В точках пересечения эллипсов  ,
, 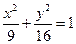 найти угол между ними.
найти угол между ними.
Решение: Эллипсы расположены симметрично относительно координатных осей. Поэтому рассмотрим только первый квадрат координатной плоскости.
Решив систему  найдем точку пересечения эллипсов
найдем точку пересечения эллипсов  . Из уравнения первого эллипса получаем
. Из уравнения первого эллипса получаем  , т.е.
, т.е.  . Следовательно
. Следовательно  . Аналогично, для второго эллипса получим
. Аналогично, для второго эллипса получим  . По формуле
. По формуле  ,
,  получим:
получим:  .
.
Итак, эллипсы пересекаются в четырех точках под углом  , т.е. под углом, равным приблизительно
, т.е. под углом, равным приблизительно 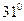 .
.
Пример 2. Высота  снаряда, вылетевшего с начальной скоростью
снаряда, вылетевшего с начальной скоростью  под углом
под углом 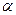 к горизонту, изменяется по закону
к горизонту, изменяется по закону  , где
, где  - время,
- время,  - ускорение силы тяжести. В какой момент скорость изменения высоты снаряда над горизонтом равна нулю?
- ускорение силы тяжести. В какой момент скорость изменения высоты снаряда над горизонтом равна нулю?
Решение: Вычислим производную функции  .
.
Следовательно, скорость изменения высоты снаряда нал горизонтом равна нулю при  .
.
Найти уравнения касательной и нормали к данной кривой в данной точке:
1.  ,
,  .
.
2.  ,
,  . Ответ:
. Ответ:  ,
,  .
.
3.  ,
,  .
.
4. 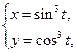
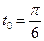 .
.
5. к эллипсу  ,
,  .
.
6.  ,
,  . Ответ:
. Ответ:  .
.
7.  ;
; 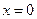 . Ответ:
. Ответ:  .
.
8. 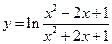 ,
, 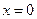 . Ответ:
. Ответ:  .
.
9.  ,
, 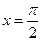 . Ответ:
. Ответ:  .
.
10. 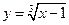 ,
,  . Ответ:
. Ответ:  .
.
11. 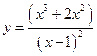 ,
, 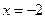 . Ответ:
. Ответ: 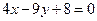 .
.
12.  ,
,  . Ответ:
. Ответ:  .
.
13.  ,
,  . Ответ:
. Ответ:  .
.
14.  Ответ:
Ответ:  .
.
15. 
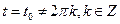 . Ответ:
. Ответ:  .
.
16. Найти углы, под которыми пересекаются линии, заданные уравнениями 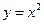 и
и  . Ответ:
. Ответ:  ,
,  .
.
17. Найти угол между кривыми:
a)  и
и  . Ответ:
. Ответ:  .
.
b)  и
и  . Ответ:
. Ответ:  .
.
Найти углы, под которыми график функции  пересекает ось абсцисс:
пересекает ось абсцисс:
18.  . Ответ:
. Ответ:  .
.
19.  . Ответ: В точках
. Ответ: В точках  синусоида
синусоида
пересекает ось абсцисс под углом  .
.
20.  . Ответ: В точках
. Ответ: В точках  угол
угол  ,
,
в точках  угол
угол  .
.
21.  . Ответ:
. Ответ:  .
.
22.  .
.
Ответ: в точке  угол
угол  , в точке
, в точке  угол
угол  .
.
23.  . Ответ:
. Ответ:  .
.
24.  . Ответ:
. Ответ:  .
.
25.  .
.
Ответ: в точках  и
и  угол
угол 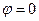 ,
,
в точке  угол
угол  .
.
26.  .
.
Ответ: в точке  угол
угол  ,
,
в точке 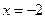 угол
угол  .
.
27.  Ответ:
Ответ:  .
.
28.  Ответ: 0.
Ответ: 0.
29. 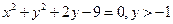 .
.
Ответ: в точке  угол
угол  ,
,
в точке  угол
угол  .
.
Найти точки, в которых касательные к графику функции  параллельны оси абсцисс:
параллельны оси абсцисс:
30.  . Ответ: (-1;14), (2;-13).
. Ответ: (-1;14), (2;-13).
31.  . Ответ: (0;-1), (1;-6), (-2;-33).
. Ответ: (0;-1), (1;-6), (-2;-33).
32.  . Ответ: (-1;-58), (1;54), (7;-2106).
. Ответ: (-1;-58), (1;54), (7;-2106).
33.  . Ответ:
. Ответ:  .
.
34. 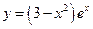 . Ответ:
. Ответ:  .
.
35.  . Ответ:
. Ответ:  .
.
36.  . Ответ:
. Ответ:  .
.
37.  Ответ:
Ответ:  .
.
38.  . Ответ:
. Ответ:  .
.
39. На кривой 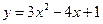 найти точку
найти точку  , в которой касательная параллельна прямой
, в которой касательная параллельна прямой  . Ответ:
. Ответ:  .
.
40. Найти точку линии  , в которой касательная перпендикулярна прямой
, в которой касательная перпендикулярна прямой  , составить уравнение этой касательной. Сделать чертеж. Ответ:
, составить уравнение этой касательной. Сделать чертеж. Ответ:  .
.
41. Точка движется вдоль прямой по закону  . Найти скорость и ускорение точки в момент времени
. Найти скорость и ускорение точки в момент времени 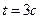 .
.
Ответ: 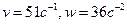 .
.
42. Угол поворота шкива в зависимости от времени задан формулой  . Найти угловую скорость и ускорение при
. Найти угловую скорость и ускорение при  .
.
Ответ: угловая скорость равна  ,
,
а угловое ускорение не зависит от времени и равно  .
.
Определить, в каких точках и под каким углом пересекаются кривые:
43.  ,
,  . Ответ:
. Ответ:  .
.
44. 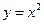 ,
,  . Ответ:
. Ответ:  .
.
45.  ,
,  . Ответ:
. Ответ:  .
.
46.  ,
,  . Ответ:
. Ответ:  .
.
47.  ,
,  . Ответ:
. Ответ:  .
.
48.  ,
,  . Ответ:
. Ответ:  .
.
49.  ,
,  . Ответ:
. Ответ:  .
.
50.  ,
,  . Ответ:
. Ответ:  .
.
51.  и
и  . Ответ:
. Ответ:  .
.
52.  и
и  . Ответ:
. Ответ:  .
.
53. Найти уравнение нормали к эллипсу  в точке
в точке  . Ответ:
. Ответ: 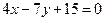 .
.
54. Найти уравнение нормали к гиперболе  в точке
в точке 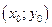 .
.
Ответ:  .
.
Найти угол между касательной и полярным радиусом точки касания для следующих кривых:
55. Спирали Архимеда  . Ответ:
. Ответ:  .
.
56. Гиперболической спирали  . Ответ:
. Ответ:  .
.
57. Логарифмической спирали  . Ответ:
. Ответ:  .
.
58. Кардиоиды  . Ответ:
. Ответ:  .
.
59. Дуги лемнискаты Бернулли  . Ответ:
. Ответ:  .
.
60. Точка движется по параболе  так, что ее абсцисса изменяется по закону
так, что ее абсцисса изменяется по закону  (
(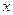 измеряется в метрах,
измеряется в метрах,  - в секундах). Какова скорость изменения ординаты точки через 9 с после начала движения? Ответ:
- в секундах). Какова скорость изменения ординаты точки через 9 с после начала движения? Ответ:  .
.
61. Радиус шара возрастает равномерно со скоростью 5 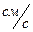 . Какова скорость изменения объема шара в момент, когда его радиус становится равным 50
. Какова скорость изменения объема шара в момент, когда его радиус становится равным 50  ? Ответ: 0,05
? Ответ: 0,05  .
.
62. Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот сделан за 8 с. Найти угловую скорость через 64 с после начала движения. Ответ:  .
.
63. По оси абсцисс движутся две точки, имеющие законы движения: 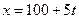 и
и  . С какой скоростью удаляются они друг от друга в момент встречи (
. С какой скоростью удаляются они друг от друга в момент встречи (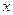 измеряется в метрах,
измеряется в метрах,  - в секундах)? Ответ:
- в секундах)? Ответ:  .
.
64. Паром подтягивается к берегу при помощи каната, который наматывается на ворот со скоростью 3  . Определить скорость движения парома в тот момент, когда он находится в 25 м от берега, если ворот расположен на берегу выше поверхности воды на 4м.
. Определить скорость движения парома в тот момент, когда он находится в 25 м от берега, если ворот расположен на берегу выше поверхности воды на 4м.
Ответ:  .
.
65. Под каким углом пересекаются кривые  и
и  в точке (1;1)? Ответ:
в точке (1;1)? Ответ:  .
.
66. Определить среднюю скорость изменения функции  на отрезке
на отрезке  . Ответ:
. Ответ: 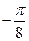 .
.
67. Найти расстояние от полюса до произвольной касательной кривой  . Ответ:
. Ответ:  .
.
68. Записать в декартовых и в полярных координатах уравнение нормали к кардиоиде  в точке с полярным углом
в точке с полярным углом 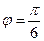 .
.
Ответ:  ,
,  .
.
69. Точка движется по спирали Архимеда  так, что угловая скорость вращения ее полярного радиуса постоянна и равна
так, что угловая скорость вращения ее полярного радиуса постоянна и равна 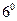 в секунду. Определить скорость удлинения полярного радиуса
в секунду. Определить скорость удлинения полярного радиуса  , если
, если  . Ответ:
. Ответ:  .
.
Правило Лопиталя
Пусть в некоторой окрестности точки  функции
функции 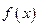 и
и  дифференцируемы и
дифференцируемы и  . Если
. Если  или
или 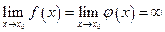 , т.е. частное
, т.е. частное  в точке
в точке  представляет собой неопределенность вида
представляет собой неопределенность вида  или
или  , то
, то
 , если предел в правой части этого равенства существует.
, если предел в правой части этого равенства существует.
Другими словами: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует. Аналогичное утверждение справедливо и в случае, если  .
.
Если частное  в точке
в точке  также есть неопределенность вида
также есть неопределенность вида  или
или  и производные
и производные  и
и  удовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т.д.
удовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т.д.
В случае неопределенности вида 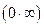 или
или  следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности вида
следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности вида  или
или  и далее воспользоваться правилом Лопиталя.
и далее воспользоваться правилом Лопиталя.
В случае неопределенности вида  или
или  , или
, или  следует прологарифмировать данную функцию и найти предел ее логарифма.
следует прологарифмировать данную функцию и найти предел ее логарифма.
Замечание: В правой части формулы Лопиталя берется отношение производных, а не производная отношения.
Пример 1. Найти  .
.
Решение: Имеем неопределенность вида  . Применяя правило Лопиталя, получим:
. Применяя правило Лопиталя, получим:  .
.
Пример 2. Найти  .
.
Решение:  .
.
Неопределенность вида  по-прежнему сохраняется. Применим правило Лопиталя еще раз.
по-прежнему сохраняется. Применим правило Лопиталя еще раз.
 .
.
Пример 3. Найти  .
.
Решение: Имеем неопределенность вида 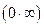 . Переписывая выражение в виде
. Переписывая выражение в виде  , получим неопределенность вида
, получим неопределенность вида  . Применяя правило Лопиталя, получим
. Применяя правило Лопиталя, получим  .
.
Замечание: Если имеется неопределенность вида  или
или  при вычислении предела функции
при вычислении предела функции 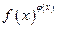 , то логарифм этой функции представляет собой неопределенность вида
, то логарифм этой функции представляет собой неопределенность вида 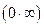 . При этом
. При этом  .
.
Пример 4. Найти  .
.
Решение: 
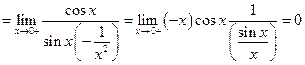 , т.к.
, т.к. 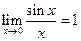 .
.
Отсюда  .
.
Правило Лопиталя является эффективным методом раскрытия неопределенностей. Однако применение его не всегда приводит к цели.
Пример 5. Найти  .
.
Решение: Если применить правило Лопиталя, то получим
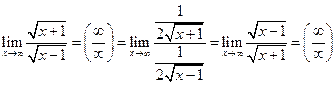 ,
,
т.е. числитель и знаменатель просто меняются местами. Неопределенность же сохраняется. Если применить правило Лопиталя вторично, то функция под знаком предела примет первоначальный вид. Таким образом, использование правила Лопиталя в данном случае не позволит раскрыть неопределенность. В то же время легко установить, что  .
.
Пример 6. Найти  .
.
Решение: Если применить правило Лопиталя, т.е.
 ,
,
то можно сделать ошибочный вывод о том, что предел данной функции не существует, т.к. не существует  . На самом деле
. На самом деле  , т.к.
, т.к.  (произведение бесконечно малой функции на ограниченную функцию).
(произведение бесконечно малой функции на ограниченную функцию).
Пример 7. Найти  .
.
Решение: Если  , то имеем неопределенность
, то имеем неопределенность  . Прологарифмируем данную функцию
. Прологарифмируем данную функцию 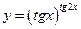 .
.
Получим: 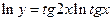 .
.
Далее: 
 .
.
Следовательно,  или
или  .
.
Найти пределы следующих функций:
Неопределенность вида  .
.
1. 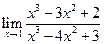 . Ответ:
. Ответ: 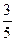 .
.
2.  . Ответ:
. Ответ:  .
.
3.  . Ответ:
. Ответ:  .
.
4.  . Ответ: 18.
. Ответ: 18.
5.  . Ответ:
. Ответ:  .
.
6.  . Ответ: 0,18.
. Ответ: 0,18.
Неопределенность вида  .
.
1.  . Ответ: 1.
. Ответ: 1.
2.  ,
,  . Ответ: 0.
. Ответ: 0.
3.  . Ответ:
. Ответ: 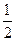 .
.
4. 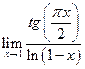 . Ответ:
. Ответ:  .
.
5.  . Ответ: 0.
. Ответ: 0.
Неопределенность вида 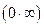 .
.
1.  . Ответ:
. Ответ:  .
.
2.  . Ответ: 1.
. Ответ: 1.
3.  Ответ: 0.
Ответ: 0.
Неопределенность вида  .
.
1.  . Ответ:
. Ответ:  .
.
2.  . Ответ:
. Ответ: 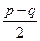 .
.
3.  . Ответ:
. Ответ:  .
.
Неопределенности вида  ,
,  ,
,  .
.
1.  . Ответ: 1.
. Ответ: 1.
2.  . Ответ:
. Ответ: 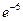 .
.
3.  . Ответ: 2.
. Ответ: 2.
4.  . Ответ:
. Ответ:  .
.
Самостоятельная работа
Найти пределы:
1.  . Ответ:
. Ответ:  .
.
2.  . Ответ:
. Ответ:  .
.
3.  . Ответ:
. Ответ:  .
.
4.  . Ответ:
. Ответ: 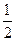 .
.
5.  . Ответ:
. Ответ:  .
.
6.  . Ответ: 1.
. Ответ: 1.
7. 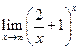 . Ответ:
. Ответ:  .
.
8.  . Ответ:
. Ответ:  .
.
9.  . Ответ:
. Ответ:  .
.
10.  . Ответ:
. Ответ:  .
.
11.  . Ответ: 1.
. Ответ: 1.
12.  . Ответ: 3.
. Ответ: 3.
13. 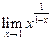 . Ответ:
. Ответ:  .
.
14.  .
.
15.  .
.
16. 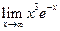 .
.
17.  .
.
18. 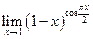 .
.
19.  .
.
20.  .
.
Примерный вариант контрольной работы
1. Найти 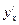 :
:
a)  , b)
, b)  , c)
, c)  ,
,
d)  e)
e)  .
.
2. Найти  : a)
: a) 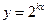 , b)
, b) 
3. Составить уравнения касательных и нормалей в указанных точках к следующим кривым:
a)  ,
,  , b)
, b) 
 .
.
4. Вычислить приближенно с помощью дифференциала значение функции  при заданном значении
при заданном значении  :
: 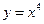 ,
,  .
.
5. Вычислить  с помощью правила Лопиталя.
с помощью правила Лопиталя.






