Производной n-го порядка называется производная от производной (n-1)-го порядка.
Пример 1. Найти производные до n-го порядка включительно от функции  .
.
Решение:  ,
, 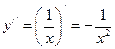 ,
,  ,
,  и т. д.
и т. д.
Очевидно, что производная n-го порядка  .
.
Вторая производная от неявной функции  находится дифференцированием функции
находится дифференцированием функции  по переменной
по переменной 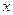 , учитывая при этом, что
, учитывая при этом, что  есть функция от
есть функция от 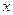 .
.
Пример 2. Найти  для неявной функции
для неявной функции  .
.
Решение:
Дифференцируем правую и левую часть по 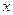 :
:  .
.
Разрешая относительно производной, получим:  .
.
Дифференцируем еще один раз по 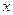 :
:  .
.
Подставляя в последнее выражение значение  , получим
, получим

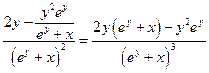 .
.
Вторая производная от функции  по
по 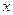 , заданной параметрически, равна
, заданной параметрически, равна 
 .
.
Третья производная  и т.д.
и т.д.
Пример 3. Найти 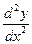 для функции
для функции  .
.
Решение: Найдем первую производную:  .
.
Вторую производную находим по формуле:
 .
.
Производная n-го порядка от произведения двух функций удобнее находить по формуле Лейбница.

 ,где
,где  - биномиальные коэффициенты,
- биномиальные коэффициенты,  ,
, 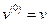 .
.
Пример 4. Найти 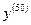 для функции
для функции  .
.
Решение: Положим  ,
,  . Тогда
. Тогда  ,
,  ,
,  ,
,  . По формуле Лейбница все слагаемые, кроме трех последних, равны нулю, поэтому получаем:
. По формуле Лейбница все слагаемые, кроме трех последних, равны нулю, поэтому получаем:

 .
.
Для данных функций найти производные указанного порядка:
1.  ,
,  -?
-?
2.  ,
,  -?
-?
3.  ,
,  -?
-?
4.  ,
,  -?
-?
5.  ,
,  -?
-?
6.  ,
,  -?
-?
7. 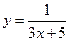 ,
,  -?
-?
8. 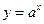 ,
,  -? Ответ:
-? Ответ:  ,
, 
9.  ,
,  -? Ответ:
-? Ответ: 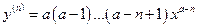 .
.
Если 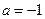 , то
, то  . Если
. Если  , то
, то  .
.
10.  ,
,  -? Ответ:
-? Ответ:  .
.
11.  ,
,  -? Ответ:
-? Ответ:  .
.
12.  ,
,  -? Ответ:
-? Ответ: 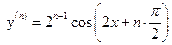 .
.
13.  ,
,  -? Ответ:
-? Ответ: 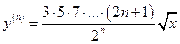 .
.
14.  ,
,  -? Ответ:
-? Ответ: 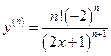 .
.
15. 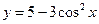 ?
?  -? Ответ:
-? Ответ:  .
.
16.  ,
,  -? Ответ:
-? Ответ:  .
.
17.  ,
,  -? Ответ:
-? Ответ:  .
.
18. 
 -? Ответ:
-? Ответ:  .
.
19. 
 -? Ответ:
-? Ответ:  .
.
20. 
 -? Ответ:
-? Ответ:  .
.
21. 
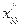 -? Ответ:
-? Ответ:  .
.
22. 
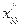 -? Ответ:
-? Ответ:  .
.
23. 
 -? Ответ:
-? Ответ:  .
.
24. 
 -? Ответ:
-? Ответ:  .
.
25.  ,
,  -? Ответ:
-? Ответ:  .
.
26.  ,
,  -?
-?
Ответ:  .
.
27.  ,
,  -? Ответ:
-? Ответ:

28.  ,
,  -? Ответ:
-? Ответ:  .
.
29.  ,
,  -?
-?
Ответ:  .
.
30.  ,
,  -?
-?
Ответ: 
 .
.
31.  ,
,  -? Ответ:
-? Ответ:  .
.
32.  ,
,  -? Ответ:
-? Ответ:  .
.
33.  ,
,  -? Ответ:
-? Ответ:  .
.
34.  ,
,  -?
-?
Ответ:  , где
, где 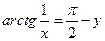 .
.
35.  ,
,  -? Ответ:
-? Ответ:  .
.
36.  ,
,  -? Ответ:
-? Ответ:  .
.
37.  ,
, 
 -? Ответ:
-? Ответ:  .
.
38.  ,
,  -?
-?
Ответ: 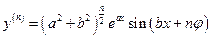 , где
, где  ,
, 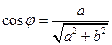 .
.
39.  ,
,  -?
-?
Указание: Преобразовать выражение к виду:  .
.
По формуле п. 36
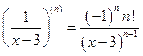 и
и  .
.
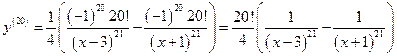 .
.
40.  ,
,  -? Ответ:
-? Ответ:  .
.
Указание: в формуле п. 38 положить  .
.
42.  ,
,  -? Ответ:
-? Ответ:  .
.
Указание: в формуле п. 38 положить  .
.
41. 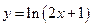 ,
,  -? Ответ:
-? Ответ:  .
.
Указание: Находим первую производную  .
.
По формуле п. 36
 .
.
43.  ,
,  -?
-?
Указание: Записать функцию в виде  и, применяя формулу Лейбница, продифференцировать n раз. При
и, применяя формулу Лейбница, продифференцировать n раз. При  будем иметь
будем иметь  . Откуда при
. Откуда при 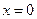 получим
получим  или
или  . Полученная рекуррентная формула позволяет определить
. Полученная рекуррентная формула позволяет определить  - ую производную в точке
- ую производную в точке 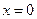
 . Значения
. Значения  находятся непосредственно
находятся непосредственно
 ,
,  .
.
 ,
,
 .
.
44.  ,
,  -? Ответ:
-? Ответ:  .
.
45.  .
.
Дифференциал функции
Дифференциал (первого порядка) функции  -это главная часть ее приращения, линейная относительно приращения аргумента. Дифференциал аргумента равен его приращению:
-это главная часть ее приращения, линейная относительно приращения аргумента. Дифференциал аргумента равен его приращению:  . Дифференциал функции равен произведению ее производной на дифференциал аргумента
. Дифференциал функции равен произведению ее производной на дифференциал аргумента  .
.
Основные свойства дифференциала:
1.  , где
, где 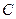 - const.
- const.
2.  .
.
3.  .
.
4.  .
.
5.  ,
,  .
.
6.  ,
,  . Форма дифференциала первого порядка не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. В этом состоит свойство инвариантности формы дифференциала первого порядка.
. Форма дифференциала первого порядка не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. В этом состоит свойство инвариантности формы дифференциала первого порядка.
Дифференциалом второго порядка функции  называется дифференциал от дифференциала первого порядка:
называется дифференциал от дифференциала первого порядка:  .
.
Аналогично определяется дифференциал третьего порядка:  . Дифференциал n-го порядка:
. Дифференциал n-го порядка:  .
.
Если  и
и 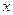 - независимая переменная, то дифференциалы высших порядков вычисляются по формулам:
- независимая переменная, то дифференциалы высших порядков вычисляются по формулам:
 ,
,  ,…..,
,…..,  .
.
Если  ,
,  , то
, то  , где дифференцирование функции
, где дифференцирование функции  выполняется по переменной
выполняется по переменной  . Это имеет место и для дифференциалов более высоких порядков.
. Это имеет место и для дифференциалов более высоких порядков.
 .
.
Дифференциалы второго и более высоких порядков не обладают свойством инвариантности формы.
Геометрически дифференциал представляет собой приращение ординаты касательной к графику функции в точке 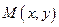 .
.
Если приращение аргумента мало по абсолютной величине, то  и
и  . Таким образом, дифференциал функции может применяться для приближенных вычислений.
. Таким образом, дифференциал функции может применяться для приближенных вычислений.
Абсолютная величина разности между истинным значением какой-либо величины  и ее приближенным значением
и ее приближенным значением  называется абсолютной погрешностью и обозначается
называется абсолютной погрешностью и обозначается  .
.
Абсолютная величина отношения абсолютной погрешности к истинному значению называется относительной погрешностью и обозначается  . Относительная погрешность обычно выражается в процентах
. Относительная погрешность обычно выражается в процентах 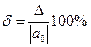 .
.
Если приращение функции заменить ее дифференциалом, то получим приближенное значение приращения  . В этом случае абсолютная погрешность равна
. В этом случае абсолютная погрешность равна  , а относительная погрешность будет
, а относительная погрешность будет 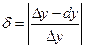 .
.
С помощью дифференциала функции вычисляют абсолютную погрешность функции  , если известна абсолютная погрешность
, если известна абсолютная погрешность 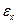 аргумента. В практических задачах значения аргумента находятся с помощью измерений, и его абсолютная погрешность считается известной.
аргумента. В практических задачах значения аргумента находятся с помощью измерений, и его абсолютная погрешность считается известной.
Пусть требуется вычислить значение функции  при некотором значении аргумента
при некотором значении аргумента 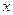 , истинная величина которого нам известна, но дано его приближенное значение
, истинная величина которого нам известна, но дано его приближенное значение  с абсолютной погрешностью
с абсолютной погрешностью 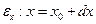 ,
,  . Тогда
. Тогда
 .
.
Отсюда видно, что  .
.
Относительная погрешность функции  выражается формулой
выражается формулой
 .
.
Пример 1. Найти дифференциал функции  .
.
Решение:  .
.
Пример 2. Найти все дифференциалы функции  .
.
Решение:  ,
,
 ,
,  ,
,
 ,
,  .
.
Пример 3. Найти  для неявно заданной функции
для неявно заданной функции  .
.
Решение: Функция задана неявно. Находим первую производную
 , тогда
, тогда  .
.
Вычислим вторую производную
 , отсюда
, отсюда  .
.
Пример 4. Выразить дифференциал сложной функции через независимую переменную и дифференциал:  ,
,  ,
,  .
.
Решение:  .
.  .
.
Пример 5. Вычислить приближенное значение  .
.
Решение: Рассмотрим функцию  . Полагая
. Полагая  ,
,  и применяя формулу
и применяя формулу  , получим:
, получим:
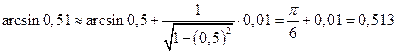 .
.
Пример 6. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м.
Решение: Воспользуемся формулой  . Полагая
. Полагая 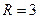 ,
,  , имеем
, имеем  . Следовательно, приближенное значение площади круга составляет
. Следовательно, приближенное значение площади круга составляет  .
.
Пример 7. Для функции  найти приращение ординаты касательной и приращение функции при переходе аргумента
найти приращение ординаты касательной и приращение функции при переходе аргумента 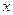 от значения
от значения  к
к  .
.
Решение: согласно геометрическому смыслу дифференциала, приращению ординаты касательной соответствует дифференциал функции 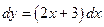 .
.
При  и
и  получим
получим  .
.
Приращение функции находим по формуле
 .
.
Следовательно, приращение ординаты касательной равно 0,7, а приращение функции 0,71. Т. к. 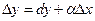 , то
, то  .
.
Пример 8. Найти дифференциал и приращение функции  в точке
в точке  и
и 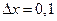 . Найти абсолютную и относительную погрешности значения функции при замене приращения функции ее дифференциалом.
. Найти абсолютную и относительную погрешности значения функции при замене приращения функции ее дифференциалом.
Решение: Имеем:  ,
,
 .
.
При  и
и 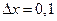 получим:
получим:
 ,
,  .
.
Абсолютная погрешность  , а относительная погрешность
, а относительная погрешность  .
.
Пример 9. При измерении сторона куба 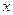 оказалась равной 4 см. При этом максимально возможная погрешность измерения
оказалась равной 4 см. При этом максимально возможная погрешность измерения  находится в пределах
находится в пределах 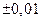 см. Определить абсолютную и относительную погрешности при вычислении объема куба.
см. Определить абсолютную и относительную погрешности при вычислении объема куба.
Решение: Объем куба равен  см
см  .
.
Возможная неточность измерения  .
.
Отсюда абсолютная погрешность  .
.
Относительная погрешность 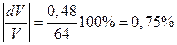 .
.
Пример 10. Найти приближенно  .
.
Решение: Полагаем  , тогда
, тогда  ,
,
 .
.
Если принять  , то
, то  ,
,  .
.
Найти дифференциалы указанных порядков от функций:
1. 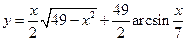 ,
,  -?. Ответ:
-?. Ответ:  .
.
2.  ,
,  -? Ответ:
-? Ответ:  .
.
3.  ,
,  -? Ответ:
-? Ответ:  .
.
4.  ,
,  -? Ответ:
-? Ответ: 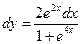 .
.
5.  ,
,  ,
,  ,
,  -? Ответ:
-? Ответ:  .
.
 ,
,  .
.
6.  ,
,  -?
-?
Ответ:  .
.
7.  ,
,  -? Ответ:
-? Ответ:  .
.
8.  ,
,  -? Ответ:
-? Ответ:  .
.
9. 
 -? Ответ:
-? Ответ:  .
.
10. 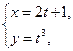
 -? Ответ:
-? Ответ:  .
.
11.  ,
,  -? Ответ:
-? Ответ:  .
.
12.  ,
,  -? Ответ:
-? Ответ:  .
.
13. 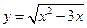 ,
,  .
.  -? Ответ:
-? Ответ:  ,
,  .
.
14.  ,
,  ,
,  -?
-?
Ответ:  ,
,  .
.
15. 
 -?
-?
Найти приближенное значение:
16.  . Ответ: 0,811.
. Ответ: 0,811.
17. 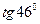 . Ответ: 1,035.
. Ответ: 1,035.
18.  . Ответ: 0,078.
. Ответ: 0,078.
19.  . Ответ: 1,9938.
. Ответ: 1,9938.
20.  . Ответ: 2,02.
. Ответ: 2,02.
21. 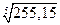 . Ответ:3,03.
. Ответ:3,03.
22.  . Ответ:
. Ответ:  .
.
23.  . Ответ:
. Ответ:  .
.
24.  . Ответ: 0,1.
. Ответ: 0,1.
25.  . Ответ:
. Ответ:  .
.
26. Определить, на сколько приблизительно увеличится объем шара, если его радиус  см увеличить на 0,2см. Ответ: 565
см увеличить на 0,2см. Ответ: 565  .
.
27. Вычислить приближенное значение площади круга, радиус которого равен 3,02 м. Ответ:  .
.
28. Сравнить приращение и дифференциал функции  .
.
Ответ:  ,
,  .
.
29. Вычислить  ,
,  для функции
для функции 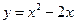 при
при  и
и  .
.
Ответ:  ,
,  .
.
30. Найти приближенное значение объема шара радиуса 2,01 м.
Ответ:  .
.
31. Найти приближенное значение 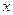 из уравнения:
из уравнения:
 . Ответ:
. Ответ:  .
.
32. Найти приближенно значение объема шара радиуса  .
.
Ответ:  .
.
33. Ребра куба увеличены на 1см. При этом дифференциал  объема
объема  куба оказался равным 12 см
куба оказался равным 12 см  . Найти первоначальную длину ребер. Ответ: 2 см.
. Найти первоначальную длину ребер. Ответ: 2 см.
34. Радиус круга увеличен на 1см. Дифференциал площади круга оказался при этом равным 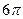 см
см  . Найти первоначальную величину радиуса. Ответ: 3 см.
. Найти первоначальную величину радиуса. Ответ: 3 см.
35. Определить приблизительно относительную погрешность при вычислении поверхности сферы, если при определении ее радиуса относительная погрешность составила  . Ответ:
. Ответ:  .
.






