При решении задач на максимум и минимум по условиям задачи следует:
1. Составить функцию, приняв одну из переменных в качестве независимой. Интервал изменения независимой переменной определяется условиями задачи.
2. Выразить все остальные переменные, входящие в составленную функцию, через выбранную независимую переменную.
3. Получить аналитическое выражение функции через выбранную независимую переменную.
3. Исследовать эту функцию на экстремум в критических точках, принадлежащих области изменения независимой переменной.
4. Найти наибольшее и наименьшее значения полученной функции из значений на границах области изменения независимой переменной и в точках экстремума.
Пример 1: Объем цилиндра 
. Найти радиус основания, при котором цилиндр имеет наименьшую полную поверхность.
Решение: Полную поверхность цилиндра принимаем за функцию.
,
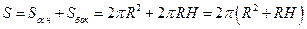где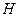 
- высота цилиндра, 
- радиус основания. Объем цилиндра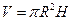 
. Отсюда 
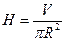. Исключая 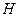из выражения полной поверхности цилиндра, получим 
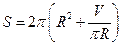. Вычисляя производную по , получим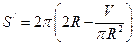 
. Приравнивая к нулю 
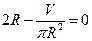, находим, что минимум наименьшей полной поверхности будет при радиусе 
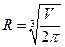. Действительно, вторая производная при 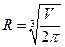равна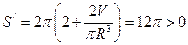 
. То есть найденное значение радиуса определяет наименьшую полную поверхность.
1. Число 64 разложить на два таких множителя, чтобы сумма их квадратов была наименьшей. Ответ: 8;8.
2. Из углов квадратного листа железа со стороной 
нужно вырезать одинаковые квадраты так, чтобы, согнув лист, получить коробку наибольшей вместимости. Какова должна быть сторона квадрата?
Ответ: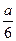 
.
3. Среди всех равнобедренных треугольников, вписанных в данный круг, найти треугольник с наибольшим периметром.
Ответ: Равносторонний треугольник.
4. Определить размеры закрытой коробки объема с квадратным основанием, на изготовление которой расходуется наименьшее количество материала. Ответ: Высота коробки должна быть равна стороне основания, т.е. должна быть кубом с ребром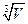 
.
5. Найти радиус основания цилиндра наибольшего объема, вписанного в шар радиуса . Ответ: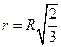 
.
Указания: Пусть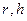 
- соответственно радиус основания и высота цилиндра, вписанного в шар радиуса , 
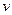- объем цилиндра. Тогда 
.
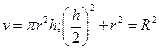6. Бак цилиндрической формы без крышки должен вмещать литров воды. Каковы должны быть его размеры, чтобы на его изготовление потребовалось наименьшее количество железа?
Ответ: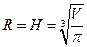 
.
7. Одна сторона прямоугольного участка земли площадью 800 
примыкает к реке, остальные огораживаются забором. Каковы должны быть размеры участка, чтобы длина забора была наименьшей?
Ответ: 40 м, 20 м.
8. Какой из конусов, вписанных в шар радиуса , имеет наибольший объем? Ответ: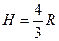 
.
9. Найти стороны прямоугольника наибольшей площади, вписанного в эллипс 
. Ответ: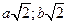 
.
