Алтайский государственный технический университет им. И.И. Ползунова
СБОРНИК ЗАДАНИЙ
ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
КУРС
СЕМЕСТР
Часть
Дифференциальное исчисление
Функций одного переменного
Г. БАРНАУЛ
Год
Составитель: Исаева М.В.
Данный сборник заданий для практических занятий по математике является составной частью комплекса сборников, направленных на активизацию работы студентов по изучению программы курса.
В сборник включены: программа второго семестра дисциплины ЕН.Ф.01 «МАТЕМАТИКА», список рекомендуемой литературы, основные положения учебного материала, дополненные задачами с решениями, наборы заданий различной степени сложности по дифференциальному исчислению функции одного переменного
Краткие теоретические сведения, снабженные большим количеством примеров с иллюстрацией методов их решения, позволяют использовать сборник для различных видов обучения, в том числе для самостоятельной работы студентов и для аудиторных занятий.
Для студентов групп СТФ.
ОГЛАВЛЕНИЕ
Дифференциальное исчисление функции одного переменного ……………..………………………………………..……….3
1. Непосредственное дифференцирование…………….......................…….3
- Правила дифференцирования….……..……………………………….3
- Таблица производных элементарных функций……………………....4
2. Специальные приемы дифференцирования……………..........…….............10
2.1. Логарифмическое дифференцирование……………………....…..10
2.2. Дифференцирование функций, заданных неявно………………..10
2.3. Дифференцирование функций, заданных параметрически……..11
3. Производные высших порядков….......................................................... 12
4. Дифференциал функции ……………………..………………................17
5. Геометрический и физический смысл производной.………..………...22
6. Правило Лопиталя…………………………………….………………....29
7. Примерный вариант контрольной работы …………….………………35
8. Возрастание и убывание функций……………………………….……..35
9. Максимум и минимум функции………………………………………. 38
10. Наибольшее и наименьшее значение функции………………………42
11. Решение задач на максимум и минимум……………………………..44
12. Направление выпуклости кривой. Точки перегиба………………….46
13. Асимптоты кривой……………………………………………………..49
14. Исследование функции и построение графиков……………………..53
15. Варианты типового расчета…………..……………..............................57
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО
Непосредственное дифференцирование
Производной от функции 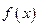 в точке
в точке  называется предел отношения приращения функции к приращению аргумента
называется предел отношения приращения функции к приращению аргумента
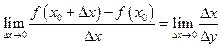 .
.
Если этот предел конечный, то функция называется дифференцируемой в точке  .
.
Процесс нахождения производной называется дифференцированием функции.
Числа 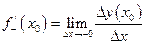 и
и 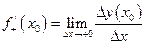 называются соответственно левой и правой производными функции
называются соответственно левой и правой производными функции  в точке
в точке  . Для существования производной функции
. Для существования производной функции  в точке
в точке  необходимо и достаточно, чтобы ее левая и правая производная в этой точке существовали и были равны между собой:
необходимо и достаточно, чтобы ее левая и правая производная в этой точке существовали и были равны между собой: 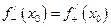 .
.
Правила дифференцирования
1) 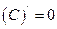 ;
;
2) 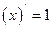 ;
;
3) 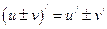 ;
;
4) 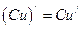 ;
;
5) 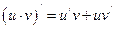 ;
;
6) 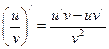 ,
,  ;
;
7) 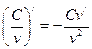 ,
,  ;
;
8) если  ,
, 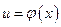 , т.е.
, т.е. 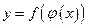 - сложная функция, составленная из дифференцируемых функций, то
- сложная функция, составленная из дифференцируемых функций, то

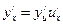 или
или 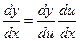 ;
;
9) если для функции  существует обратная дифференцируемая функция
существует обратная дифференцируемая функция 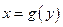 и
и 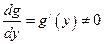 , то
, то 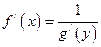 .
.
Таблица производных элементарных функций
1) 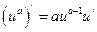 ,
, 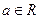 ,
, 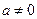 . В частности:
. В частности: 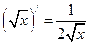 ;
; 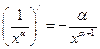 ;
;
2) 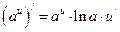 ,
,  ; 3)
; 3) 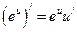 ;
;
4) 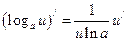 ,
, 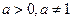 ; 5)
; 5) 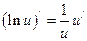
6) 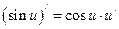 ; 7)
; 7) 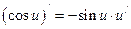 ;
;
8) 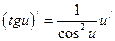 ; 9)
; 9) 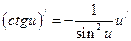 ;
;
10) 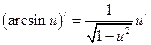 ; 11)
; 11) 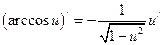 ;
;
12) 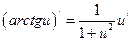 ; 13)
; 13) 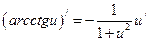 ;
;
14) 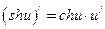 ,
, 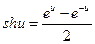 ; 15)
; 15) 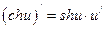 ,
, 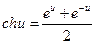 ;
;
16) 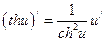 ,
, 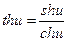 ; 17)
; 17) 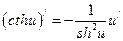 ,
, 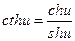 .
.
Пример 1. Пользуясь только определением производной, найти  :
:
a) 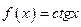 .
.
Имеем: 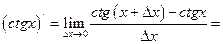
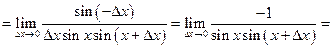
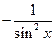 .
.
b) 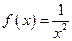 ;
;
c) 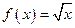 ;
;
d) 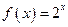 ;
;
e) 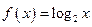 ;
;
f) 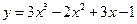 ;
;
g) 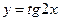 ;
;
h) 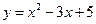 .
.
Пример 2. Для заданной функции 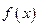 найти
найти 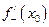 и
и 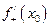 :
:
a)  ,
, 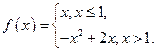
Имеем 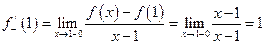 и
и
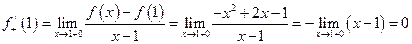 .
.
b) 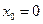 ,
, 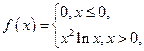
c) 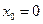 ,
, 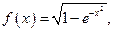
d) 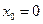 ,
, 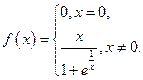
Пример 3. Найти производные 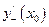 ,
, 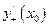 для функций:
для функций:
а) 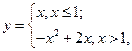
 .
.
Находим производную 
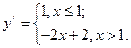
Вычислим пределы производной слева и справа в точке  :
:
 ,
, 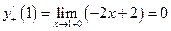 .
.
b) 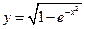 ,
, 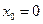 ;
;
c) 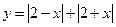 ,
, 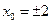 .
.
Пример 4. Найти производные функций:
а) 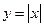 ,
, 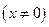 .
.
Представим функцию в виде
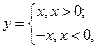 тогда
тогда 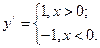
Функция 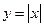 не имеет производной в точке
не имеет производной в точке 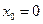 ,
,
так как 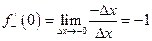 , а
, а 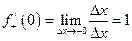 .
.
b) 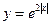 ;
;
c) 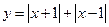 ;
;
d) 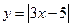 ;
;
e) 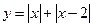 .
.
Пример 5. Найти производные:
а) 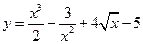 .
.
Преобразуем функцию к виду, удобному для дифференцирования. Пользуясь основными правилами дифференцирования и таблицей производных, имеем
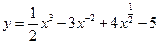 ,
, 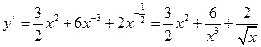 .
.
b) 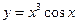 .
.
По формуле производной произведения двух функций:
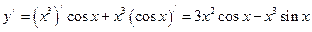 .
.
с) 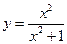 .
.
По формуле производной частного двух функций:
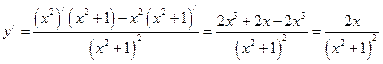 .
.
d) 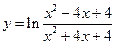 .
.
Упростим логарифмируемое выражение:
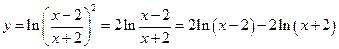 .
.
По правилам дифференцирования имеем:
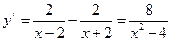 .
.
e) Найти производную функции 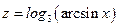 .
.
Правило дифференцирования сложной функции: (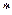 )
) 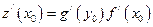 .
.
Полагая 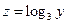 и
и  , имеем
, имеем 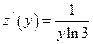 и
и  . Отсюда, согласно (
. Отсюда, согласно (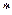 ), получаем
), получаем 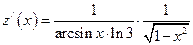 .
.
f) 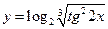 .
.
Упростим логарифмическое выражение:
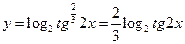 .
.
Дифференцируем как сложную функцию:
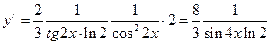
f) 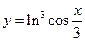 .
.
Дифференцируем как сложную функцию:
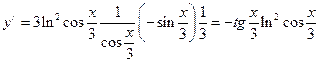 .
.
Пример 6. Найти производные гиперболических и обратных к ним функций:
a) 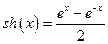 (гиперболический синус),
(гиперболический синус),
b) 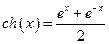 (гиперболический косинус),
(гиперболический косинус),
c) 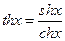 (гиперболический тангенс),
(гиперболический тангенс),
d) 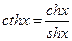 (гиперболический котангенс).
(гиперболический котангенс).
Свойства:
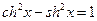 ;
; 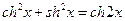 ;
; 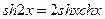 ;
; 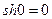 ;
; 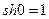 .
.
e) 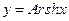 .
.
По правилу дифференцирования обратной функции получим: 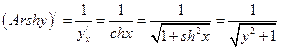 .
.
Переходя к обычным обозначениям, имеем: 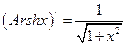 .
.
f) 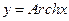 .
.
По правилу дифференцирования обратной функции получим:
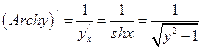 .
.
Переходя к обычным обозначениям, имеем:
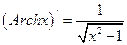 ,
, 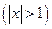 .
.
g) 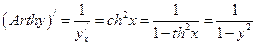 .
. 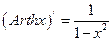 ;
; 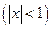 .
.
h) 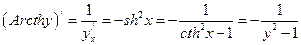 ;
; 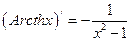 ,
, 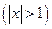 .
.
i) 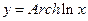 . По правилу дифференцирования сложных функций имеем:
. По правилу дифференцирования сложных функций имеем: 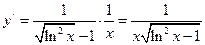 .
.
j) 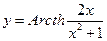 . По правилу дифференцирования сложных функций имеем:
. По правилу дифференцирования сложных функций имеем: 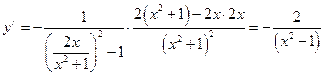 .
.
Пример 7. Найти производные функций:
a) 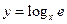 .
.
Если основание логарифма 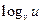 является некоторой функцией
является некоторой функцией 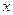 , то при нахождении производной целесообразно перейти к натуральным логарифмам
, то при нахождении производной целесообразно перейти к натуральным логарифмам
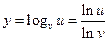 ,
, 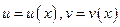 .
.
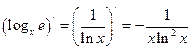 .
.
b) 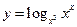 .
.
Перейдем к натуральному логарифму 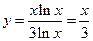 .
.
Отсюда  .
. 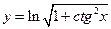 ;
;
c) 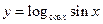 .
.
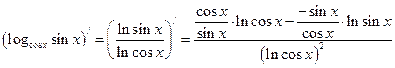
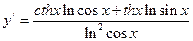 .
.
Найти производные следующих функций:
1. 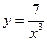 .
.  2.
2. 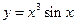 .
.
3. 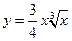 . 4.
. 4. 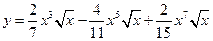 .
.
5. 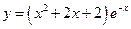 . 6.
. 6. 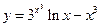 .
.
7. 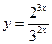 . 8.
. 8. 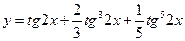 .
.
9. 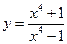 . 10.
. 10. 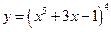 .
.
11. 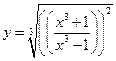 . 12.
. 12. 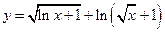 .
.
13. 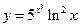 . 14.
. 14. 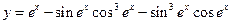 .
.
15. 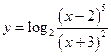 , перед дифференцированием лучше упростить выражение с помощью свойств логарифмов:
, перед дифференцированием лучше упростить выражение с помощью свойств логарифмов: 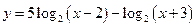 .
.
16. 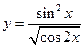 . 17.
. 17. 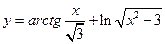 ;
;
18. 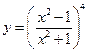 . 19.
. 19. 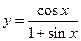 .
.
20. 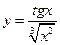 . 21.
. 21. 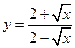 .
.
22. 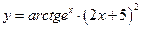 . 23.
. 23. 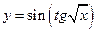 .
.
24. 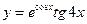 . 25.
. 25. 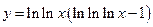 .
.
26. 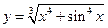 . 27.
. 27. 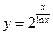 .
.
28. 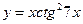 . 29.
. 29. 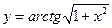 .
.
30. 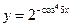 . 31.
. 31. 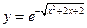 .
.
32. 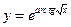 . 33.
. 33. 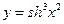 .
.
34. 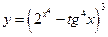 . 35.
. 35. 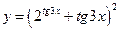 .
.
36. 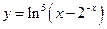 . 37.
. 37. 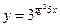 .
.
38. 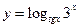 . 39.
. 39. 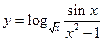 .
.
Найти производные функций и вычислить их значения в точке  :
:
1. 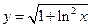 ,
,  . 2.
. 2. 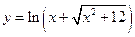 ,
, 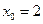 .
.
3. 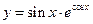 ,
, 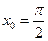 . 3.
. 3. 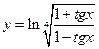 ,
, 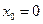 .
.
Самостоятельная работа
Продифференцировать данные функции:
1. 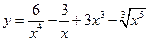 . 2.
. 2. 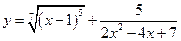 .
.
3.  . 4.
. 4. 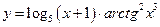 .
.
5. 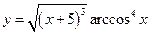 . 6.
. 6. 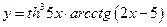 .
.
7. 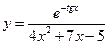 . 8.
. 8. 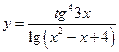 .
.
9.  . 10.
. 10. 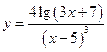 .
.
11. 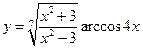 . 12.
. 12. 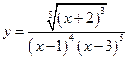 .
.
13. 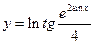 . 14.
. 14. 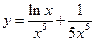 .
.
15. 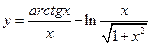 . 16.
. 16. 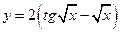 .
.
17. 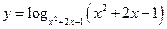 . 18.
. 18. 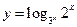 .
.
19. 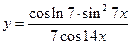 . 20.
. 20. 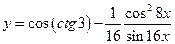 .
.
21.  . 22.
. 22. 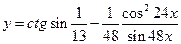 .
.
23. 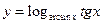 . 24.
. 24. 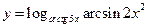 .
.
Специальные приемы дифференцирования






