Так как система сходящихся сил эквивалентна одной равнодействующей, то тело под действием такой системы сил будет находиться в равновесии тогда, когда равнодействующая равна нулю, т. е. силовой многоугольник должен быть замкнут. Условия равновесия в векторной и аналитической форме имеют соответственно следующий вид: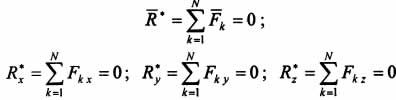 
. Данные равенства содержат заданные и неизвестные величины. Их называют уравнения равновесия.
Алгебраический и векторный моменты силы относительно точки.
Момент силы относительно точки - называется вектор приложенный в этой точке и равный векторному произведению.
М0(F) = r*F
M0(F) перпендикулярен (r,F)
| M0(F) | = r*Fsin(r,F) = F*h (h - плечо силы) (Плечо силы - кратчайшее расстояние (по перпендикуляру) между моментом точки и линией действия силы)
L0 - главный момент системы сил относительно точки О.
Частный случай: если действует система сходящихся сил, то L0 = $M0(F)
Доказательство: L0 = $M0(F) = $(rк * Fк) = r * $Fк = r * (R*) = M0(R*)
M0(R*) = $M0(Fк)
( Другой ответ - немного странноват, но более подробный что ли)
Дополнение:
Теорема Вариньона - момент равнодействующий относительно какой-либо точки равен сумме моментов сил ее составляющих.
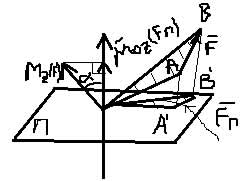
Момент силы относительно оси.
Момент силы относительно оси - проекция на эту ось момента силы относительно любой точки лежащей на оси.
| M0(F) | = 2*SΔOAB
(M0o(F))z = 2*SΔOA'B'
S?OA'B' = SΔOAB*cosα
M0(F) = ±F*h - скалярный момент силы относительно оси.
Знак скалярного момента определяется так, если на встречу вектора момента поворот тела вокруг О против часовой стрелки, то момент положительный.
Момент силы относительно оси не зависит от выбора точки на оси.
(M0'(F))z = (M0(F))z
Второе правило определения момента силы относительно оси: Момент силы относительно оси называется произведение проекции силы на плоскость перпендикулярную оси на плечо этой проекции относительно точки пересечения плоскости с осью.
Момент силы относительно оси Z: M0z(F) = ±hп * Fп
Частные случаи: момент силы относительно оси = 0.
а) Fп = 0
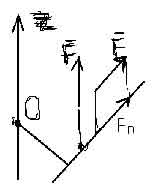
б) hп = 0 (сила пересекает ось)
Момент силы относительно оси = 0, если сила и ось находятся в одной плоскости.
Момент сил относительно декартовых осей координат (проекции момента силы на эти оси).
| i j k |
M0(F) = r * F = | x y z | = (y*Fz - z*Fy)*i + (z*Fx - x*Fz)*j + (x*Fy - y*Fx)*k = Mox(F)*i + Moy(F)*j + Moz(F)*k
| Fx Fy Fz |
Mox(F)=y*Fz - z*Fy
Moy(F)=z*Fx - x*Fz
Moz(F)=x*Fy - y*Fx
Связь векторного момента силы относительно точки с моментом силы относительно оси, проходящей через эту точку.
2*S(OA'B') = 2*S(OAB)*cosα
| Moz(F) | = | Mo(F) |*cosα
MCOO = проекции на эту ось векторному МСОТ
