Рассмотрим изменение вектора b(t) по отношению к двум системам координат — подвижной O'XYZ и неподвижной Oxyz.
Абсолютной, или полной, производной вектора b по аргументу t назьшается вектор 
определяющий изменение вектоpa b(t) в неподвижной системе Oxyz.
Относительная, или локальная, производная 
определяет измененине вектора b(t) в подвижной системе O'XYZ.
Формула Бура (получается из зависимости между полной и локальной производными):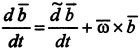 
.
Рассомтрим частные случаи.
1) угловая скорость = 0, то = ;
2) вектор b не меняется в подвижной системе отсчета ( =0), то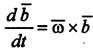 
;
3) 
, т.е. вектор b все время параллелен вектору угловой скорости (
), то = . В частности, если 
, то 
, т.е. вектор угловой скорости изменяется одинаково для подвижной и неподвижной систем координат.
Дополнение:
Выведение формулы Бура:
Найдем зависимость между полной и локальными производными. Если воспользоваться проекциями вектора b(t) на оси подвижной системы O'XYZ, то можно записать: 
, где I, J, К — орты, не изменяемые в этой системе отсчета. Поэтому локальная производная 
, а полная производная с учетом изменения также ортов I, J, К имеет вид: 
. В правой части уравнения первые три слагаемых выражают локальную производную, а производные от ортов I, J, K определяются формулами Пуассона (
), т.е. 
. С учетом получаем: .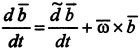
Скорости и ускорения точки при сложном движении.
ρ = r0 + r
dp/dt = d(r0+r)/dt = dr0/dt + dr/dt
dp/dt = v0 + dr/dt + ω*r = v0 + vr + ω*r
v = v0 + ω*r + vr = ve + vr
a = dv/dt = d(v0 + ω*r +vr)/dt = a0 + (dω/dt)*r + ω*(dr/dt) + dvr/dt
dr/dt = d(~)r/dt + ω*r = vr + ω*r
dvr/dt = d(~)vr/dt + ω*vr = ar + ω*vr
a = a0 + ε*r + ω*vr + ω*vr + ω*(r*ω) + ar + ω*vr = a0 + a(вр) + ω*vr + ω*vr + а(ос) + ar + ω*vr
a = a0 + ε*r + ω*(r*ω) + ar + + 2*ω*vr, где 2*ω*vr - добавочное (поворотное) ускорение, a0 + ε*r + ω*(r*ω) - (ае) переносное ускорение.
Ускорение Кориолиса. Правило Жуковского.
Кинематическая теорема Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений - относительного, переносного и ускорения Кориолиса.
Ускорение Кориолиса равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки: 
, следовательно по модулю ускорение Кориолиса: 
(sin90=1).
Кориолисово ускорение обращаетсяв нуль, когда: 1) переносное движение - поступательное, т.е. омега переносное равно нулю; 2) в те моменты времени, когда в относительном движении точка останавливается, например. при изменении направления относительного движения.
Правило Жуковского: Кориолисово ускорение можно получить, спроецировав вектор радиальной скорости на плоскость, перпендикулярную вектору омега переносное, увеличив полученную проекцию радиальной скорости в 2*(омега переносное) раз и повернув ее на 90 градусов в направлении переносного вращения.
