Определение скоростей точек плоской фигуры с помощью МЦС.
Если мгновенный центр скоростей Р найден и если известна угловая скорость фигуры, то скорость любой точки В фигуры определяется как скорость этой точки во вращательном движении вокруг МЦС, т. е. вектор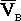 
перпендикулярен к отрезку РВ и по модулю равен w×РВ. Отсюда следует, что скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е.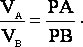 
Соотношение между ускорениями двух точек плоской фигуры при плоском движении.
т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении плоской фигуры вокруг полюса.
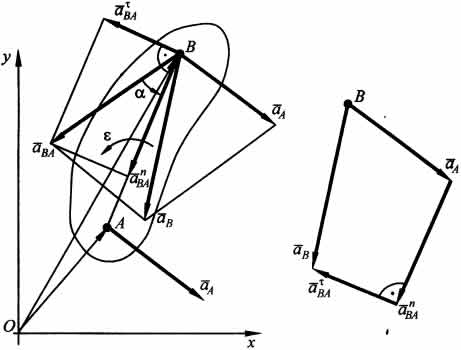
Ускорение точки В вокруг А состоит из касательной и нормальной составляющих: 
, модули которых 
.
Касательное ускорение направлено перпендикулярно отрезку АВ в сторону, указанную дуговой стрелкой углового ускорения.Нормальное ускорение направлено от точки В к полюсу А. Таким образом,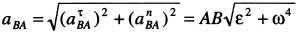 
.
Обозначив угол между ускорением точки В вокруг А и отрезком АВ через "альфа", найдем: 
.
Способы определения углового ускорения при плоском движении.
т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении плоской фигуры вокруг полюса.
Ускорение точки В вокруг А состоит из касательной и нормальной составляющих: , модули которых .
Касательное ускорение направлено перпендикулярно отрезку АВ в сторону, указанную дуговой стрелкой углового ускорения.Нормальное ускорение направлено от точки В к полюсу А. Таким образом, .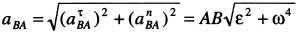
Обозначив угол между ускорением точки В вокруг А и отрезком АВ через "альфа", найдем: .
Мгновенный центр ускорений (МЦУ). Способы нахождения.
При определении скоростей точек плоской фигуры было установлено, что в каждый момент времени существует такая точка Р фигуры (МЦС), скорость которой равна нулю. Покажем, что в каждый момент времени существует точка фигуры, ускорение которой равно нулю. Такая точка называется мгновенным центром ускорений (МЦУ). Обозначим ее через Q.
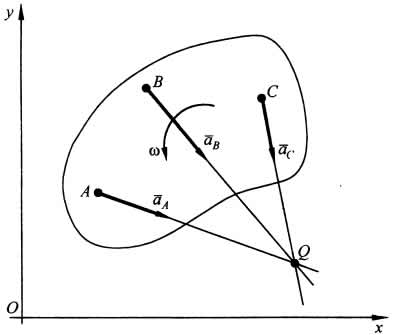
Рассмотрим плоскую фигуру, совершающую движение в плоскости рисунка (рис.). Примем за полюс какую-либо точку А, модуль и направление ускорения аА которой известны в рассматриваемый момент времени. Пусть в этот момент времени известны угловая скорость и угловое ускорение фигуры. Из формулы следует, что точка Q будет МЦУ, если 
, т. е. когда 
. Так как вектор aQA составляет с линией AQ угол "альфа" 
, то параллельный ему вектор аА направлен к линии, соединяющей полюс А с точкой Q, также под углом "альфа" (см. рис.).
Проведем через полюс А прямую MN, составляющую с вектором его ускорения угол "альфа", откладываемый от вектора аА в направлении дуговой стрелки углового ускорения. Тогда на луче AN найдется точка Q, для которой . Поскольку, согласно , 
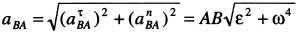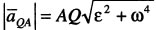, точка Q (МЦУ) будет отстоять от полюса А на расстоянии 
.
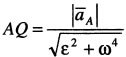Таким образом, в каждый момент движения плоской фигуры, если угловая скорость и угловое ускорение не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. В каждый последующий момент времени МЦУ плоской фигуры будет находиться в различных ее точках.
Если МЦУ — точку Q выбрать за полюс, то ускорение любой точки А плоской фигуры
, так как aQ = 0. Тогда 
. Ускорение аА составляет с отрезком QA, соединяющим эту точку с МЦУ, угол "альфа", откладываемый от QA в сторону, противоположную направлению дуговой стрелки углового ускорения. Ускорения точек фигуры при плоском движении пропорциональны расстояниям от МЦУ до этих точек.
Таким образом, ускорение всякой точки фигуры при ее плоском движении определяется в данный момент времени так же, как и при вращательном движении фигуры вокруг МЦУ.
Рассмотрим случаи, когда положение МЦУ можно определить с помощью геометрических построений.
1) Пусть известны направления ускорений двух точек плоской фигуры, ее угловые скорость и ускорение. Тогда МЦУ лежит на пересечении прямых линий, проведенных к векторам ускорений точек фигуры под одним и тем же острым углом: 
, отложенным от векторов ускорений точек в направлении дуговой стрелки углового ускорения.
2) Пусть известны направления ускорений хотя бы двух точек плоской фигуры, ее угловое ускорение = 0, а угловая скорость не равна 0. 
3) Угловая скорость= 0, угловое ускорение не равно 0. Угол прямой. 
