РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 14

Тема: «Неразрезные балки»

Цель работы:

Построение эпюр поперечных сил изгибающих моментов для неразрезной балки

Студент должен знать:

1. методику определения поперечных сил в произвольном сечении балки;
2. методику определения изгибающих моментов в произвольном сечении балки.

Студент должен уметь:

1. составлять и применять уравнения трех моментов;
2. строить эпюры поперечных сил и изгибающих моментов.

Вопросы для самоконтроля:

1. Напишите уравнение трех моментов.
2. Напишите уравнения трех моментов для опоры № 2 пятипролетной, четырехпролетной балок.
3. Объясните построение суммарной эпюры изгибающих моментов.
4. Как определить максимально изгибающий момент в пролете неразрезной балки с равномерно распределенной нагрузкой.
5. Как строится эпюра моментов от пролетных нагрузок?
6. Как строится эпюра опорных моментов?
7. Как определить поперечную силу в каждом пролете неразрезной балки?
8. Как по эпюре поперечных сил вычислить опорные реакции балки?

 

Методические указания

1. Обозначить пролеты и опоры на заданной схеме (системе): первый пролет — l₁ второй — l₂ третий — l ₃ и т. д. Первая опора обозначается О, вторая — 1, третья — 2 и т.д.

2. От заданной системы перейти к основной системе. Для этого каждую опору заменяют шарниром и опорным моментом, который замещает действие отброшенной связи. Опорные моменты обозначают М₀, М₁, М₂,... в зависимости от номера опоры. Величина этих моментов неизвестна.

Если балка имеет консоль, то в основной системе она отбрасывается, а действие отброшенных сил, приложенных к консоли, учитывается. Если одна из крайних опор жестко защемляющая, то в основной системе ее заменяют шарнирной опорой и добавляют еще один пролет и опору, которые называют фиктивными, так как в заданной системе их нет. Длина фиктивного пролета принимается равной нулю. Если защемляющая опора расположена на левом конце, то фиктивный пролет обозначают 1 ₀ = О, а фиктивную опору — «—1» (минус первая) и опорный момент М_-1 = О. Если защемляющая опора расположена на правом конце, то фиктивному пролету, опоре и моменту присваивается индекс, следующий за индексом предшествующего пролета (опоры, момента).

3. Определить значения изгибающих моментов от заданной на грузки для основной системы в каждом пролете. По найденным значениям строят эпюру моментов от заданной нагрузки для основной системы, которую обозначают М .

4. Определить неизвестные опорные моменты с помощью уравнений трех моментов, которые составляются для каждой промежуточной опоры. Во всех задачах самостоятельной работы основная система имеет одну промежуточную опору, в задачах расчетно-графической работы — две. Поэтому в этих задачах составляются соответственно одно и два уравнения трех моментов.

Для балки, у которой в заданной системе все опоры шарнирные или одна (правая) защемляющая, уравнения трех моментов имеют вид:

для первой промежуточной опоры 1

для второй промежуточной опоры 2

где М₁ и М₂ — опорные моменты на промежуточных опорах, их определяют путем решения уравнений; М₀ и М₃ — опорные моменты на концевых опорах, их находят по схеме балки; А , А , В , В — фиктивные опорные реакции для основной системы (по прил. 4).

Если защемляющая опора расположена слева, то, учитывая все дополнительные преобразования (см. п. 2), уравнения трех моментов принимают вид:

для первой промежуточной опоры 0

для второй промежуточной опоры 1

где М₀ и М₁ — опорные моменты на промежуточных опорах, их определяют путем решения уравнений; М_-1 и М₂ — опорные моменты на крайних опорах, их определяют по схеме балки; В , А , В , А — фиктивные опорные реакции для основной системы (по прил. 4). В примерах они условно показаны на основной системе. Решают уравнения и определяют опорные моменты.

5. По найденным значениям построить эпюры опорных моментов М_оп, откладывая их на соответствующих опорах с учетом полученных знаков и соединяя прямыми линиями.

6. Определить значения изгибающих моментов М_х от заданной нагрузки для заданной системы путем суммирования значения эпюр М и М_оп в характерных точках или способом (подвешивания эпюр). По найденным значениям строят эпюру М_х.

7. Определить значения поперечных сил Q_у на опорах по формулам

на n-ой опоре:

;

; т.е.

где Q и Q — значения поперечной силы на i -й опоре (i = 0, 1, 2), соответственно чуть левее и чуть правее ее;

А , В , А , В , А , — опорные реакции для простой балки (см. прил. VI);

М₀, М₁, М₂, М₃ — найденные ранее опорные моменты.

Поперечные силы на участках между опорами и на консольных участках определяются по общим правилам. По найденным значениям строят эпюру Q_х, используя зависимости между нагрузкой и характером эпюры Q_х.

В качестве проверки можно найти сумму моментов всех левых или правых сил (и опорных реакций в том числе) относительно любой точки балки. Они должны быть равны между собой.

Пример 1, а. Построить эпюру М_х для неразрезной балки.

Решение

1. Обозначить пролеты 1₁ и 1₂ и опоры 0, 1, 2 (рис.42, а).

2. От заданной системы перейти к основной, введя на каждую опору шарниры и опорные моменты (рис. 42,6).

3. Определить изгибающие моменты в характерных точках для основной системы от заданной нагрузки (см. прил. 5). Момент в точке С под силой F₁ = 80 кН

момент в точке D под силой F₂ = 30 кН

По найденным значениям строим эпюру М (рис.42, в).

а

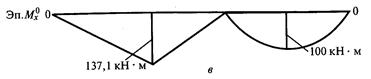
рис. 42

4. Составить уравнение трех моментов. Промежуточная опора одна, поэтому и уравнение для опоры 1 будет одно:

где М₀ = 0, так как опора 0 концевая и шарнирная;

= 151,1 кН×м.

Подставим числовые значения в уравнение моментов:

0+2 М ₁ (7 + 5) – 22,5 × 5 = - 6 (251,4 + 151,1)

или 24М₁ = 2302, откуда М₁ = — 95,9 кН×м.

В точке С величина опорного момента

В точке D величина опорного момента

5. По найденным значениям построить эпюру М_оп (рис. 42, г).

6. Суммировать значения эпюр М и М_оп в характерных точках:

По найденным значениям строим эпюру М_х (рис.42, д).

7.По формулам ( см. методические указания ) вычислить поперечные силы в характерных точках.

1. По найденным значениям построить эпюру поперечных сил.

Пример 1, б. Построить эпюру М_х для балки, показанной на рис. 43, а.

Решение

1. Обозначить опоры 0, 1 и пролет 1 ₁ (рис. 43, а).

2. От заданной системы перейти к основной. Для этого вместо опор О и 1 вводим шарниры и опорные моменты М₀ и М₁. Кроме того, влево от опоры О вводим дополнительный (фиктивный) пролет 1 ₀ = О и фиктивную опору —1 с опорным моментом М_-1 = О (рис. 43, 6).

3. Определить величины изгибающих моментов в характерных точках для основной схемы от заданной нагрузки (см. прил. 5).

Моменты в точках С и D от силы F₁

Момент в точке Е (середине пролета) от нагрузки q

Момент в точке Е от совместного действия силы F₁ и нагрузки q равен сумме моментов от каждого из них:

 

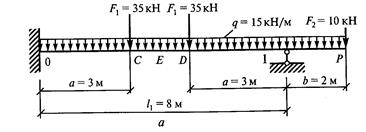
рис. 43

Значения М и М можно не определять, так как они меньше М . Строим эпюру М (рис. 43, в).

4. Составить уравнение трех моментов для промежуточной опоры 0:

где М_-1 =0, так как и опора, и момент фиктивные; l ₀ = 0, так как этот пролет тоже фиктивный;

Подставим числовые значения в уравнение трех моментов:

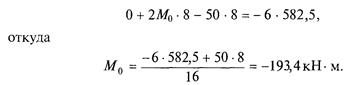
5. Построить эпюру опорных моментов М_оп (рис. 43, г). Значение опорного момента в середине пролета (точка Е)

6. Определить значение изгибающего момента от заданной нагрузки для заданной схемы в точке Е:

Строим эпюру М_х (рис. 43, д). Она должна быть уточнена после построения эпюры Q_х,

7.По формулам ( см. методические указания ) вычислить поперечные силы в характерных точках.

8. По найденным значениям построить эпюру поперечных сил.

Задание для расчетно-графической работы № 14. Построить эпюры изгибающих моментов и поперечной силы для неразрезной балки по данным одного из вариантов.

 

рис. 11