Основные формулы
Момент инерции относительно оси вращения:
А) материальной точки  , где
, где  - масса материальной точки,
- масса материальной точки, 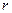 - расстояние материальной точки от сои вращения.
- расстояние материальной точки от сои вращения.
Б) дискретного твердого тела  ,
, 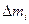 - масса
- масса  -го элемента,
-го элемента,  - его расстояние до оси вращения
- его расстояние до оси вращения
В) сплошного твердого тела 
Если тело однородно, то его плотность одинакова по всему объему и 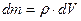
Моменты инерции некоторых тел правильной геометрической формы
| Тело | Ось, относительно которой определяется момент инерции | Формула момента инерции |
Однородный тонкий стержень массы  и длиной и длиной 
| Проходит через центр тяжести стержня перпендикулярно стержню | 
|
Тонкое кольцо, обруч радиусом 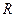 и массой и массой 
| Проходит через центр перпендикулярно плоскости кольца | 
|
Однородный шар массой  и радиусом и радиусом 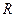
| Проходит через центр шара | 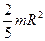
|
Теорема Штейнера позволяет рассчитать момент инерции тела относительно произвольной оси  , где
, где  - момент инерции тела относительно оси, проходящей через центр масс параллельно данной оси;
- момент инерции тела относительно оси, проходящей через центр масс параллельно данной оси;  - расстояние между осями;
- расстояние между осями;  - масса тела
- масса тела
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение и запишите формулу, определяющую момент инерции материальной точки. Единицы измерения.
2. Дайте определение и запишите формулу, определяющую момент инерции системы материальных точек.
3. Дайте определение и запишите формулу, определяющую момент инерции сплошного твердого тела.
4. Сформулируйте теорему Штейнера.
5. Дайте определение центра масс.
6. Запишите формулы, определяющие координаты центра масс.
7. Запишите формулы для моментов инерции твердых тел:
8. От каких величин и как зависит угловое ускорение согласно основному уравнению вращательного движения тела?
9. Поясните физический смысл понятия «момент инерции тела».
| Тело | Ось, относительно которой определяется момент инерции | Формула момента инерции |
Однородный длинный стержень массой m и длиной 
| А)Проходит через центр масс стержня перпендикулярно стержню | |
Б)проходит через точку, отстоящую на  от конца стержня, перпендикулярно стержню от конца стержня, перпендикулярно стержню
| ||
| Тонкое кольцо массой m и радиусом R | А) проходит через центр кольца перпендикулярно его плоскости Б) проходит через середину радиуса перпендикулярно плоскости кольца | |
| Круглый однородный диск радиусом R и массой m |  а)Проходит через центр диска перпендикулярно плоскости диска
б)относительно оси а)Проходит через центр диска перпендикулярно плоскости диска
б)относительно оси 
| |
| Однородный шар массой m и радиусом R | Проходит через центр шара |
ЗАДАЧИ
1. Определить момент инерции материальной точки массой 20 г, находящейся на расстоянии 30 см от оси вращения.
2. Два маленьких шарика массой  каждый скреплены тонким невесомым стержнем длиной
каждый скреплены тонким невесомым стержнем длиной  . Определить момент инерции системы относительно оси, перпендикулярной к стержню и проходящей через центр масс.
. Определить момент инерции системы относительно оси, перпендикулярной к стержню и проходящей через центр масс.
3. Определить момент инерции шара относительно оси, совпадающей с касательной к его поверхности. Радиус шара  , его масса
, его масса  .
.
4. Чему равен момент инерции тонкого прямого стержня длиной  и массой
и массой  относительно оси, перпендикулярной к его длине и проходящей через точку стержня, которая удалена на
относительно оси, перпендикулярной к его длине и проходящей через точку стержня, которая удалена на  от одного из его концов?
от одного из его концов?
5. Три маленьких шарика массами  каждый расположены в вершинах равностороннего треугольника со стороной
каждый расположены в вершинах равностороннего треугольника со стороной  и скреплены между собой. Определить момент инерции системы относительно оси, перпендикулярной плоскости треугольника и проходящей через центр описанной окружности. Массами стержней, соединяющих шарики, пренебречь.
и скреплены между собой. Определить момент инерции системы относительно оси, перпендикулярной плоскости треугольника и проходящей через центр описанной окружности. Массами стержней, соединяющих шарики, пренебречь.
6. Вычислить момент инерции молекулы этилена относительно осей ох и оу, если 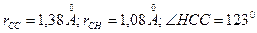 .
.
7. Вычислить момент инерции плоской прямоугольной пластины со сторонами  и
и 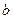 относительно оси, проходящей через центр тяжести перпендикулярно плоскости пластины.
относительно оси, проходящей через центр тяжести перпендикулярно плоскости пластины.
8. Вычислить момент инерции квадрата массой  со стороной
со стороной  относительно оси, совпадающей с его диагональю.
относительно оси, совпадающей с его диагональю.
9.  Вычислить момент инерции проволочного прямоугольника со сторонами
Вычислить момент инерции проволочного прямоугольника со сторонами  относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью
относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью  .
.
10. Однородный диск радиуса  имеет круглый вырез. Масса заштрихованной части диска равна
имеет круглый вырез. Масса заштрихованной части диска равна  . Найти момент инерции такого диска относительно оси, перпендикулярной к плоскости диск и проходящей через точку О.
. Найти момент инерции такого диска относительно оси, перпендикулярной к плоскости диск и проходящей через точку О.
11. Как изменится момент инерции свинцового цилиндра радиусом 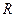 и высотой
и высотой  относительно его оси, если цилиндр сплющить в диск толщиной
относительно его оси, если цилиндр сплющить в диск толщиной  ?
?
12. Выведите формулу для момента инерции цилиндрической муфты относительно оси, совпадающей с ее осью симметрии. Масса муфты равна  , внутренний радиус
, внутренний радиус 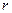 , внешний радиус
, внешний радиус 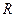 .
.
13. Найти момент инерции тонкой однородной пластины массы  относительно оси, проходящей через одну из вершин пластины перпендикулярно к ее плоскости, если стороны пластины равны длиной 40 см., как это показано на рисунке.
относительно оси, проходящей через одну из вершин пластины перпендикулярно к ее плоскости, если стороны пластины равны длиной 40 см., как это показано на рисунке.
14. 
 Два шара массами
Два шара массами  и
и  (
( закреплены на тонком невесомом стержне Определить моменты инерции системы.относительно оси, перпендикулярной стержню и проходящей через его конец в этих случаях. Размерами шаров пренебречь.
закреплены на тонком невесомом стержне Определить моменты инерции системы.относительно оси, перпендикулярной стержню и проходящей через его конец в этих случаях. Размерами шаров пренебречь.
15. Найти момент инерции прямоугольного треугольника массой 6 кг относительно оси, совпадающей с одним из катетов, если другой катет равен 60 см.
16. На рис АС- диагональ прямоугольника  . Во сколько раз момент инерции треугольника
. Во сколько раз момент инерции треугольника  больше момента инерции треугольника
больше момента инерции треугольника  относительно оси
относительно оси 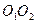 , совпадающей со стороной АВ?
, совпадающей со стороной АВ?
17. Два однородных тонких стержня: АВ длиной  и массой
и массой  и
и 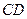 длиной
длиной  и массой
и массой 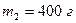 скреплены под прямым углом. Определить момент инерции системы стержней относительно оси
скреплены под прямым углом. Определить момент инерции системы стержней относительно оси  , проходящей через конец стержня АВ параллельно стержню
, проходящей через конец стержня АВ параллельно стержню 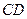 .
.
18.  На концах тонкого однородного стержня длиной
На концах тонкого однородного стержня длиной  и массой
и массой  прикреплены маленькие шарики массами
прикреплены маленькие шарики массами 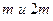 . Определить момент инерции системы относительно оси, проходящей через точку О, лежащую на оси стержня. Вычисления выполнить для случаев, изображенных на рисунке. Шарики рассматривать как материальные точки.
. Определить момент инерции системы относительно оси, проходящей через точку О, лежащую на оси стержня. Вычисления выполнить для случаев, изображенных на рисунке. Шарики рассматривать как материальные точки.
СЕМИНАР 9






