Рассмотрим колебательную систему, состоящую из точечного груза массы 
и четырех связанных с ним пружин. Если масса движется по гладкой горизонтальной поверхности (на рисунке показан вид сверху), то ее мгновенное расположение описывается двумя смещениями из положения равновесия (точки О) - 
и 
. Говорят, что такая система обладает двумя степенями свободы. Если колебания являются гармоническими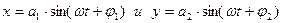 
, то уравнение траектории движения шарика можно получить следующим образом. Перепишем уравнения колебаний в виде: 
Умножим первое уравнение на 
, а второе – на 
и вычтем из первого уравнения второе, получим
. (1)
Умножим первое уравнение на 
, а второе – на 
и вычтем из первого уравнения второе, получим
. (2)
Возведем в квадрат каждое из равенств (1) и (2) и сложим их, получим
(3)
В общем случае груз будет совершать периодические движения по эллиптическим траекториям. Направление движения вдоль траектории и ориентация траектории зависят от начальной разности фаз 
.
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Каковы результаты сложения двух взаимно перпендикулярных гармонических колебаний одной и той же частоты, кратных частот? Каков будет результат при соотношении частот: а) 1:2; 2) 1:3?
ЗАДАЧИ
1. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 
. Найти уравнение траектории, построить ее и указать направление движения..
2. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 
. Найти уравнение траектории, построить ее и указать направление движения..
3. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями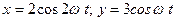 
. Найти уравнение траектории, построить ее и указать направление движения..
4. Складываются два гармонических колебания одного направления с одинаковыми периодами 
и амплитудами 
. Начальные фазы колебаний 
. Определить амплитуду и фазу результирующего колебания, найти его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд.
5. Складываются два гармонических колебания одного направления с одинаковыми периодами и амплитудами 
. Начальные фазы колебаний 
. Определить амплитуду и фазу результирующего колебания, найти его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд.
6. Складываются два гармонических колебания одного направления с одинаковыми периодами и амплитудами 
. Начальные фазы колебаний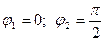 
. Определить амплитуду и фазу результирующего колебания, найти его уравнение и построить с соблюдением масштаба векторную диаграмму сложения амплитуд.
7. Сложить с помощью векторной диаграммы и аналитически два колебания 
и 
.одинаково направленных колебаниях
8. Точка участвует в двух одинаково направленных колебаниях 
и 
. Определить амплитуду результирующего колебания, его частоту и начальную фазу колебаний. Найти уравнение движения. Построить векторную диаграмму.
9. Складываются два гармонических колебания одинаковой частоты и одинакового направления: 
и 
. Начертить векторную диаграмму для момента времени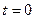 
. Определить аналитически амплитуду и начальную фазу результирующего колебания. Отложить результирующую амплитуду и фазу на векторной диаграмме. Найти уравнение результирующего колебания (в тригонометрической форме через косинус). Задачу решить для двух случаев: 1) 
2) 
.
10. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями 
и 
. Найти уравнение траектории точки и построить график траектории. Указать на графике точку, соответствующую началу движения.
11. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: 1) 
; 2) 
; 3) 
; 4) 
; 5) 
; 6) 
; 7) 
; 8) 
. Найти для восьми случаев уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: 
. По
12. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям и описываемых уравнениями: 
; 2) 
; 3) 
; 4) 
. Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.
Семинар 14
