Задания
К практическим занятиям по механике
Для студентов химического факультета
В.А.Жукова
Самара 2013
Семинар 1
Кинематика поступательного движения. Средняя скорость.
 Основные формулы
Основные формулы
Положение материальной точки в пространстве в момент времени  определяется радиус-вектором
определяется радиус-вектором  (рис.1)
(рис.1)
Средняя скорость 
Средняя путевая скорость  , где
, где  -путь, пройденный точкой за интервал времени
-путь, пройденный точкой за интервал времени 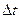 .
.
Мгновенная скорость 
В декартовой системе координат  ,
,
Модуль вектора перемещения 
Тогда скорость  ,
,
Следовательно компоненты скорости даются формулами 
Модуль вектора скорости 
Мгновенное ускорение  ,
,
компоненты ускорения могут быть выражены 
модуль вектора ускорения 
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что изучает механика как один из разделов физики?
2. Что такое тело отсчета?
3. Что такое система отсчета?
4. Что такое радиус-вектор?
5. Дайте определения кинематических величин: перемещения, пройденного пути, средней скорости, мгновенной скорости, среднего ускорения, мгновенного ускорения. В каких единицах измеряются эти величины?
6. Как ориентированы векторы скорости (мгновенной и средней) и ускорения относительно траектории и друг друга?
7. Какое движение абсолютно твердого тела называется поступательным?
8. Как можно вычислить пройденный путь, если задан график зависимости скорости от времени?
9. Приведите примеры, когда Землю можно представить как материальную точку и когда этого сделать нельзя.
10. Как найти результирующее перемещение точки, если известны составляющие перемещения, в которых она участвует?
11. Какие Вам известны способы задания законов движения?
ЗАДАЧИ
1. Автомобиль половину пути движется со скоростью  , а вторую половину пути – со скоростью
, а вторую половину пути – со скоростью  . Найти среднюю путевую скорость автомобиля.
. Найти среднюю путевую скорость автомобиля.
2. Автомобиль половину времени движется со скоростью  , а вторую половину времени – со скоростью
, а вторую половину времени – со скоростью  . Найти среднюю путевую скорость автомобиля.
. Найти среднюю путевую скорость автомобиля.
3. Положение материальной точки на оси х в зависимости от времени задано уравнением  . Найти среднюю скорость точки на временном интервале от
. Найти среднюю скорость точки на временном интервале от  . Сравнить полученное значение с мгновенными скоростями
. Сравнить полученное значение с мгновенными скоростями  и
и  в моменты времени
в моменты времени  и
и  соответственно.
соответственно.
4. Кинематическое уравнение движения материальной точки по прямой имеет вид  . Найти: 1) максимальное значение координаты; 2)момент времени, когда точка возвращается в то же место, где она была в начальный момент времени. Построить график зависимости от времени координаты и пути, пройденного точкой с момента
. Найти: 1) максимальное значение координаты; 2)момент времени, когда точка возвращается в то же место, где она была в начальный момент времени. Построить график зависимости от времени координаты и пути, пройденного точкой с момента  до
до  .
.
5.  Материальная точка движется в плоскости согласно уравнениям
Материальная точка движется в плоскости согласно уравнениям  и
и  . Найти модули скорости и ускорения точки в момент времени
. Найти модули скорости и ускорения точки в момент времени 
6. Точка движется вдоль оси х согласно графику, изображенному на рисунке. Построить графики изменения ускорения и скорости движения. Определить начальную и среднюю скорость движения.
7. Материальная точка движется прямолинейно с начальной скоростью  и с постоянным ускорением
и с постоянным ускорением  . Определить, чему равен путь, пройденный точкой, и модуль ее перемещения спустя 4 с после начала движения.
. Определить, чему равен путь, пройденный точкой, и модуль ее перемещения спустя 4 с после начала движения.
8. Автомобиль едет по прямой из пункта А в пункт В, преодолевая это расстояние за  . Известно, что скорость автомобиля меняется по закону
. Известно, что скорость автомобиля меняется по закону 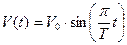 , где время t отсчитывается с момента выезда из пункта А, а максимальная скорость автомобиля
, где время t отсчитывается с момента выезда из пункта А, а максимальная скорость автомобиля  . Определить среднюю путевую скорость автомобиля и расстояние между пунктами А и В.
. Определить среднюю путевую скорость автомобиля и расстояние между пунктами А и В.
9. Скорость реки  , а скорость движения лодки относительно воды
, а скорость движения лодки относительно воды  . Определить, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки.
. Определить, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки.
10. Капля дождя при скорости ветра 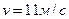 падает под углом
падает под углом  к вертикали. Определите, при какой скорости ветра капля воды будет падать под углом
к вертикали. Определите, при какой скорости ветра капля воды будет падать под углом  .
.
11. Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного пути дается уравнениями  и
и  . Определите относительную скорость автомобилей.
. Определите относительную скорость автомобилей.
12. Автомобиль проехал первую половину времени своего движения со скоростью  , вторую половину времени своего движения – со скоростью
, вторую половину времени своего движения – со скоростью  Определите среднюю скорость движения автомобиля.
Определите среднюю скорость движения автомобиля.
13. Автомобиль проехал первую половину пути своего движения со скоростью  , вторую половину пути своего движения – со скоростью
, вторую половину пути своего движения – со скоростью  Определите среднюю скорость движения автомобиля.
Определите среднюю скорость движения автомобиля.
14. В течение времени  скорость задается уравнением вида
скорость задается уравнением вида 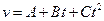 . Определить среднюю скорость за указанный промежуток времени.
. Определить среднюю скорость за указанный промежуток времени.
15. Материальная точка движется по плоскости согласно уравнению  . Написать зависимости:
. Написать зависимости: 
16. Движение точки по прямой задано уравнением  . Определить среднюю скорость движения точки в интервале времени от t1=1 c до t2=3 c.
. Определить среднюю скорость движения точки в интервале времени от t1=1 c до t2=3 c.
17. Частица движется в плоскости х,у из точки с координатами х=у=0 со скоростью  , где а и b – некоторые постоянные. Найти уравнение её траектории.
, где а и b – некоторые постоянные. Найти уравнение её траектории.
18. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид  . Построить график зависимости координаты х и пути от времени. Определить среднюю скорость за интервал времени от 1 с до 6 с.
. Построить график зависимости координаты х и пути от времени. Определить среднюю скорость за интервал времени от 1 с до 6 с.
19. Движение материальной точки в плоскости ху описывается законом  , где А и В – положительные постоянные. Определите: 1) уравнение траектории; 2) радиус-вектор точки в зависимости от времени; 3) скорость точки в зависимости от времени; 4) ускорение точки в зависимости от времени.
, где А и В – положительные постоянные. Определите: 1) уравнение траектории; 2) радиус-вектор точки в зависимости от времени; 3) скорость точки в зависимости от времени; 4) ускорение точки в зависимости от времени.
20. Зависимость пройденного телом пути 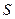 от времени
от времени  дается уравнением
дается уравнением  . Найти: 1) зависимость скорости и ускорения от времени; 2) расстояние, пройденное телом, скорость и ускорение через 2 с после начала движения
. Найти: 1) зависимость скорости и ускорения от времени; 2) расстояние, пройденное телом, скорость и ускорение через 2 с после начала движения
21. Кинематические уравнения движения двух материальных точек имеют вид: x1=-2t2, x2=2t+t3. Определить момент времени, для которого ускорения этих точек будут равны.
22. Зависимость пройденного точкой пути от времени задана уравнением  (здесь и далее, если не оговорено особо, время измеряется в секундах, расстояние в метрах. Определить: 1) через какое время ускорение точки будет равно
(здесь и далее, если не оговорено особо, время измеряется в секундах, расстояние в метрах. Определить: 1) через какое время ускорение точки будет равно  ; 2) мгновенную скорость в этот момент времени; 3) среднюю путевую скорость за промежуток времени от
; 2) мгновенную скорость в этот момент времени; 3) среднюю путевую скорость за промежуток времени от  .
.
23. Положение точки на прямой в зависимости от времени дается уравнением  . Сравнить ее со средними скоростями
. Сравнить ее со средними скоростями  на интервале от
на интервале от 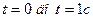 и
и  на интервале
на интервале  .
.
24. Две материальные точки движутся согласно уравнениям  . В какой момент времени ускорения этих тел будут одинаковы? Найти скорости точек в этот момент времени.
. В какой момент времени ускорения этих тел будут одинаковы? Найти скорости точек в этот момент времени.
25. Движение двух материальных точек заданы уравнениями  . В какой момент времени скорости этих точек будут одинаковы? Определить скорости и ускорения точек в этот момент.
. В какой момент времени скорости этих точек будут одинаковы? Определить скорости и ускорения точек в этот момент.
26. Зависимость пройденного телом пути от времени дается уравнением  . Найти расстояние, пройденное телом, скорость и ускорение тела через 2 с после начала движения.
. Найти расстояние, пройденное телом, скорость и ускорение тела через 2 с после начала движения.
Семинар 2
Кинематика вращательного движения
Основные формулы
Тангенциальное ускорение точки  , где
, где  - линейная скорость точки
- линейная скорость точки
Нормальное (центростремительное) ускорение-  , где
, где  - радиус кривизны траектории
- радиус кривизны траектории
Полное ускорение  .
.
Средняя угловая скорость 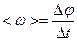 , где
, где  -изменение угла поворота за интервал времени
-изменение угла поворота за интервал времени 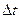
Мгновенная угловая скорость  , где
, где  -угол поворота радиус-вектора.
-угол поворота радиус-вектора.
Угловое ускорение 
Кинематическое уравнение равномерного вращения  , где
, где  - начальное угловое перемещение,
- начальное угловое перемещение,  - время
- время
При равномерном вращении 
Для равномерного вращательного движения  , где
, где  -период обращения,
-период обращения,  - частота обращения, то есть число оборотов в единицу времени
- частота обращения, то есть число оборотов в единицу времени 
Угловая скорость связана с линейной скоростью движения соотношением 
Кинематическое уравнение равнопеременного вращательного движения (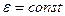 )
) 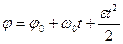 , где
, где  - начальная угловая скорость
- начальная угловая скорость
Угловая скорость тела при равнопеременном вращении 
Тангенциальное и нормальное ускорения при вращательном движении могут быть выражены следующим образом 
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Покажите на рисунке направление мгновенной скорости, нормального и тангенциального ускорения.
2. Дайте определение периода обращения.
3. Как связан период обращения с линейной частотой?
4. Дайте определение угловой скорости и запишите формулу, выражающую смысл этого понятия.
5. Дайте определение углового ускорения.
6. Как связаны линейная и угловая скорость?
7. Запишите связь углового и линейного ускорения.
8. Что называется тангенциальным и нормальным ускорениями? Чему они равны?
9. Запишите связь между угловым ускорением и угловой скоростью при равномерном движении по окружности.
ЗАДАЧИ
1. Нормальное ускорение точки, движущейся по окружности радиусом  задается уравнением
задается уравнением 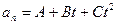 (где
(где  ). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за 5 с после начала движения; 3) полное ускорение для момента времени
). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за 5 с после начала движения; 3) полное ускорение для момента времени  .
.
2. Материальная точка начинает двигаться по окружности радиусом  с постоянным тангенциальным ускорением
с постоянным тангенциальным ускорением  . Определите: 1) момент времени, при котором вектор ускорения образует с вектором скорости угол
. Определите: 1) момент времени, при котором вектор ускорения образует с вектором скорости угол  ; 2) путь, пройденный за это время движущейся точкой.
; 2) путь, пройденный за это время движущейся точкой.
3. Колесо вращается с постоянным угловым ускорением  . Определите радиус колеса, если через
. Определите радиус колеса, если через  после начала движения полное ускорение колеса равно
после начала движения полное ускорение колеса равно  .
.
4. Якорь электродвигателя, имеющий частоту вращения  , после выключения тока, сделав
, после выключения тока, сделав  оборотов, остановился. Определите угловое ускорение якоря.
оборотов, остановился. Определите угловое ускорение якоря.
5. Колесо автомашины вращается равнозамедленно. За 2 минуты оно изменило частоту вращения от  до
до  . Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
6. Точка движется по окружности радиусом  с постоянным тангенциальным ускорением. К концу четвертого оборота после начала движения линейная скорость точки
с постоянным тангенциальным ускорением. К концу четвертого оборота после начала движения линейная скорость точки 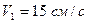 . Определите нормальное ускорение точки через
. Определите нормальное ускорение точки через  после начала движения.
после начала движения.
7. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота диска от времени задается уравнением  . Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) тангенциальное, нормальное и полное ускорение диска для точки, находящейся на расстоянии 80 см от оси вращения.
. Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) тангенциальное, нормальное и полное ускорение диска для точки, находящейся на расстоянии 80 см от оси вращения.
8. Диск радиусом 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, задается уравнением  . Определите угол, который образует вектор полного ускорения с радиусом колеса через2 с после начала движения.
. Определите угол, который образует вектор полного ускорения с радиусом колеса через2 с после начала движения.
9. Найти радиус вращающегося колеса, если известно, что линейная скорость v1 точки, лежащей на ободе, в 2,5 раза больше линейной скорости v2 точки, лежащей на 5 см ближе к оси колеса.
10. Колесо, вращаясь равноускоренно, достигло угловой скорости  рад/сек через N=10 об после начала вращения. Найти угловое ускорение колеса.
рад/сек через N=10 об после начала вращения. Найти угловое ускорение колеса.
11. Колесо, вращаясь равнозамедленно, при торможении уменьшило свою скорость за 1 мин с 300 об/мин до 180 об/мин. Найти угловое ускорение колеса и число оборотов, сделанных им за это время.
12. Точка движется по окружности радиусом R=10 см с постоянным тангенциальным ускорением 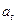 . Найти тангенциальное ускорение
. Найти тангенциальное ускорение 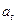 точки, если известно, что к концу пятого оборота после начала движения скорость точки стала
точки, если известно, что к концу пятого оборота после начала движения скорость точки стала 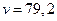 см/сек.
см/сек.
13. Колесо радиусом R=10 см вращается с постоянным угловым ускорением  . Найти для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость, 2) линейную скорость, 3) тангенциальное ускорение, 4) нормальное ускорение, 5) полное ускорение и 6) угол, составляемый направлением полного ускорения с радиусом колеса.
. Найти для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость, 2) линейную скорость, 3) тангенциальное ускорение, 4) нормальное ускорение, 5) полное ускорение и 6) угол, составляемый направлением полного ускорения с радиусом колеса.
14. Точка движется по окружности так, что зависимость пути от времени дается уравнением  ,где A=5 м, B=-2 м/сек и C=1 м/сек2. Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через t=3 сек после начала движения, если известно, что нормальное ускорение точки при t’=2 сек равно
,где A=5 м, B=-2 м/сек и C=1 м/сек2. Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через t=3 сек после начала движения, если известно, что нормальное ускорение точки при t’=2 сек равно  .
.
15. Колесо радиусом R=10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе колеса, от времени движения дается уравнением  ,где A=3 см/сек2 и B=1 см/сек2. Найти угол, составляемый вектором полного ускорения с радиусом колеса в моменты времени t=0,1,2,3,4 и 5 сек после начала движения.
,где A=3 см/сек2 и B=1 см/сек2. Найти угол, составляемый вектором полного ускорения с радиусом колеса в моменты времени t=0,1,2,3,4 и 5 сек после начала движения.
16. Небольшое тело начинает движение по окружности радиусом 30 см с постоянным по модулю тангенциальным ускорением  . Найти полное ускорение через 3 с после начала движения.
. Найти полное ускорение через 3 с после начала движения.
17. Материальная точка движется по окружности радиусом 5 м. Когда нормальное ускорение точки становится равным  , угол между векторами полного и нормального ускорений равен
, угол между векторами полного и нормального ускорений равен  . Найти модули скорости и тангенциального ускорения точки для этого момента времени.
. Найти модули скорости и тангенциального ускорения точки для этого момента времени.
18. Нормальное ускорение точки, движущейся по окружности радиусом 3,2 м, изменяется по закону  . Найти: а) путь, пройденный частицей за 5 с после начала движения; б) тангенциальное и полное ускорение в конце этого участка пути.
. Найти: а) путь, пройденный частицей за 5 с после начала движения; б) тангенциальное и полное ускорение в конце этого участка пути.
19. По окружности радиусом 5 м равномерно движется материальная точка со скоростью  . Построить графики зависимости длины пути и модуля перемещения от времени. Считать, что в начальный момент времени перемещение равно нулю.
. Построить графики зависимости длины пути и модуля перемещения от времени. Считать, что в начальный момент времени перемещение равно нулю.
20. Диск радиусом 20 см вращается согласно уравнения точек на окружности диска  . Определить тангенциальное, нормальное и полное ускорение для момента времени
. Определить тангенциальное, нормальное и полное ускорение для момента времени  .
.
Семинар 3






