Аналитическое выравнивание имеет своей конечной целью получение конкретного уравнения связи между двумя сопряженными признаками. В первую очередь исходные данные наносят на систему координат и по характеру расположения точек определяют функцию для выравнивания. Её график должен проходить максимально близко по отношению ко всем исходным точкам. В данном примере характер расположения точек линейный следовательно выравнивание осуществляем по уравнению прямой.
Как известно, уравнение линейной зависимости общего вида будет иметь вид: y = а x+b.
Вычисление конкретного уравнения сводится к определению числовых значений коэффициентов а, b, для получения которых существует несколько способов. Рассмотрим два, наиболее широко применяемых способа, характеризующихся различной точностью и трудоемкостью:
а) способ координат двух избранных точек, обеспечивающий получение менее точных результатов, но гораздо более простым путем;
б) способ наименьших квадратов, позволяющий получить достаточно точные результаты путем использования координат всех выравниваемых точек (наблюдений).
Остановимся на технике работ при вычислении конкретного уравнения методом координат избранных точек. В этом случае исходные данные изображаются на графике, и производится предварительное выравнивание. Результирующая линия проводится между точками с таким расчетом, чтобы разделить их общее количество на две приблизительно равные части. При этом необходимо стремиться к такому положению, чтобы расстояние между линией и исходными точками было кратчайшим. Для облегчения техники выравнивания и увеличения его точности можно рекомендовать следующий прием. Соединить все выравниваемые точки и постараться провести плановую выравнивающую линию по возможности ближе к этим серединам. При этом желательно провести прямую таким образом, чтобы хотя бы две исходные точки попали на неё. С полученной прямой линии снимаем координаты двух любых точек исходных данных (лежащих на проведенной прямой). Если число наблюдений в классах известно, то следует отдать предпочтение точкам, обеспеченным наибольшим числом наблюдений. В нашем примере в качестве избранных использованы координаты точек классов № 2 и № 6.
X2=16; Y2=18,00; X6=32; Y6=23,65.
Система двух конкретных уравнений приобретет вид
После подстановки координат избранных точек:
После решения системы относительно а и b, получим
а=0,35 b=12,4
Следовательно, полученное конкретное уравнение связи Y/Х (Д/Н) будет иметь вид
у=0,35x+12,4
Для краткости изложения в последующем тексте полученным уравнениям присвоены определенные номера: уравнение, вычисленное методом координат точек, получает номер I, а уравнение, полученное методом наименьших квадратов – номер II.
Пределы «работы» полученного уравнения по диаметру от 10 см до 46 см.
Рассмотрим технику вычислений при использовании способа наименьших квадратов. Для получения конкретного уравнения в этом случае используются координаты всех точек. Это учитывается при выведении системы уравнений для этого метода. Так, если записать уравнения прямой для каждой точки, а потом просуммировать левые и правые части всех уравнений, то получим следующее:
y1= ax1 + b
y2= ax2 + b
y3= ax3 + b
……………
……………
∑y=a∑x+bn.
Так как нам необходимо найти два неизвестных значения (a и b), то в системе должно быть два уравнения. Для получения второго уравнения системы умножим обе части каждого уравнения на соответствующий «х» и просуммируем левые и правые части уравнений. Получим:
x1y1= ax12 + bх1
x2y2= ax22 + bx2
x3y3= ax32 + bx3
….……………
….……………
∑хy=a∑x2+b∑х.
Таким образом, мы вывели оба уравнения системы:
Для удобства вычислений числовых значений указанной системы составляется вспомогательная таблица (табл.4.2).
Таблица 4.2
Вспомогательные расчеты для вычисления конкретного уравнения
прямой линии
| Исходные данные | ХY | Х2 | |
| Х | Y | ||
| 16,00 | 192,00 | ||
| 18,00 | 288,00 | ||
| 20,15 | 403,00 | ||
| 22,14 | 531,36 | ||
| 23,48 | 657,64 | ||
| 23,65 | 756,80 | ||
| 24,62 | 886,32 | ||
| 26,00 | 1040,00 | ||
| 27,00 | 1188,00 | ||
 252
| 201,04
| 5943,12
| 8016
|
Подставим итоговые данные в систему уравнений и вычислим коэффициенты а, b, имея в виду, что значение «n» соответствует числу классов по X:
Следовательно, конкретное уравнение будет иметь вид
Y=0,33Х+13,1
С целью последующего анализа результатов применения полученных уравнений вычисляются вероятные (теоретические) значения зависимого признака по первому уравнению (yв1) и второму уравнению (yв2). Последние (yв2) сравниваются с исходными (опытными) данными (у). Указанные сравнения (a = y–yв2) производятся по всем классам X, а их результат для прямой линии показан в табл. 4.3.
Таблица 4.3
Сравнение исходных и вероятных высот деревьев, полученных по уравнению прямой линии
| Исходные данные | Вероятные высоты | Отклонения, м | ||
| диаметр, см | высота, м | Ув1 | Ув2 | a = y–yв2 |
| X | Y | |||
| 16,00 | 16,60 | 17,06 | -1,06 | |
| 18,00 | 18,00 | 18,38 | -0,38 | |
| 20,15 | 19,40 | 19,70 | +0,45 | |
| 22,14 | 20,80 | 21,02 | +1,12 | |
| 23,48 | 22,20 | 22,34 | +1,14 | |
| 23,65 | 23,60 | 23,66 | -0,01 | |
| 24,62 | 25,00 | 24,98 | -0,36 | |
| 26,00 | 26,40 | 26,40 | -0,40 | |
| 27,00 | 27,80 | 27,62 | -0,62 | |
| ∑-0,12 |
Приведенные данные позволяют, прежде всего, проверить правильность вычислений, выполненных при получении конкретных уравнений, на предмет обнаружения грубых арифметических ошибок.
Правильность вычисления уравнений связи проверяется путем сравнения исходных значений Y с вероятными (ув), полученными по уравнению I (ув1) и уравнению II (ув2) Критерием правильности вычислений уравнения I будет совпадение вероятных значений ув1 с исходными значениями Y для тех классов, в которых использованы координаты точек в качестве исходных для получения конкретного уравнения I. В нашем примере для уравнения прямой линии значение ув1 равно 18,0, соответствует исходным данным Y во втором классе, то есть также 18,0. Аналогичное положение и в следующем, шестом классе: ув1 =23,6 практически не отличается от Y =23,65. Совпадение Y и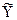 
в остальных классах не обязательно и может наступить только случайно.
Некоторый контроль правильности уравнения II можно получить путем сопоставления Y и ув2 – во всех классах. В этом случае должно наблюдаться такое сочетание знаков (плюс и минус), которое отражает «срединное» положение выравнивающей прямой между выравниваемыми исходными значениями Y.
О явной неправильности полученного уравнения будет свидетельствовать наличие во всех классах только +, равно как и знаков -, а также, если в нескольких начальных классах будут наблюдаться отклонения с одним и тем же знаком (+ или -), а во всех последующих классах с противоположным, а именно:
+++++++
- - - - - - -
++++- - -
- - - -+++
Заметим, что описанные критерии правильности и вычислений I и II уравнений распространяются и на выравнивание по всем другим линиям связи.
