Первое представление о наличии или отсутствии корреляционной связи, ее форме и направленности дает графическое изображение данных наблюдения. Если выборка малая, то в систему координат зависимости Y от X наносятся все исходные данные. При большой выборке график строится по средним значениям классов Wх - и условно средним значениям – уср (рис. 3.1).
Вывод об отсутствии связи делается в том случае, если при изменении значений х уср практически остается на одном уровне, т.е. не изменяется (рис. 3.1 а), или изменчивость уср слишком велика и не может быть выражена математически (рис. 3.1 б). Если через полученные на графике точки можно провести прямую линию, то зависимость между признаками признается линейной (рис. 3.1 в, г).

Рис. 3.1 Графическое изображение корреляционных связей для большой выборки (а, б – связь отсутствует; в – связь линейная, прямая; г – связь линейная обратная; д, е– связь нелинейная)

Рис. 3.2 Корреляционная зависимость между диаметрами и поперечниками крон 125 деревьев сосны (прямая)
В рассматриваемом примере для большой выборки зависимость между поперечниками крон и диаметрами деревьев сосны, судя по графику (рис. 3.2), можно предварительно считать линейной, прямой.
Вычисление показателей тесноты связи и их оценка при большой выборке.
Если по графику удалось определить форму связи, то сразу приступают к вычислению показателей ее тесноты: коэффициенту корреляции – r или корреляционному отношению - η. Иногда установить форму связи по графику затруднительно, тогда этот вопрос решается математически, путем вычисления меры линейности – Z и ее оценки.
Вспомогательные расчеты
Прежде чем приступить к вычислению показателей тесноты корреляционной связи, необходимо предварительно вычислить среднее значение и среднеквадратическое отклонение по каждому из признаков X и Y. Сделать это можно при помощи начальных моментов. Вычисление этих показателей для рассматриваемого примера большой выборки представлено в табл. 3.3 и 3.4.
Таблица 3.3
Вычисление Mx, σx

| 
| А | 
| аnx | а2 | a2nx | Вычисления |
| -3 | -12 | 



| |||||
| -2 | -16 | ||||||
| -1 | -22 | ||||||
| Итого | -50 +86 +36 |
Условные обозначения:
А – условное начало;
ν1 – первый начальный момент;
ν2 – второй начальный момент.
Таблица 3.4
Вычисление Мy, σy

| 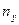
| А | а | а·ny | а2 | a2 ny | Вычисления |
| 1,5 | -3 | -18 | 



| ||||
| -2 | -24 | ||||||
| 2,5 | -1 | -21 | |||||
| 3,5 | |||||||
| 4,5 | |||||||
| Итого | +24 |






