Общеизвестно, что в природе все взаимосвязано и взаимообусловлено и, следовательно, изменение одного признака какого-либо явления неизбежно ведет к изменению других. Так, с увеличением возраста дерева увеличивается его высота, диаметр, длина листьев, корней, толщина коры, объем ствола и т.д. Это свойство природы широко используется в практике лесного хозяйства, когда по значению одного из признаков, обычно легко доступного для обмера, приходится рассчитывать значение другого признака, определение величины которого связано со значительными трудностями.
Особенностью массовых явлений в природе является их изменчивость, варьирование, поэтому связи, наблюдающиеся в природе, не так очевидны. Каждому значению одного признака здесь может соответствовать несколько значений другого признака. Обнаруживаются такие связи только при достаточно большом числе наблюдений. Обычно эти связи принято называть корреляционными.
От корреляционных надо отличать известные в математике функциональные связи, при которых каждому значению независимой переменной соответствует только одно, строго определенное значение второй переменной. В связи с этим пределами корреляционной связи является полное отсутствие связи между признаками, когда с изменением одного признака второй не изменяется, и наличие функциональной связи, когда зависимость между признаками может быть выражена математически.
Корреляцию называют простой, если она измеряется на основе двух признаков, или множественной, когда на результативный признак влияет несколько факторов. По форме корреляция может быть линейной и нелинейной, по направлению - прямой и обратной.
Учитывая вышесказанное, при проведении корреляционного анализа решаются следующие задачи:
1. Установление факта наличия или отсутствия связи между изучаемыми признаками.
2. Определение формы связи, и ее направленности.
3. Вычисление показателя тесноты связи и его оценка.
Исходные данные, построение корреляционной таблицы
Исходные данные для проведения простого корреляционного анализа при большой и малой выборках представлены двумя рядами цифр. В качестве примера рассмотрим данные большой выборки по обмеру диаметров и соответствующих им поперечников крон у 125 деревьев сосны (табл. 3.1).
Таблица 3.1
Данные обмера диаметров и поперечников крон деревьев сосны*
(фрагмент)
| Номер дерева | Диаметр на высоте груди, см (х) | Поперечник кроны, м (y) |
| 17,4 | 2,1 | |
| 25,2 | 3,2 | |
| 21,0 | 2,9 | |
| · | · | · |
| 31,0 | 4,1 |
* В целях сокращения приведены начало и конец таблицы
Для удобства обозрения и анализа, особенно при большой выборке, данные наблюдений систематизируют, т.е. строят таблицу распределения или, как ее иначе называют, корреляционную таблицу.
При этом из двух изучаемых признаков за "X" принимают тот, который легко определяется в натуре.
Перед построением корреляционной таблицы так же, как и при построении вариационного ряда, делаются вспомогательные расчеты. При этом для каждого из признаков отдельно определяется максимальная Vmax и минимальная (Vmin) варианты и размер ряда (р.р.), который будет равен Vmax -Vmin. Количество классов принимается равным от 8 до 12. Величина интервала ( ) определяется как частное от деления размера ряда на количество классов. Для вычисления среднего значения начального класса к минимальной варианте прибавляют половину интервала. Желательно, чтобы средние значения классов (W) и величина интервала были числами целыми или, если это невозможно, удобными дробными (чётными). Количество классов по каждому признаку может быть разным.
) определяется как частное от деления размера ряда на количество классов. Для вычисления среднего значения начального класса к минимальной варианте прибавляют половину интервала. Желательно, чтобы средние значения классов (W) и величина интервала были числами целыми или, если это невозможно, удобными дробными (чётными). Количество классов по каждому признаку может быть разным.
После определения средних значений классов (Wx и Wy) и их границ производят разноску вариант методом точковки сразу по двум признакам. При этом в таблицу для каждого дерева ставится одна точка на пересечении соответствующих классов по признаку X и по признаку Y, к которым относится данное дерево. Итоги такой разности для рассматриваемого примера показаны в табл. 3.2.
Таблица 3.2
Корреляционная таблица для установления связи между диаметрами (X) и поперечниками крон (Y) деревьев сосны
Wy
| Поперечники крон (y), м | Итого nx | Условно- средний поперечник кроны yср | ||||||||
| 1,5 | 2,5 | 3,5 | 4,5 | ||||||||
| Диаметры (х), см |  3 3
|  1 1
| 1,625 | ||||||||
 2 2
|  5 5
|  1 1
| 1,94 | ||||||||
 1 1
|  5 5
|  11 11
|  4 4
|  1 1
| 2,48 | ||||||
 1 1
|  7 7
|  21 21
|  9 9
|  2 2
| 3,05 | ||||||
 2 2
|  5 5
|   13 13
|  4 4
|  1 1
| 3,44 | ||||||
 2 2
| 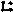 6 6
|  7 7
|  2 2
| 3,76 | |||||||
 1 1
|  3 3
|  4 4
|  1 1
| 4,28 | |||||||
| Итого ny |
В конце таблицы для каждого из классов по признаку X вычисляется условно среднее значение уср,. Например, в первом классе диаметров, равном 12 см, имеется 4 дерева. Три дерева из них имеют поперечник кроны, равный 1,5 и, а одно дерево – 2 м. Следовательно, условно-среднее значение уср =(3x1,5м)+(1х2м):4=1,625 м. Аналогичным образом вычисляются условно-средние значения для остальных классов диаметров.





 Wx
Wx