В задании с помощью моментов получают четыре статистических показателя: среднюю величину признака (М), основное отклонение (σ), показатели косости (К) и крутости (i) вариационного ряда.
Применительно к нашему примеру перечисленные показатели вычисляются следующим образом:
 см
см

Значения М и σ, полученные с использованием моментов, не отличаются от результатов вычислений этих же величин, определенных способом непосредственных вычислений. Допускаемая величина расхождения при правильных вычислениях не должна превышать предела округления; в нашем примере для:
М - до 0,05 см, для σ - 0,005 см.
Напомним, что в данном случае получено одинаковое именованное значение основного отклонения (σ = 6,89 см). Основное отклонение, выраженное в относительных единицах (σ), т.е. в долях интервала (единицах разряда), в нашем примере можно определить двумя путями:
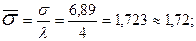
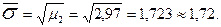
Показателем косости (асимметрии) вариационного ряда (К) служит величина третьего основного момента (r 3).
В правильных (симметричных) вариационных рядах место класса с максимальной частотой (модальный класс) находится в середине (центре) ряда. Частоты классов, расположенных по обе стороны от центрального класса, приблизительно одинаковы. Такие ряды симметричны и косости не имеют: К = r 3 = 0.
В асимметричных рядах места модального и центрального классов не совпадают. Кривые распределений, отображающие такие рады имеют неодинаковые ветви, по направлению которых судят о характере асимметрии. При смещении модального класса влево от центрального длина правой ветви превышает длину левой. Это дает основание констатировать правостороннюю асимметрию, которая считается также и положительной, поскольку величина К. будет со знаком плюс. При смещении модального класса вправо будет иметь место левосторонняя отрицательная асимметрия при отрицательном значении К.
Косость ряда также оценивается и по величине; при К <±0,5 косость считается малой, при К от ±0,5 до ±1,0 – средней, при К. >±1,0 – большой.
Крутость вариационных рядов, или кривых их отображающих, оценивается по характеру распределения частот в классах. В сравнении с нормальными теоретическими распределениями практические ряды могут быть плосковершинными (туповершинными) или островершинными (высоковершинными).
Плосковершинные ряды лишены четко выраженного модального класса, частоты центральных классов имеют близкие значения, пределы ряда ограничены. В островершинных рядах имеется характерный максимум из одного или нескольких классов, пределы ряда несколько расширены за счет классов с малыми частотами.
Объективная оценка крутости (i) производится по формуле i = r 4 - 3. Если у нормальных рядов i = 0 (r 4 = 3), то при i > 0 ряд считается островершинным (эксцесс кривой), при i < 0 - низковершинным (дефект кривой).
Оценка косости и крутости практического ряда, рассматриваемого в нашем примере, будет следующей.
Оценка косости: поскольку К = r = +0,25, вариационный ряд имеет малую положительную (правую) асимметрию.
Оценка крутости: поскольку i = r 4 -3 = 2,89 - 3 = -0,11 вариационный ряд является плосковершинным.
Полученные показатели косости и крутости вычислениями по формулам не контролируются.
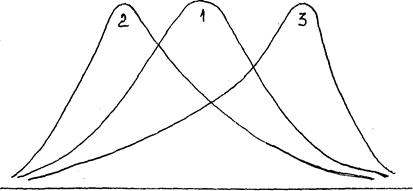
Рис. 2.1 Виды асимметрии рядов:
1 - симметричный (правильный); 2 - правосторонняя; 3 - левосторонняя
Критерием правильности вычислений этих показателей может служить оценка характера распределения частот отдельных классов, что сравнительно легко выполняется при анализе кривой по графикам (рис. 2.1 и 2.2).
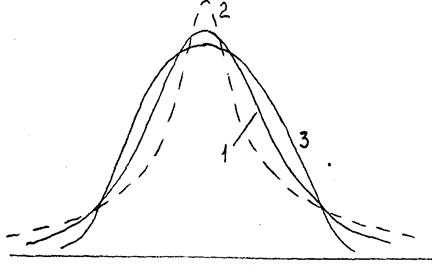
Рис. 2.2 Крутость рядов распределения:
1 - правильный ряд; 2 - островершинный ряд (эксцесс); 3 - туповершинный ряд (дефект).






