Как указывалось выше если по графику выявлен нечеткий характер корреляционной связи (линейная или нелинейная), то уточнение характера связи производится математически. С этой целью по величинам r и η определяют меру линейности (z), ее основную ошибку (
) и так называемый показатель Блекмана (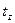
) – показатель достоверности меры линейности. Мера линейности определяется по формуле:
Для рассматриваемого примера зависимости поперечников кроны от диаметров на высоте груди мера линейности будет равна;
;
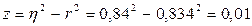ошибка меры линейности ():
;
показатель Блекмана:
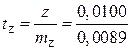=1,12 < t0.05=2.0
t0,05 – показатель Стьюдента, при вероятности 0,05 равен 2. Так как tZ<t0,05 , следовательно, связь между признаками нужно признать линейной. Данный признак подтверждает и предварительно выявленный по графику линейный характер связи.
Линейное корреляционное уравнение
После установления характера и тесноты корреляционной связи необходимо получить математическую модель исследуемой зависимости в виде уравнения связи. Если связь нелинейная, то необходимо подобрать функцию, график которой будет максимально приближен ко всем исходным точкам, а если линейная – то получить конкретное уравнение прямой.
В данной работе, независимо от того какой характер связи получится фактически, будем рассчитывать уравнение прямой, условно принимая, что связь между исследуемыми признаками линейная. Для этого необходимо преобразовать исходное уравнение прямой:
Подставив в приведенное выше уравнение все известные значения (My, r, σy, σx, Mx) неизвестными останутся только х и у:
В результате преобразований: у=3,1+0,1112x–2,798
получим конкретное уравнение прямой:
уx = 0,1112х + 0,3
Далее заполняется таблица (табл. 3.7) для построения графика. При этом значения yx рассчитываются по найденному выше конкретному уравнению прямой.
Таблица 3.7
| Х (Wx) | |||||||
| yср | 1,625 | 1,94 | 2,48 | 3,05 | 3,44 | 3,76 | 4,28 |
| yx | 1,63 | 2,08 | 2,52 | 2,97 | 3,41 | 3,86 | 4,3 |
| yср–yx | -0,005 | -0,14 | -0,04 | 0,08 | 0,03 | -0,1 | -0,02 |
На графике изображаются исходные данные (yср) в виде отдельных точек и вероятные (yx – найденные по рассчитанному уравнению) – в виде прямой (рис. 3.3).
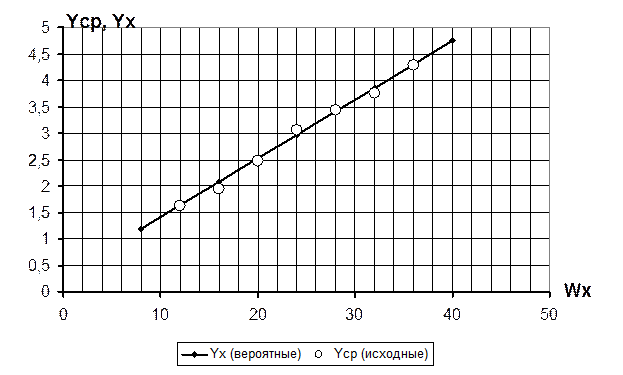
Рис. 3.3 Графическое изображение корреляционной связи.
4. РЕГРЕССИОННЫЙ АНАЛИЗ
Техника и способы регрессионного анализа
В качестве примера для аналитического выравнивания используются данные взаимосвязи двух сопряженных признаков: диаметров (Д), принимаемых за X, и высот деревьев (H), принимаемых за Y.
Таблица 4.1
Взаимосвязь диаметров и высот (невыравненные данные)
| № классов | |||||||||
| Д (X), см | |||||||||
| H (Y) м | 16,00 | 18,00 | 20,15 | 22,14 | 23,48 | 23,65 | 24,62 | 26,00 | 27,00 |
