Получение статистических показателей

СПОСОБОМ НЕПОСРЕДСТВЕННЫХ ВЫЧИСЛЕНИЙ

ПО ИСХОДНЫМ ФОРМУЛАМ

 

Для вычисления основных статистических показателей среднего значения признака (М) и основного отклонения (σ) производятся вспомогательные расчеты, показанные в табл. 2.1.

Таблица 2.1

Вспомогательные расчёты для получения среднеарифметической величины

(М) и основного отклонения (σ) способом непосредственных вычислений

W	n	Wn	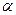M	= W - M
				-15,4	-46,2	237,16	711,48
				-11,4	-159,6	129,96	1819,44
				-7,4	-214,6	54,76	1588,04
				-3,4	-139,6	11,56	473,96
			31,4	+0,6	+32,4	0,36	19,44
				+4,6	+147,2	21,16	677,12
				+8,6	+172,2	73,96	1479,20
				+12,6	+126,0	158,76	1587,60
				+16,6	+66,4	275,56	1102,24
				+20,6	+20,6	424,36	424,36
					-559,8 +564,6 +4,8		9882,88

 

 

Среднее (среднеарифметическое) значение признака получают по формуле:

где: W- значение класса, n.- частота класса, N - численность ряда.

В нашем примере см

Контроль правильности вычисления M:

: = 4,8: 208 = 0,023 < 0,05

 

Во избежание ошибок в последующих вычислениях полученное значение М подлежит контролю. Приближенный контроль можно выполнить следующим образом: вероятное значение М должно быть близко к значению класса с максимальной частотой. Для точного контроля необходимо использовать сумму произведений отклонений значений классов (W) от округленной среднеарифметической величины (М), т.е.:

,

умножив данные отклонения на частоты (n) соответствующих классов (). При правильно вычисленной и округленной величине М должно наблюдаться следующее соотношение между величиной и пределом округления М, величина которого в нашем примереравна 0,05:

Напомним, что если значение М записано с точностью до целой величины, то пределом ее округления будет 0,5; при записи М с точностью до 0,1; 0,01; 0,001 пределами округления соответственно будут 0,05; 0,005; 0,0005.

После вычисления и контроля М определяется величина медианы (Ме) и моды (Мо).

Величина медианы соответствует значению варианты, занимающей срединное место в вариационном ряду последовательного суммирования. Поскольку численность исследуемого ряда равна 208, то следует установить значение диаметра, приближенно соответствующее 104-ой или 105-ой варианте. Медиана определяется по формуле:

,

где: К - левая граница класса, в котором находится половина накопленных частот

Sk - накопленная частота по границе К;

n - частота данного класса.

В нашем примере:

см

Может быть использован график, на котором изображена огива (рис.1.1). На оси ординат для накопленных частот () находят точку, соответствующую указанной варианте (например, 104), восстанавливают из нее перпендикуляр до пересечения с огивой и из этой точки опускают перпендикуляр до пересечения с осью абсцисс, по которой и отсчитывают искомое значение медианы. В нашем примере Мe = 31,2 см.

Приближенное значение моды соответствует значению класса с максимальной частотой, а именно:

Мo = W_maх = 32 см.

Точное значение моды определяют по формуле:

Мо ⁼ 3 Mе - 2 M

В нашем примере:

Мo = 3×31,2 - 2×31,4 = 93,6 - 62,8 = 30,8 см.

Для контроля вычислений следует помнить, что в правильных, с симметричными ветвями вариационных рядах значения М, Мe, Мo близки между собой.

Приведенные ниже вычисления остальных статистических показателей не требуют особых разъяснений.

Среднеквадратическое (основное) отклонение (σ) вычисляют по формуле:

 

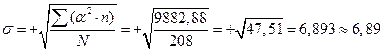см

 

Коэффициент изменчивости (варьирования):

Основная ошибка среднего значения признака:

см

Ошибка основного отклонения:

Ошибка меры изменчивости:

Показатель достоверности среднего значения признака:

Показатель точности исследования (опыта):

 

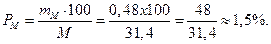
Полученные значения статистических показателей подлежат контрольной проверке. Так, величина σ проверяется через значение С. Коэффициент вариации признаков в специально подобранных для студентов заданиях, как правило, не превышает 30-40 %. Величина m_м, контролируется через t_м и P_м Полученные средние значения признаков должны быть достоверны (t_M >3), а точность исследований - достаточно высокой (Р_м,<5-10 %).