Одной из наиболее эффективных оценок значимости уравнения регрессии является коэффициент детерминации. Он характеризует степень выраженности связи между переменными. Определяется по формуле:
. (2.35)
Величина R2 показывает, какая доля вариации зависящей переменной обусловлена вариацией объясняющей переменной. Так как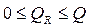 
, то 
.
Свойства коэффициента детерминации:
1. При 
регрессия хорошо отражает эмпирические данные, наблюдения примыкают к линии регрессии.
2. При 
точки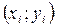 
лежат на линии регрессии и между переменными существует линейная функциональная зависимость.
3. При 
вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных и линия регрессии параллельна оси ОХ.
Если известен коэффициент детерминации R2, то критерий значимости уравнения регрессии
(2.36)
В случае линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции.
Оценка статистической значимости коэффициентов парной линейной регрессии и корреляции.
В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: 
и 
.
Стандартная ошибка коэффициента регрессии определяется по формуле:
, (2.38)
где 
– остаточная дисперсия.
Величина стандартной ошибки совместно с 
-распределением Стьюдента при 
степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой. Определяется фактическое значение -критерия Стьюдента 
, которое затем сравнивается с табличным значением при определенном уровне значимости 
и числе степеней свободы . Доверительный интервал для коэффициента регрессии определяется как 
, этот процесс был описан в § 2.3.3.
Стандартная ошибка параметра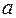 
определяется по формуле:
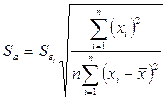. (2.39)
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется -критерий: 
, его величина сравнивается с табличным значением при 
степенях свободы.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции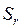 
:
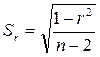. (2.40)
Фактическое значение 
-критерия Стьюдента определяется как 
.
Существует связь между -критерием Стьюдента и 
-критерием Фишера:
.
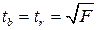