Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Таким образом, мы имеем здесь набор объясняемых переменных, связанных через уравнения системы. Системы одновременных уравнений требуют относительно более сложный математический аппарат. Используются в макроэкономике.
Рассмотрим, например,модель спроса и предложения.
Пусть QtD – спрос на товар в момент времени t,
QtS – предложение товара в момент времени t,
Pt – цена товара в момент времени t,
Yt – доход в момент времени t.
Составим следующую систему уравнений «спрос-предложение»:
QtS = α1 + α2 + α3 Pt + α3 Pt-1 + εt (предложение),
QtD = β1 + β 2 + β 3 Pt + β 3 Yt + ut (спрос),
QtS = QtD (равновесие).
Цена на товар Pt и спрос на товар QtS равный предложению QtD определяются из уравнений модели, они являются эндогенными переменными. Предопределенными (экзогенными) переменными в данной модели являются доход Yt и значение цены товара в предыдущий момент времени Pt-1.
Взаимосвязанные переменные, описывающие экономический объект, и формирующиеся внутри функционирования объекта, называются эндогенными, а задаваемые извне – экзогенными. Лаговыми переменными называются взятые в предыдущий момент времени переменные.
Типы данных при эконометрическом моделировании
Пространственные данные
Это данные в определенный момент времени. Например:
- набор сведений (объем производства, количество работников, доход и др,) по разным фирмам в один и тот же момент времени (пространственный срез);
- данные по курсам покупки/продажи наличной валюты в какой-то день по городу.
Временные ряды
Данные через определенные отрезки времени. Например:
- ежеквартальные данные по инфляции, средней заработной плате, национальному доходу, денежной эмиссии за последние годы;
- ежедневный курс доллара США, цены фьючерсных контрактов на поставку доллара США, котировки акций за ряд последних лет.
Отличительной чертой временных рядов является то, что они естественным образом упорядочены по времени, кроме того, наблюдения в близкие моменты времени часто бывают зависимыми.
Основные положения регрессионного анализа
В регрессионном анализе объясняемая переменная у представляется в виде функции
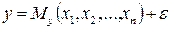, (1.15)
где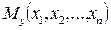 
– функция, значение которой является условным математическим ожиданием величины у, полученным при данном наборе значений объясняющих переменных (функция регрессии);
ε - случайная составляющая.
В случае парной регрессии
у = My (x) + ε. (1.16)
Для линейной парной регрессии вид модели:
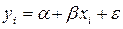, (1.17)
где (xi; yi)- элементы выборки, содержащей n пар значений переменных.
