Построенная на рис. 2.2 доверительная область для M  (x) определяет местоположение условного математического ожидания или среднего значения зависимой переменной (модельной линии регрессии), но не отдельных возможных значений зависимой переменной, которые отклоняются от средней.
(x) определяет местоположение условного математического ожидания или среднего значения зависимой переменной (модельной линии регрессии), но не отдельных возможных значений зависимой переменной, которые отклоняются от средней.
Поэтому при определении доверительного интервала для индивидуальных значений y 0зависимой переменной учитывают еще один источник вариации – рассеяния вокруг линии регрессии, то есть в оценку суммарной дисперсии  включается величина
включается величина 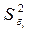 . В результате оценка дисперсии индивидуальных значений y 0при x = x 0равна
. В результате оценка дисперсии индивидуальных значений y 0при x = x 0равна
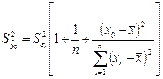 . (2.22)
. (2.22)
Соответствующий доверительный интервал для прогнозов индивидуальных значений y 0определяется по формуле:
 . (2.23)
. (2.23)
На рис. 2.2 данный доверительный интервал показан пунктиром.
15. Доверительный интервал для параметра β регрессионной модели.
Наряду с интервальными оценками функции регрессии иногда представляет интерес построения доверительных интервалов для параметров регрессионной модели 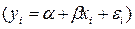 , в частности для α, β и
, в частности для α, β и 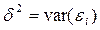 (дисперсии возмущения εi или зависимой переменной yi).
(дисперсии возмущения εi или зависимой переменной yi).
При построении доверительного интервала параметра β исходят из того, что статистика  имеет t распределение Стьюдента с
имеет t распределение Стьюдента с  степенями свободы. Интервальная оценка параметра β на уровне значимости α имеет вид:
степенями свободы. Интервальная оценка параметра β на уровне значимости α имеет вид:
 . (2.24)
. (2.24)
Поскольку знак коэффициента регрессии указывает на рост результативного признака  при увеличении признака-фактора
при увеличении признака-фактора  (
(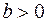 ), уменьшение результативного признака при увеличении признака-фактора (
), уменьшение результативного признака при увеличении признака-фактора (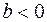 ) или его независимость от независимой переменной (
) или его независимость от независимой переменной ( ) (см. рис. 1.3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например,
) (см. рис. 1.3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например,  . Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.

Рисунок 2.3.Наклон линии регрессии в зависимости от значения параметра  .
.
Интервальная оценка параметра α на уровне значимости α имеет вид:
 . (2.25)
. (2.25)
16. Доверительный интервал для параметра σ2 регрессионной модели.
Наряду с интервальными оценками функции регрессии иногда представляет интерес построения доверительных интервалов для параметров регрессионной модели 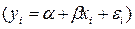 , в частности для α, β и
, в частности для α, β и 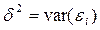 (дисперсии возмущения εi или зависимой переменной yi).
(дисперсии возмущения εi или зависимой переменной yi).
При построении доверительного интервала для параметра  исходят из того, что статистика
исходят из того, что статистика 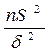 имеет
имеет  -распределение с k = n – 2 степенями свободы. Поэтому интервальная оценка для
-распределение с k = n – 2 степенями свободы. Поэтому интервальная оценка для  на уровне значимости α имеет вид:
на уровне значимости α имеет вид:
 (2.26)
(2.26)
Доверительный интервал выбирается таким образом, чтобы вероятность







