Модель парной линейной регрессии

Мы уже отмечали ранее, что если между переменными х и у существует теоретическая линейная связь в виде

y = α + βx, (2.1)

то наблюдаемые значения x_i, y_i, i =1, 2, …, n этих переменных связаны линейной моделью наблюдений

(2.2)

Если α и β – истинные значения параметров линейной модели связи, то величина ε_i = y_i - (α +βx_i) представляет собой ошибку в i -м наблюдении.

Поиск коэффициентов α и β осуществляется таким образом, чтобы величина ε стремилась к минимуму (в идеале к нулю). Если ε_i = 0, то все точки лежат на одной прямой. В результате получают подобранную модель линейной связи

.

В подобранной модели наблюдаемому значению x переменной х сопоставляется значение переменной у. Значения подобранное и реальное наблюдаемое у обычно отличаются. Разность

называется остатком в i -м наблюдении.

 

Метод наименьших квадратов оценки параметров парной регрессионной модели

Для реальных данных, как правило, все остатки отличны от нуля, так что часть из них имеет положительный знак, а остальные – отрицательный. При этом необходимо соблюдение принципа наименьших квадратов

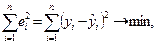
(2.5)

Получаемые при этом оценки а и b называются оценками наименьших квадратов. Свойством оценок наименьших квадратов является то, что соответствующая им прямая проходит через точку . Поиск пары чисел а и b с помощью метода наименьших квадратов (МНК) сводятся к математической задаче поиска точки минимума функции двух переменных. В результате получаем коэффициенты в подобранной модели

, (2.6) 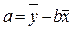, (2.7)

где

При подстановке в формулу (2.3) выражения (2.7) получаем оценку уравнения парной линейной регрессии (функция регрессии)

.

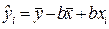Статистические свойства МНК-оценок параметров уравнения регрессии

При выполнении стандартных предположений регрессионного анализа, МНК-оценки параметров уравнения регрессии будут обладать следующими статистическими свойствами:

1. Несмещенность.

Статистическая оценка некоторого параметра называется несмещенной, если ее математическое ожидание равно истинному значению этого параметра. В случае парной линейной регрессии: М(a)=α, М(b)=ß.

2. Состоятельность.

При неограниченном возрастании объема выборки значение оценки должно стремиться по вероятности к истинному значению параметра, а дисперсии оценок параметров должны уменьшаться и в пределе стремиться к 0: , при .

3. Эффективность.

Оценка называется эффективной, если она имеет минимальную дисперсию по сравнению с другими оценками заданного класса.