Эконометрика – это совокупность методов анализа количественных связей между экономическими факторами и показателями на основании реальных статистических данных с использованием аппарата теории вероятностей и математической статистики.
Анализируя характер имеющихся статистических данных, методами эконометрики исследователь должен сделать определенные заключения о возможной форме подходящей теоретической экономической модели. Статистические данные указывают на то, в каком направлении нужно искать теоретические модели. Построение окончательной модели производится с учетом представлений экономической теории и с учетом информации, содержащейся в эмпирических данных.
Обобщенный вид эконометрической модели:
, (1.1)
где у – наблюдаемое значение зависимой переменной, (объясняемая переменная);
x 1, x 2 ,…, x 
– объясняющие переменные;
f(x 1, x 2 ,…, x ) – объясненная часть, зависящая от значений объясняющих переменных;
ε – случайная составляющая.
Рассмотрим связь между годовым располагаемым доходом х и годовыми расходами на личное потребление у (в 1999 году, в условных единицах) 20 домашних хозяйств (табл. 1.1).
Известный психолог Кейнс отметил как фундаментальный закон психологии склонность людей (как правило и в среднем), увеличивать расходы на личное потребление по мере возрастания их доходов, но не в той степени, в какой возрастает доход, то есть
y=f(x),
где обе переменные измерены в одних единицах и функция f(x) должна быть возрастающей, скорость изменения этой функции должна быть меньше 1. 
Таблица1.1
| i | x | y | i | x | y | |
Для того, чтобы установить форму функциональной связи строят диаграмму рассеяния или поле корреляции (рис. 1.1).
Простейшей моделью связи является линейная модель (модель наблюдений)
y = α + βx + ε, (1.2)
где β - некоторая постоянная величина, 0 < β <1, характеризующая в данном круге домашних хозяйств их склонность к потреблению, связанную с традиционными привычками;
α - постоянное потребление;
ε = y - (a + βx) - это отклонение реально наблюдаемых расходов на потребление уi от значения у = a + βx, предсказываемого гипотетической линейной моделью связи для i- го домашнего хозяйства.
Рисунок 1.1
В связи с наличием случайной составляющей ε точки не лежат на одной прямой, а образуют облако рассеяния.
Предложив для описания имеющихся статистических данных модель, учитывающую указанное отклонение от теоретической модели, мы должны оценить с их помощью величину параметров α и β. Затем, используя соответствующие критерии, вынести на основании этих данных суждение о пригодности выбранной модели.
2. Характеристики случайных величин: поле корреляции, математическое ожидание, среднее значение, выборочная дисперсия, стандартное отклонение.
Если в рассмотренном в предыдущем параграфе примере обозначить x 1, х 2, …, х последовательно располагаемые доходы домашних хозяйств; y 1, y 2,..., y - расходы домашних хозяйств на потребление, мы сможем говорить о наблюдаемых значениях двух этих переменных. Всего мы имеем здесь n = 20 наблюдаемых пар значений переменных х и у: (x 1; y 1), (x 2; y 2), …, (xn; yn).
Наиболее простыми показателями, характеризующими последовательности x 1, х 2, …, хn и y1, y 2,..., yn являются средние значения этих дискретных величин.
, 
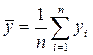. (1.3)
В рассматриваемом примере 
, 
.
Математическое ожидание дискретных случайных величин это сумма произведений всех значений дискретной величины на их вероятности, оно приближенно равно их средним значениям.
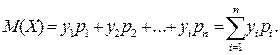(1.4)
Выборочные дисперсии (вариации) характеризуют степень разброса значений x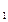 
, х 
, …х (y , y ,... y ) 
вокруг своего среднего значения 
(
)
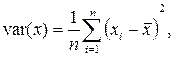
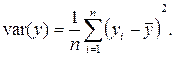(1.5)
Стандартное отклонение (среднеквадратическое отклонение) более удобно для характеристики рассеяния дискретной случайной величины, так как измеряется в тех же единицах, что и сама величина.
(1.6)
Удобным графическим средством анализа данных, является диаграмма рассеяния (поле корреляции), на которой в прямоугольной системе координат располагаются точки (xi, yi), i = 1, 2, …, n. Для того, чтобы по форме облака рассеяния делать выводы о характере зависимости между величинами при построении диаграммы желательно выбирать масштабы и интервалы изменения переменных таким образом, чтобы окно диаграммы имело вид квадрата, и чтобы на диаграмме имелись точки, достаточно близко расположенные к каждой из четырех границ этого квадрата.
3. Выборочный корреляционный момент (выборочная ковариация), коэффициент корреляции (r) и его свойства при большом объеме выборки.
Степень выраженности линейной связи между произвольными переменными х и у, принимающими значения xi, yi, i = 1, 2, …, n оценивается посредством выборочного коэффициента корреляции
, (1.7)
. (1.8)
Величина cov(x,y) называется выборочной ковариацией (выборочным корреляционным моментом). Характеризует степень зависимости двух случайных величин и степень их рассеяния.
Для расчета r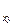 
можно использовать формулу
. (1.9)
Здесь r 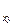находится с использованием непосредственных данных и на его значении не скажутся округления данных, связанные с расчетом средних значений.
Свойства выборочного коэффициента корреляции r 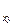(при достаточно большом объеме выборки n).
1. Коэффициент корреляции по абсолютной величине не превосходит единицы (– 1 
r 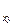1). Чем ближе 
к единице, тем теснее связь (рис. 1.2).
Рисунок 1.2
2. При r =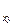 
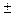1, все наблюдаемые значения лежат на одной прямой. Корреляционная связь представляет линейную функциональную зависимость
(Рис. 1.3, 1.4).
Рисунок 1.3
Рисунок 1.4
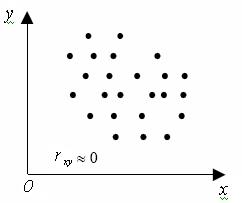
З. При r 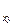= 0 линейная связь отсутствует (рис. 1.5, 1.6, 1.7)
Рисунок 1.5
