Частные коэффициенты корреляции характеризуют тесноту линейной связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
В общем виде при наличии m факторов для уравнения
(4.22)
коэффициент частной корреляции, измеряющий влияние на 
фактора 
, при неизменном уровне других факторов, можно определить по формуле:
, (4.23)
где 
– множественный коэффициент детерминации всех 
факторов с результатом; 
– тот же показатель детерминации, но без введения в модель фактора .
При двух факторах формула (4.23) примет вид:
; 
. (4.24)
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, 
– коэффициент частной линейной корреляции первого порядка. Соответственно коэффициенты парной линейной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:
.(4.25)
При двух факторах данная формула примет вид:
; 
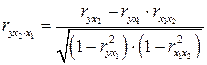. (4.26)
Для уравнения регрессии с тремя факторами частные линейные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по уравнению 
возможно исчисление трех частных коэффициентов корреляции второго порядка:
, 
, 
,
каждый из которых определяется по рекуррентной формуле. Например, при 
имеем формулу для расчета :
. (4.27)
Рассчитанные по рекуррентной формуле частные коэффициенты линейной корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты линейной корреляции дают меру тесноты связи каждого фактора с результатом в чистом виде. Если из стандартизованного уравнения регрессии 
следует, что 
, т.е. no силе влияния на результат порядок факторов таков: 
, 
, 
, то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, 
.
В эконометрике частные коэффициенты линейной корреляции обычно не имеют самостоятельного значения. Их используют на стадии формирования модели. Так, строя многофакторную модель, на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. На втором шаге отбирается фактор с наименьшей и несущественной по 
-критерию Стьюдента величиной показателя частной корреляции. Исключив его из модели, строится новое уравнение регрессии. Процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля. Если исключен несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построения регрессионной модели почти не отличаются друг от друга, 
, где m – число факторов.
Из приведенных выше формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле:
. (4.28)
В частности, для двухфакторного уравнения формула (2.16) принимает вид:
. (4.29)
При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного их влияния равен единице. Из единицы вычитается доля остаточной вариации результативного признака 
, обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.
