Ранее мы говорили о способе построения доверительного интервала на уровне значимости 
.
, (3.38)
где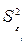 
– оценка дисперсии ошибки прогноза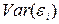 
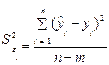, (3.39)
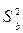– среднеквадратическое (стандартное) отклонение для b
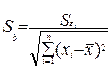(3.40)
Полученный результат показывает, что при любом истинном значении параметра 
вероятность накрытия этого значения доверительным интервалом равна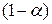 
.
Предположим, мы взяли значение 
, не принадлежащие данному интервалу. Вероятность такого события будет очень мала, меньше чем значение 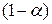. Таким образом, факт не накрытия значения, взятого значения представляет осуществление редкого события, имеющего малую вероятность, и это дает нам основание сомневаться в том, что значение параметра 
Априорные предположения о значениях параметров модели называют статистическими гипотезами.
О проверяемой гипотезе говорят как об исходной «нулевой» гипотезе и обозначают ее Н о, в нашем случае Н о: .
В соответствии со сказанным выше, такую гипотезу следует отвергать, если значение не принадлежит 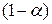-процентному доверительному интервалу. не будет принадлежать этому интервалу в том случае, если наблюдаемое значение отношения больше табличного по абсолютной величине
. (3.41)
Это означает слишком большое отклонение оценки b от гипотетического значения параметра в сравнении с оценкой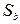 
стандартного отклонения этого параметра.
Правило решения вопроса об отклонении или не отклонении статистической гипотезы Н о, называется статистическим критерием проверки гипотезы Н о, а выбранное при формулировании этого правила значение α называется уровнем значимости критерия.
В практических исследованиях чаще всего используют,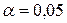 
хотя иногда и 
, 
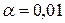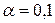и другие. Выбор большего или меньшего значения определяется степенью значимости для исследования исходной гипотезы Н о. Если мы выбираем при исследовании меньшее значение , то мы уменьшаем вероятность ошибки и вероятность отвержения верной гипотезы. Такие вероятности называют мощностью критерия.
В реальных ситуациях статистические критерии имеют довольно низкую мощность, так что рассматриваемая Н о отвергается редко, поэтому правильнее говорить о не отвержении гипотезы, а не о ее принятии.
Всякий статистический критерий основывается на использовании той или иной статистики, то есть, случайной величины, значения которой могут быть вычислены теоретически на основании имеющихся статистических данных (приближенно).
В нашем случае критерий проверки гипотезы Н о: основан на использовании t -статистики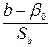 
, значение которой можно вычислить по
данным наблюдений. Критерии, основанные на использовании t -статистики (распределения) Стьюдента называют t-критериями. Каждому статистическому критерию соответствует критическое множество R значений статистики критерия, при которых гипотеза Н о отвергается в соответствии с принятыми правилами (то есть множество значений t -статистики, превышающих по абсолютной величине 
).
Таким образом, статистический критерий определяется заданием
· статистической гипотезы Н о;
· уровня значимости α;
· статистики критерия (t -статистики, χ2-статистики, F -статистики);
· критического множества R.
30. Определение и примеры моделей множественной линейной регрессии. Отбор факторов в модель множественной регрессии.
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии, где y – зависимая переменная (результативный признак), xi – независимые, или объясняющие, переменные (признаки-факторы).
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целом ряде других вопросов эконометрики. Например, потребление отдельного товара на душу населения зависит от располагаемого дохода на душу населения, цены данного товара, цен на сопутствующие товары, привлекательности товара и других факторов.
В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
+31 вопрос
