Уравнения Хартри-Фока в численной форме были решены для всех основных атомов и ионов, определен вид атомных орбиталей (АО) и их энергии. Расчет орбиталей многоатомных систем непосредственно из уравнений Хартри-Фока оказывается существенно более трудоемкой задачей, чем расчет АО атомов, из-за более низкой симметрии. Поэтому используются дальнейшие приближения. Стандартный подход состоит в том, что искомые орбитали представляют в виде:
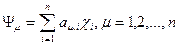(2.11)
где χi – базисные функции, вид которых зависит от расчетного метода, n – общее число включенных в базис функций, aμi – коэффициенты, определяющие вклад базисной функции χi в собственную функцию ψμ.
Базисный набор определяет, насколько точно разложение аппроксимирует молекулярную орбиталь (МО), при этом число АО, аппроксимирующих МО с требуемой точностью, должно быть минимальным. Существует три основных критерия для выбора базисных функций.
1. Базисные функции должны давать в основном хорошее приближение к истинной волновой функции (например, возле ядер и на больших расстояниях от них).
2. Базисные функции должны допускать аналитическое вычисление нужных интегралов.
3. Полное число базисных функций не должно быть очень большим
На данный момент широко используются следующие наборы базисных функций:
· плоские волны 
;
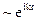· слэтеровские орбитали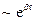 
;
· гауссовы орбитали 
;
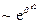· численные орбитали, форма которых оптимизируется из атомных расчетов.
Разложение по плоским волнам описывает обычно с хорошей точностью расчет электронной структуры периодичной кристаллической структуры. Также это разложение может быть успешно применено для расчета аморфных тел или конечных систем, таких как атомные кластеры или структуры с дефектами.
Слэтеровские орбитали являются наиболее естественными, если расчет начинается с изолированных атомов, так как функции слэтеровского типа являются точным решением водородоподобного атома. Однако некоторые интегралы кулоновского типа не могут быть решены аналитически при использовании этого набора. Квантово-химические расчеты с использованием слэтеровских функций в качестве базисных орбиталей являются достаточно сложными и трудоемкими.
В 1950 году С.Ф. Бойс предложил использовать базисные функции гауссова типа. Основное отличие от слэтеровских функций заключается в квадратичной зависимости от r аргумента экспоненты. Это позволяет представлять произведения гауссовых функций (центрированных в разных точках), встречающиеся в многоцентровых интегралах, в виде линейной комбинации одиночных гауссовых функций, центрированных в общем случае в другой точке пространства. В результате сильно упрощаются вычисления всех интегралов.
Проведение тестовых расчетов с использованием этих базисных наборов показало, что при n≥3 результаты расчетов очень схожи. Поэтому наиболее широкое распространение получил минимальный базисный набор STO-3G. Минимальные базисные наборы включают только атомные орбитали, которые необходимы для размещения электронов нейтрального атома.
В валентно-расщепленных базисных наборах валентные орбитали разделены на компактную и диффузную составляющие. Поэтому схема записывается как (m-npG), где m - число гауссовых функций, заменяющих каждую внутреннюю АО, n и p - число гауссовых функций с разными значениями экспонент, аппроксимирующих каждую валентную АО.
Для улучшения описания молекулярных орбиталей на больших расстояниях от ядра часто используют базисные наборы с включением поляризационных функций. Поляризационные функции - дополнительные волновые функции с l+1, где l - орбитальное квантовое число последних заполненных атомных орбиталей. Одними из наиболее используемых поляризационных базисных наборов являются 6-31G* и 6-31G**, где звездочка обозначает добавление поляризационных d- функций к p -элементам (или f -функций к d -элементам). Вторая звездочка обозначает добавление поляризационных p -функций к 1s -орбиталям атомов водорода.
Выбор базиса, подходящего для решения задачи, определяется стремлением получить более точное решение, с одной стороны, и ограничениями, связанными с ресурсами ЭВМ, с другой. Поэтому на практике применяется часто схема, когда полная оптимизация выполняется с использованием небольших базисов, после чего в более широких базисах проводятся расчеты для одной геометрической конфигурации и устанавливаются поправки, связанные с учетом электронной корреляции.
Практическая часть
