При численном решении уравнения Шредингера систем с большим числом частиц возникают сложности, связанные с невозможностью вычисления волновой функции с достаточной точностью и записью волновой функции в цифровом виде в память компьютера. Данные проблемы не могут быть решены посредством увеличения точности расчета или расширения памяти, так как в их основе лежит экспоненциальный рост ошибок или памяти. Путь решения проблемы был найден в работах Вальтера Кона с сотрудниками, отмеченных Нобелевской премией по химии 1998г, за разработку метода теории функционала плотности.
Теория функционала плотности (англ. density functional theory, DFT) является одним из наиболее широко используемых и универсальных методов в вычислительной физике и вычислительной химии. В основе метода лежат теоремы Хоэнберга—Кона.
1. Первая теорема утверждает, что существует взаимно однозначное соответствие между плотностью основного состояния электронной подсистемы, находящейся во внешнем потенциале атомных ядер, и самим потенциалом ядер.
2. Вторая теорема представляет собой вариационный принцип квантовой механики, сформулированный для функционала плотности и утверждает, что энергия электронной подсистемы, записанная как функционал электронной плотности, имеет минимум, равный энергии основного состояния.
Основная цель метода теории функционала плотности- заменить многоэлектронную волновую функцию при описании электронной подсистемы электронной плотностью. Это ведет к существенному упрощению задачи, поскольку многоэлектронная волновая функция зависит от переменных - по 3 пространственных координаты на каждый из электронов, в то время как плотность — функция лишь трёх пространственных координат.
Полную энергию для системы взаимодействующих электронов можно записать в виде:
(2.5)
Где Т представляет собой кинетическую энергию, второе слагаемое обеспечивает электростатическое отталкивание электронов. Vext - потенциал взаимодействия электрона с ядрами, а Exс - обменная корреляционная энергия. Вариационное решение этой задачи позволяет получить систему одночастичных уравнений Шредингера вида:
(2.6)
Где t - представляет собой кинетическую энергию отдельного электрона и
(2.7)
Где Vxc( r ) - обменно-корреляционный потенциал, включающий все многочастичные взаимодействия.
Основная проблема, связанная с методом теории функционала плотности заключается в том, что точные аналитические выражения для функционалов обменной и корреляционной энергии известны только для частного случая газа свободных электронов. В физических приложениях наиболее распространено приближение локальной плотности, в котором принято, что функционал, вычисляемый для некоторой точки пространства, зависит только от плотности в этой точке:
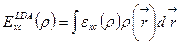(2.8)
εxc(ρ) в точке r зависит только от электронной плотности в данной точке ρ( r ). Обменная составляющая обменно-корреляционной энергии в приближении LDA определяется формулой Дирака
,
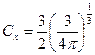
Приближение локальной спиновой плотности является непосредственным обобщением приближения локальной плотности, учитывающим спин электрона. Если плотности электронов с разной ориентацией спина α и β не равны, то обменная энергия в приближении LSDA вычисляется по формуле:
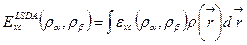(2.9)
Метод обобщённого градиентного приближения (GGA) также является локальным, но, в отличие от метода локальной плотности, учитывает градиент плотности в точке рассмотрения:
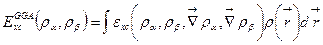(2.10)
Использование этого приближения дает хорошие результаты при расчете геометрии и энергии основного состояния молекул. Существуют и более точные приближения, которые в значительной степени позволяют решить проблему вычисления функционала обменно-корреляционной энергии.
В расчётах квантовой химии одним из распространённых является вид обменного функционала, называемый BLYP (Becke, Lee, Yang, Parr). Еще более широко распространено приближение B3LYP, которое основано на гибридном функционале, в котором обменная энергия рассчитывается с привлечением точного результата, полученного методом Хартри — Фока.
