Решение в программе Mathcad

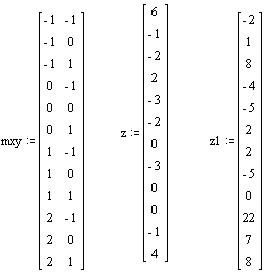
Пусть задан массив mxy, первый столбец которого содержит значения аргумента x, а второй – значения аргумента y. Таким образом, каждая строка этого массива есть координата точки в плоскости (x,y). Пусть также задан вектор соответствующих значений z. Чтобы получить уравнение полиноминальной регрессии k -той степени, применим функцию regress(mxy, z, k) (см. пример). В результате получим вектор коэффициентов искомой регрессии. Первые два элемента этого вектора игнорируем, третий элемент равен порядку полинома, т.е. k, остальные – искомые коэффициенты уравнения, расположенные в следующем порядке: сначала при одночленах xy^k-1, y^k, y^k-1, затем при y^k-2, xy^k-2, x²y^k-2;

y^k-3, xy^k-3, x²y^k-3, x³y^k-3;

y^k-4, xy^k-4, x²y^k-4, x³y^k-4, x⁴y^k-4;

……………………………….

y, xy, x²y,x³y, …, x^k-1y;

1, x, x², x³, …, x^k-1, x^k.

 

Таким образом, в примере, приведенном ниже, получены уравнения множественной полиноминальной регрессии второго порядка

z(x,y)=2xy+3y²-2y-3-x+x²

и третьего порядка z₁(x,y)=2xy²+1.5y³+4y²+1.5y-3xy-x²y-5-4x+3x²+x³.

 

 

СОДЕРЖАНИЕ ОТЧЕТА

 

 

1. Краткое описание методов, применяемых при выполнении задания.

2. Описание порядка выполнения задания.

3. Анализ полученных результатов.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сущность метода наименьших квадратов. Порядок нахождения коэффициентов уравнения регрессии.

2. Виды уравнений регрессии.

3. Оценка тесноты связи между переменными x и y.

4. Линеаризация уравнений регрессии.

5. Получение уравнений различных видов регрессии. Порядок действий в Excel.

6. Получение дополнительной регрессионной статистики. Порядок действий в Excel.

7. Получение уравнения регрессии произвольного вида. Порядок действий в Excel.

8. Линейная интерполяция в Mathcad.

9. Полиноминальная интерполяция в Mathcad.

10. Получение уравнения множественной линейной регрессии в Excel и в Mathcad.

 

 

ВАРИАНТЫ ЗАДАНИЙ

 

Исходные данные для заданий 1-5.

 

1.

x		1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9
y	0,686	0,742	0,767	0,646	0,807	0,774	0,97	0,932	0,936	0,978	1,048

 

2.

x		2,1	2,2	2,3	2,4	2,5	2,6	2,7	2,8	2,9
y	2,312	2,251	2,418	2,752	2,459	2,7	3,022	3,079	2,42	2,669	3,241

 

3.

x		3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9
y	4,615	4,591	5,13	5,481	5,492	5,553	5,471	5,727	5,798	6,11	6,605

 

4.

x		4,1	4,2	4,3	4,4	4,5	4,6	4,7	4,8	4,9
y	8,472	8,805	9,096	8,993	9,312	9,465	9,771	9,61	9,722	11,419	10,285

 

5.

x		5,1	5,2	5,3	5,4	5,5	5,6	5,7	5,8	5,9
y	12,36	13,63	13,304	13,148	13,482	14,24	14,516	14,882	15,246	15,369	15,158

 

6.

x		6,1	6,2	6,3	6,4	6,5	6,6	6,7	6,8	6,9
y	17,631	19,747	19,783	18,806	19,886	21,118	20,208	19,481	20,153	20,505	21,29

7.

x		7,1	7,2	7,3	7,4	7,5	7,6	7,7	7,8	7,9
y	25,243	25,133	25,669	26,627	26,753	27,234	26,491	26,876	27,228	28,065	27,781

 

8.

x		8,1	8,2	8,3	8,4	8,5	8,6	8,7	8,8	8,9
y	30,528	34,221	34,233	34,114	33,595	34,058	34,498	35,822	35,678	37,442	35,698

 

9.

x		9,1	9,2	9,3	9,4	9,5	9,6	9,7	9,8	9,9
y	41,742	42,244	43,884	42,167	43,696	45,042	42,461	45,727	44,056	45,863	44,953

 

10.

x		10,1	10,2	10,3	10,4	10,5	10,6	10,7	10,8	10,9
y	49,758	51,954	50,083	52,376	53,413	54,966	52,771	54,115	55,476	55,688	56,196

 

11.

x		11,1	11,2	11,3	11,4	11,5	11,6	11,7	11,8	11,9
y	62,173	63,055	63,725	64,237	64,086	63,587	65,412	65,284	65,05	68,876	65,74

 

12.

x		12,1	12,2	12,3	12,4	12,5	12,6	12,7	12,8	12,9
y	71,167	74,264	72,658	74,507	76,649	75,517	75,708	76,359	79,316	77,373	77,698

 

13.

x		13,1	13,2	13,3	13,4	13,5	13,6	13,7	13,8	13,9
y	86,612	85,491	87,803	88,613	89,075	89,24	89,633	90,761	91,323	91,428	91,712

 

x		14,1	14,2	14,3	14,4	14,5	14,6	14,7	14,8	14,9
y	99,811	100,31	99,492	102,61	103,20	104,36	104,73	105,16	104,65	105,58

 

15.

x		15,1	15,2	15,3	15,4	15,5	15,6	15,7	15,8	15,9
y	115,18	115,28	115,18	116,01	117,20	119,04	121,43	119,35	120,84	121,58	124,33

 

16.

x		16,1	16,2	16,3	16,4	16,5	16,6	16,7	16,8	16,9
y	131,96	126,72	132,26	131,29	132,04	133,74	133,28	135,75	134,6	139,84	133,23

 

17.

x		17,1	17,2	17,3	17,4	17,5	17,6	17,7	17,8	17,9
y	147,67	150,75	149,74	150,74	147,94	147,77	152,08	154,65	154,98	152,55

 

18.

x		18,1	18,2	18,3	18,4	18,5	18,6	18,7	18,8	18,9
y	164,69	163,25	164,47	165,50	166,77	167,46	169,65	169,42	170,50	174,22	173,14

 

19.

x		19,1	19,2	19,3	19,4	19,5	19,6	19,7	19,8	19,9
y	186,36	180,38	184,45	186,04	189,29	188,32	184,83	186,44	194,55	192,34	191,89

 

20.

x		20,1	20,2	20,3	20,4	20,5	20,6	20,7	20,8	20,9
y	200,30	200,96	200,73	202,89	208,23	208,89	209,51	206,87	209,17	214,21

 

Исходные данные для задания 6 подберите самостоятельно. Рекомендуется выбрать 20 пар значений (x, y) и соответствующие им значения z.

 

 

ТЕХНИКА БЕЗОПАСНОСТИ

ПРИ ВЫПОЛНЕНИИ ЛАБОРАТОРНОЙ РАБОТЫ

 

Разрешение на выполнение лабораторной работы дает руководитель лабораторного практикума после проверки знаний техники безопасности и готовности группы к выполнению лабораторной работы.

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторной работе № 6 по математике

 

 

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

 

ЦЕЛЬ РАБОТЫ: На основе выборочных данных получить статистические числовые характеристики, с их помощью оценить параметры генеральной совокупности, изучить статистический закон распределения.

 

 

ЗАДАНИЕ

1. Составить статистический интервальный ряд частот и относительных частот так, чтобы . Построить гистограмму относительных частот.

2. Найти эмпирическую функцию распределения, эмпирическую плотность распределения.

3. Найти несмещенные точечные оценки математического ожидания и дисперсии генеральной совокупности.

4. Считая, что генеральная совокупность распределена по нормальному закону, найти доверительные интервалы для математического ожидания и среднеквадратического отклонения с надежностью 0,95; 0,99; 0,999. Сравнить полученные результаты.

5. Проверить гипотезу s(X)=s(Y).Согласуясь с полученным результатом, проверить гипотезу M(X)=M(Y).

6. Проверить, относятся ли две заданные выборки к одной и той же генеральной совокупности.

7. По первой из двух заданных выборок проверить гипотезу о нормальном распределении с.в. Построить многоугольники распределения эмпирических и теоретических частот.

8. В вариантах 1, 4, 7, 10, 13, 16, 19 по второй из двух заданных совокупностей проверить гипотезу о показательном распределении генеральной совокупности, в вариантах 2, 5, 8, 11, 14, 17, 20 – о распределении по биноминальному закону, в вариантах 3, 6, 9, 12, 15, 18 – о распределении по равномерному закону. Построить многоугольники распределения эмпирических и теоретических частот.

9. Составить уравнение линейной регрессии y на x. Проверить значимость коэффициента регрессии.

 

 

ВАРИАНТЫ ЗАДАНИЙ

Выполнить задания 1-8.

 

Вариант 1.

14; 11; 13; 12; 10; 17; 15; 9; 7; 6; 9; 15; 14; 15; 17; 19; 9; 6; 16; 14; 7; 17; 14; 15; 11; 12; 9; 17; 14; 16; 17; 8; 5; 17; 13; 18; 16; 14; 15; 17; 16; 18; 19; 15; 14; 16; 18; 16; 14; 15.

 

14; 13; 18; 15; 12; 13; 14; 12; 13; 16; 15; 15; 12; 13; 15; 14; 16; 18; 13; 15; 14; 16; 14; 13; 15; 12; 18; 12; 14; 16; 12; 13; 15; 15; 15; 13; 14; 15; 18; 16; 12; 15; 13; 13; 13; 15; 15; 17; 17.

 

Вариант 2.

11; 15; 20; 25; 29; 34; 19; 25; 16; 21; 29; 20; 28; 35; 21; 22; 23; 26; 28; 30; 18; 13; 17; 22; 29; 26; 33; 36; 39; 14; 16; 24; 27; 25; 31; 32; 23; 37; 23; 27; 34; 37; 36; 42; 32; 34; 39; 38; 44.

 

16; 13; 11; 15; 18; 19; 21; 18; 17; 15; 13; 16; 18; 17; 19; 15; 13; 12; 14; 16; 17; 20; 17; 17; 20; 19; 18; 22; 24; 18; 15; 14; 10; 12; 16; 18; 18; 19; 21; 23; 20; 22; 24; 17; 16; 14; 15; 18; 15; 11; 16; 17; 15; 13; 16; 17; 18; 14; 15; 19; 17; 18; 16; 13; 15; 17; 21; 23; 26; 19; 22; 24; 25; 20; 21; 24; 19; 22; 23; 20; 25; 21; 20; 22; 26; 19; 22; 23; 25; 28; 20; 21; 27; 19.

 

Вариант 3

 

0,90; 0,79; 0,84; 0,86; 0,88; 0,90; 0,92; 0,89; 0,85; 0,91; 0,98; 0,91; 0,80; 0,87; 0,89; 0,88; 0,78; 0,84; 0,81; 0,85; 0,88; 0,94; 0,86; 0,80; 0,86; 0,91; 0,91; 0,78; 0,86; 0,91; 0,95; 0,97; 0,88; 0,79; 0,82; 0,84; 0,90; 0,81; 0,87; 0,91; 0,90; 0,82; 0,85; 0,90; 0,96; 0,98; 0,89; 0,87; 0,99; 0,85.

 

0,90; 0,88; 0,19; 0,89; 0,93; 0,96; 0,98; 0,96; 0,90; 0,92; 0,93; 0,91; 0,86; 0,92; 0,91; 0,94; 0,90; 0,88; 0,90; 0,93; 0,95; 0,99; 0,91; 0,34; 1,00; 0,83; 0,93; 0,95; 0,96; 0,91; 0,89; 0,97; 0,90; 0,93; 0,95; 1,00; 0,83; 0,85; 0,87; 0,90; 0,92; 0,88; 0,97; 0,91; 0,92; 0,89; 0,99; 0,90; 0,94.

 

Вариант 4

 

30; 19; 21; 23; 26; 27; 29; 31; 24; 25; 28; 28; 27; 23; 26; 32; 34; 26; 24; 22; 19; 23; 27; 30; 29; 25; 18; 18; 5; 20; 22; 24; 28; 31; 33; 25; 18; 21; 26; 30; 32; 34; 29; 28; 21; 20; 23; 25; 27; 30; 32.

 

17; 27; 12; 28; 32; 39; 50; 57; 68; 78; 82; 13; 23; 47; 80; 28; 37; 22; 18; 12; 33; 48; 58; 71; 12; 26; 85; 30; 42; 44; 19; 13; 31; 34; 55; 72; 14; 25; 46; 52; 65; 14; 15; 24; 85; 45; 54; 62; 56; 53.

 

 

Вариант 5

160; 210; 260; 285; 310; 330; 85; 190; 230; 290; 305; 325; 351; 405; 247; 265; 308; 345; 360; 410; 130; 165; 170; 240; 272; 292; 348; 370; 200; 225; 280; 340; 390; 180; 190; 232; 250; 253; 263; 380; 420; 340; 325; 310; 400; 240; 220; 290; 350; 333; 405; 295; 450; 285; 225; 300; 355; 310; 385; 348; 245; 350; 335; 392; 381.

 

261; 260; 258; 263; 257; 260; 264; 259; 261; 260; 264; 261; 265; 261; 660; 263; 260; 260; 259; 260; 258; 265; 259; 265; 261; 258; 259; 259; 259; 259; 262; 264; 258; 259; 263; 266; 259; 261; 266; 262; 259; 262; 261; 259; 262; 262; 261; 266; 259; 262.

 

Вариант 6

 

50; 52; 140; 138; 165; 162; 210; 165; 170; 142; 150; 170; 168; 163; 63; 68; 88; 85; 105; 110; 112; 131; 125; 126; 135; 148; 92; 99; 102; 110; 115; 118; 125; 121; 118; 130; 133; 141; 182; 199; 205; 127; 132; 135; 98; 105; 119; 115; 125; 124.

 

85; 76; 80; 84; 88; 89; 91; 88; 84; 85; 75; 82; 86; 89; 88; 84; 90; 89; 85; 91; 87; 81; 78; 85; 88; 91; 89; 87; 74; 81; 87; 90; 88; 86; 76; 84; 88; 77; 82; 85; 84; 74; 80; 84; 91; 93; 90; 88; 87; 77; 83; 89; 89; 91; 92; 88; 94; 90; 88; 81; 83; 89; 94; 96; 88; 95; 99; 90; 86; 78; 81; 86; 90; 92; 93; 90; 83; 79; 86; 90; 79; 82; 87; 85; 91; 97; 88; 85; 87; 90; 89; 95; 89; 84; 91; 89; 90; 98; 91; 88.

 

Вариант 7

 

19,2; 18,1; 18,4; 18,2; 18,6; 18,9; 19,0; 19,7; 18,9; 19,2; 18,4; 18,5; 19,3; 18,3; 18,7; 18,8; 19,1; 19,4; 19,7; 19,1; 18,9; 19,3; 18,4; 19,2; 18,2; 18,7; 19,5; 19,3; 18,5; 18,6; 18,8; 19,1; 18,7; 19,1; 19,6; 18,6; 18,8; 19,1; 19,0; 19,5; 19,3; 18,8; 19,0; 19,5; 18,9; 19,0; 19,8; 19,8; 19,9.

 

19,5; 19,5; 19,6; 19,8; 20,0; 20,2; 20,4; 19,6; 19,9; 19,9; 20,0; 20,3; 20,2; 19,6; 20,1; 20,3; 20,5; 20,4; 19,8; 19,7; 19,8; 20,0; 20,1; 19,7; 20,3; 20,2; 20,1; 20,3; 20,2; 20,1; 24,4; 20,5; 20,3; 20,5; 20,2; 20,5; 20,7; 21,0; 20,4; 20,3; 20,2; 20,4; 20,6; 21,0; 20,6; 20,7; 20,8; 20,7; 20,8; 21,1.

 

Вариант 8

 

48; 29; 6; 18; 24; 30; 35; 25; 17; 23; 27; 33; 28; 19; 14; 8; 24; 36; 42; 47; 40; 28; 12; 7; 25; 27; 15; 6; 16; 25; 34; 40; 27; 20; 6; 13; 28; 37; 43; 27; 38; 53; 24; 41; 21; 11; 17; 25; 46; 51.

 

18; 20; 31; 45; 52; 60; 35; 15; 21; 33; 47; 55; 62; 36; 40; 49; 56; 61; 54; 30; 15; 22; 32; 44; 63; 41; 52; 17; 21; 30; 54; 65; 51; 42; 26; 32; 45; 50; 64; 25; 39; 42; 42; 53; 69; 58; 45; 29; 34; 46; 59; 37; 20; 43; 55; 5; 52; 38; 48; 51.

 

 

Вариант 9

 

95; 57; 15; 26; 35; 46; 52; 55; 59; 47; 36; 31; 13; 17; 32; 42; 48; 58; 56; 102; 96; 45; 54; 56; 60; 64; 55; 53; 37; 30; 10; 16; 20; 49; 48; 43; 12; 19; 51; 103; 97; 28; 11; 27; 51; 62; 61; 38; 29; 10; 39; 40; 18; 14; 41; 50; 57; 61; 71; 73; 58; 63; 59; 60; 63; 68; 70; 71; 75; 82; 76; 85; 90; 83; 86; 87; 92; 99; 66; 68; 78; 91; 94; 77; 65; 72; 69; 76; 84; 98; 79; 67; 74; 80; 89; 69; 81; 88; 100; 90.

 

40; 62; 82; 100; 110; 119; 91; 32; 47; 80; 95; 39; 90; 102; 116; 105; 102; 118; 120; 140; 159; 117; 122; 135; 43; 59; 63; 85; 101; 170; 30; 45; 75; 87; 37; 50; 90; 104; 119; 101; 31; 51; 54; 70; 88; 96; 106; 112; 139; 130.

 

Вариант 10

 

3; 4; 8; 12; 14; 19; 18; 23; 2; 3; 5; 9; 12; 10; 13; 6; 10; 10; 7; 11; 15; 6; 12; 10; 14; 16; 5; 11; 11; 10; 13; 10; 8; 11; 7; 9; 12; 9; 14; 13; 16; 18; 11; 10; 12; 9; 9; 15; 13; 11; 12.

 

3; 5; 6; 5; 6; 4; 5; 6; 4; 5; 5; 6; 1; 2; 4; 5; 6; 4; 5; 4; 6; 5; 6; 5; 6; 2; 4; 5; 4; 5; 5; 3; 6; 1; 3; 4; 5; 4; 5; 4; 7; 6; 5; 6; 4; 5; 2; 5; 4; 5; 5; 6; 3; 5; 2; 4; 5; 4; 5; 4; 7; 6; 6; 3; 6; 5; 7; 5; 4; 5; 5; 7; 9; 10; 9; 7; 8; 4; 7; 4; 10; 9; 5; 8; 4; 8; 7; 8; 4; 5; 5; 9; 10; 8; 5; 8; 5; 4; 5; 7.

 

Вариант 11

 

4,7; 7,2; 6,2; 6,7; 7,2; 5,7; 5,2; 7,7; 8,2; 6,2; 7,2; 5,7; 6,2; 5,7; 8,2; 5,7; 6,7; 6,2; 5,7; 6,2; 6,7; 5,2; 7,7; 6,2; 7,2; 6,7; 7,7; 6,2; 7,2; 8,2; 6,2; 5,7; 6,2; 6,7; 7,2; 5,7; 6,7; 7,7; 8,2; 4,7; 8,7; 4,2; 4,7; 8,7; 6,2; 6,7.

 

3; 7; 8; 3; 7; 7; 6; 7; 6; 7; 5; 8; 2; 10; 5; 8; 7; 6; 7; 6; 7; 6; 7; 8; 5; 11; 5; 7; 8; 7; 4; 5; 2; 3; 8; 5; 7; 6; 7; 10; 7; 8; 7; 8; 4; 7; 5; 7; 6; 11; 10; 5; 6; 3; 5; 7; 8; 7; 8; 6; 7; 4; 9; 10; 8; 4; 8; 9; 6; 7; 10; 7; 7; 7; 9; 7; 6; 8; 9; 6; 4; 7; 4; 6; 11; 9; 5; 9; 6; 7; 6; 7; 6; 7; 4; 6; 7; 6; 7; 11.

 

Вариант 12

 

1,03; 1,06; 1,09; 1,12; 1,01; 1,06; 1,05; 1,10; 1,09; 1,13; 1,20; 1,04; 1,08; 1,10; 1,15; 1,11; 1,02; 1,04; 1,04; 1,07; 1,11; 1,14; 1,05; 1,07; 1,10; 1,13; 1,14; 1,08; 1,06; 1,08; 1,09; 1,13; 1,12; 1,16; 1,09; 1,17; 1,10; 1,15; 1,11; 1,13; 1,10; 1,14; 1,19; 1,21; 1,11; 1,18; 1,23; 1,10; 1,19; 1,03.

 

1,47; 1,54; 1,56; 1,57; 1,59; 1,60; 1,87; 1,64; 1,83; 1,76; 1,72; 1,74; 1,61; 1,77; 1,68; 1,73; 1,71; 1,74; 1,61; 1,84; 1,60; 1,77; 1,61; 1,71; 1,78; 1,62; 1,78; 1,64; 1,72; 1,63; 1,74; 1,72; 1,71; 1,68; 1,72; 1,74; 1,64; 1,66; 1,72; 1,63; 1,66; 1,74; 1,73; 1,62; 1,67; 1,62; 1,61; 1,72; 1,67; 1,71.

 

Вариант 13

 

5,12; 4,44; 4,54; 4,32; 4,45; 4,56; 4,69; 4,60; 4,53; 4,46; 4,37; 4,28; 4,47; 4,48; 4,38; 4,30; 4,49; 4,55; 4,68; 4,91; 5,10; 4,55; 4,57; 4,70; 4,81; 5,02; 5,04; 4,82; 4,75; 4,59; 4,53; 4,60; 4,74; 4,49; 4,61; 4,79; 4,90; 5,05; 5,07; 5,12; 5,08; 4,31; 4,52; 4,46; 4,63; 4,51; 4,34; 4,26; 4,50; 4,62; 4,73; 4,77; 4,49; 4,36; 4,29; 4,42; 4,50; 4,78; 4,52; 4,93; 4,82; 5,12; 4,27; 4,33; 4,54; 4,64; 4,71; 4,69; 4,80.

 

4,21; 5,19; 4,38; 4,96; 5,07; 4,56; 4,25; 5,00; 4,85; 5,15; 4,79; 4,38; 5,12; 5,15; 4,62; 4,53; 4,28; 5,00; 4,86; 4,99; 5,03; 5,14; 4,66; 4,46; 5,13; 4,78; 4,99; 5,02; 5,12; 5,19; 4,96; 4,57; 4,20; 5,20; 4,65; 4,81; 5,17; 4,31; 4,88; 5,00.

 

Вариант 14

 

-5; 0; 3; -3; -1; 1; -5; 4; -4; -2; -2; 2; 4; 0; -4; -5; -2; -3; -2; 4; -3; 1; 2; 3; -5; -4; 3; -2; -1; -3; -5; -3; 3; 0; 2; 1; -1; -4; -2; 2; 0; -2; 2; -4; -3; 3; -3; 2; -3; -2; -4; -3; -1; 1; -3; -2; -3; -4; -3; -2; -2; -1; -3; -2; -1; -2; -3; -2; -3; -1; -2; -1; -2; -3; -2; -1; -2; -3; -1; -2; -2; -1; -3; -2; -1; -2; -1; -2; -3; -2; -2; -3; -2; -1; -2; 1; 0; 2; 1; 2.

 

-4; 0; -1; 0; -2; 0; -1; 0; 1; -3; -1; 0; -2; 0; -1; 0; 1; -2; 0; 1; -2; -1; 0; -1; 4; 1; -2; 4; 1; -3; -1; 0; -4; 0; -2; -1; -4; 0; -2; 0; -2; -3; 0; 3; -2; 0; -1; 1; 3; -3; 0; -2; -1; 0; -4; -2; 1; -2; 2; 0; 1; 0; -2; 1; 1; 2; 0; 2; -4; -3; -1; -4; 0; -2; 0; -1; 0; 0; -1; 0; -3; -1; 0; -1; 5; 0; -3; -1; 0; -1; -3; -1; 0; -2; -1; 0; -1.

 

Вариант 15

 

-2; 1; -1; 0; 1; 3; 4; 7; 4; 7; 3; 2; 3; 2; 3; 2; 3; 2; 3; 2; 3; 2; 1; 0; 1; 0; 4; 7; 4; 6; 1; 0; 1; -2; 1; 2; 4; 2; 7; 6; 1; -1; 1; 0; 1; 0; 1; -1; 1; 5; 0; 1; 2; 6; 1; -1; 4; 1; 0; 6; 6; 1; -1; 1; -2; 0; 1; 5; 6; 5; 0; 2; 1; 0; 5; 1; -1; 5; 1; 2; 1; 6; 5; 2; 1; 0; 1; 2; 1; -1; 1; 0; 1; 2; 1; 0; 1; -1; 1; 2.

 

-2; 3; 1; 0; 1; 3; 1; 1; 3; 0; 2; -1; 2; 1; 2; -1; 2; 0; 2; 1; 0; 1; 3; -3; 1; 1; 2; 1; 3; 0; 1; -2; 0; 1; 1; 3; 0; 1; 2; 1; 2; 1; 1; 2; -1; 2; -1; -3; 3; -2; 0; 3; -1; 2; 3; 1; 0; 3; 2;1; 2; 1; -2; 4; 1; 4; 1; 4; 6; 0; 1; 4; 0; 2; 0; -3; -1; 0; 4; 1; 0; -1; 5; 1; 0; 2; 1; 5; 6; 6; 2; 5; 0; 5; 1; 5; -1; 0; 6; 0.

 

Вариант 16

 

1; 3; 2; 3; 2; 3; 3; 2; 3; 2; 3; 2; 1; 3; 3; 2; 6; 7; 3; 6; 3; 4; 2; 0; 1; 2; 3; 2; 3; 6; 3; 2; 4; 3; 4; 0; 1; 3; 8; 3; 3; 7; 3; 2; 4; 3; 4; 3; 5; 2; 3; 2; 3; 7; 3; 1; 2; 4; 5; 6; 1; 3; 2; 2; 4; 2; 3; 7; 3; 2; 2; 6; 3; 4; 3; 0; 3; 2; 4; 3; 3; 2; 8; 2; 3; 4; 3; 1; 2; 5; 2; 3; 5; 4; 3; 1; 4; 2; 5; 2.

 

3; 4; 3; 4; 3; 4; 3; 4; 3; 4; 2; 4; 2; 7; 5; 2; 5; 7; 4; 3; 4; 5; 7; 5; 6; 4; 6; 5; 6; 4; 3; 2; 3; 0; 4; 5; 2; 4; 4; 3; 4; 5; 4; 5; 2; 4; 5; 6; 5; 4; 5; 3; 5; 1; 7; 1; 7; 2; 6; 3; 3; 2; 3; 8; 3; 8; 4; 5; 3; 4; 4; 3; 4; 2; 4; 1; 4; 2; 9; 3; 3; 4; 3; 4; 3; 4; 8; 4; 9; 4; 4; 3; 4; 3; 4; 1; 4; 8; 4; 3.

 

 

Вариант 17

 

5; 8; 7; 9; 8; 8; 9; 5; 9; 12; 8; 9; 5; 8; 9; 12; 8; 5; 9; 5; 9; 12; 7; 8; 4;9; 5;8; 5; 8; 9; 4; 9; 7; 8; 4; 8; 13; 9; 13; 9; 7; 9; 2; 7; 3; 8; 8; 8; 12; 8; 5; 3; 13; 9; 10; 3; 8; 7; 9; 10; 7; 8; 5; 8; 7; 13; 7;8; 5; 8; 9; 7; 8; 9; 8; 13; 8; 10; 8; 9; 7; 9; 7; 8; 7; 10; 7; 8; 12; 7; 10; 7; 10; 7; 8; 8; 5; 9; 8.

 

5; 4; 5; 4; 5; 4; 5; 4; 5; 4; 4; 6; 4; 6; 4; 6; 4; 6; 4; 6; 5; 4; 6; 4; 5; 4; 6; 4; 5; 4; 4; 6; 4; 3; 4; 5; 4; 3; 5; 4; 5; 4; 5; 4; 5; 4; 5; 4; 2; 6; 5; 2; 5; 3; 5; 6; 5; 3; 6; 7; 6; 6; 5; 7; 6; 4; 5; 2; 6; 2; 5; 2; 6; 7; 6; 2; 6; 5; 6; 5; 10; 5; 7; 5; 7; 4; 11; 6; 5; 6; 5; 9; 5; 9; 5; 2.

 

Вариант 18

 

2; -1; -4; 5; 2; 0; 2; 0; 6; 2; 5; 7; 2; -1; 0; 4; -3; 2; 6; 4; 2; 5; 7; -4; 2; -1; 4; 2; 4; 2; 5; -3; 2; 5; 0; 2; 0; 6; 6; 0; 2; -1; 5; 7; 7; -4; 6; 2; 4; 2; 5; 5; 2; -3; 0; 4; 0; 4; 6; 0; 2; 7;

-1; 0; 4; -3; 4; 6; 4; 2; 5; 2; 5; 2; 7; 4; 6; 4; 6; 0; 2; 7; 4; 7; 4; 8; -3; 8; 4; 2; 8; 2; 8; 2; 8; 5; 8; 2; 8; 0.

 

0; 3; 4; 2; 4; 2; 3; 2; 3; 2; 3; 6; -2; 3; 4; 3; 4; 3; 4; 3; 0; 3; 6; 2; 3; 2; 4; 2; 3; 2; 4; 3; 4; 3; -2; 4; 4; 3; 4; 3; 0; -1; 2; 4; 3; 6; -1; 6; 3; 2; 4; 6; 4; -1; 4; 3; 4; 3; 4; 3; 0; 4; 6; 2; 6; -1; 3; 4; 3; 2; 7; 6; 4; 6; 2; 4; 2; 6; 2; 3; 0; 7; 8; 8; 8; 7; 6; 3; 9; 2; 7; 0; 7; 0; 7; 3; 6; 3; 6; 3.

 

Вариант 19

 

3; 4; 3; 8; 3; 8; 3; 4; 8; 4; 4; 3; -4; 2; 3; 2; 4; 3; 2; 3; 2; 8; 4; 8; 0; 4; 0; 2; 3; 2; 3; 3; 2; -4; 6; -2; 6; 3; 6; 3; 4; 6; 0; 6; 2; 11; 0; 2; 0; 2; 3; 0; 6; 3; 10; -4; 4; 0; 3; 2; 10; 6; 3; -2; 0; 3; 8; -2; 2; 3; 3; -2; 11; 2; 2; 3; -2; 2; 4; 3; 0; 2; 3; 10; -2; 6; 2; -2; 8; -2; 3; 10; 2; 3; 2; 3; 10; 3; 2; 3; 2.

 

5; 6; 5; 6; 5; 7; 5; 9; 7; 1; 6; 10; 6; -1; 7; 5; 3; 6; 5; 6; -3; 6; 5; 7; 5; 6; 8; 3; 7; 5; 7; 5; 6; 8; 3; 7; 5; 7; 5; 7; -1; 6; 3; 6; 6; 6; 1; 7; 6; -3; 7; 6; -1; 7; 3; 1; 7; 5; 7; 6; -1; 7; 8; 3; 6; 7; 6; -3; 6; 5; 6; 3; 7; 6; 6; 1; 7; 5; 3; 7; 3; 7; -1; 7; 3; 7; 5; 7; 5; 6; -3; 6; 7; 6; 6; 1; 7; 1; 7; 1; 5; 7; 8; 8; 3.

 

Вариант 20

 

-1; 3; 0; 3; 5; 3; 5; 2; 5; 2; 2; 5; 3; 5; 0; 5; 2; 5; 3; 5; 5; 5; 12; -2; 12; 5; 0; 5; 5; 2; 2; -1; 5; -1; 5; 2; 5; 3; 0; 10; 0; 5; 0; 5; -2; 6; 0; 6; 2; 6; 5; 3; 3; 2; 5; -1; 5; 3; 6; 2; 0; 5; -1; 5; 3; -2; 6; 2; -1; 6; 8; 3; 5; 3; 5; 5; 3; 5; 3; 6; 0; 8; 3; 6; 3; 6; -1; 5; 6; 2; 8; 3; 8; 3; 8; 6; 10; 6; 10; 6.

 

5; -2; 3; 5; 9; 0; -2; 0; -1; 0; 0; 9; 9; 0; 2; -1; 9; -1; 0; -1; 9; 5; 6; -1; 2; -2; 2; -2; -1; 0; 0; 0; -1; 5; 0; -3; 0; -1; 9; -1; 7; -1; -5; 0; 3; 2; 0; -2; 0; -2; 1; 9; -1; 5; -5; 7; -3; 1;

-3; -1; 7; 1; -2; 5; 0; -2; 2; -1; 1; -2; 0; 3; -1; 1; 7; -3; 7; -3; 2; 3; 7; 0; -1; 3; 1; -1; 2; -1; 0; -2; 1; 3; 1; -1; 0; 0; 1; 2; 3; 7.

 

 

Выполнить задание

9.

Вариант 1

x
y					3.7	3.6	3.5			3.5

 

Вариант 2

x
y	6.9	8.7	6.4	8.4	6.1	9.4		6.4	9.3	8.2	8.6

 

Вариант 3

x

y

Вариант 4

x
y

 

Вариант 5

x
y

 

Вариант 6

x
y

 

Вариант 7

x
y

 

Вариант 8

x
y

 

Вариант 9

x
y

 

Вариант 10

x
y

 

Вариант 11

x

y

 

 

Вариант 12

x

y

 

Вариант 13

x	0.866	0.833	0.883	0.801	0.848	0.730	0.514	0.566	0.717	0.711
y

 

Вариант 14

x	0.446	0.393	0.328	0.445	0.513	0.626	0.589	0.672	0.711	0.717
y

 

Вариант 15

x	14.9	11.7	11.7	18.8	10.7	10.9	34.8	41.7	22.8	20.7
y

Вариант 16

x	36.7	41.6	41.3	46.8	17.3	17.5	22.5	17.7	20.7	22.8
y

 

Вариант 17

x

y

 

Вариант 18

x

y

 

Вариант 19

x	31.3	13.4	4.5	10.0	20.0	15.0	137.1	17.9	165.4	2.0	6.8	27.1
y	0.9	1.7	0.7	1.7	2.6	1.3	4.1	1.6	6.9	0.4	1.3	1.9

Вариант 20

x	18.9	13.7	18.5	4.8	21.8	5.8	99.0	20.1	60.6	1.4	8.0	18.9
y	0.9	1.7	0.7	1.7	2.6	1.3	4.1	1.6	6.9	0.4	1.3	1.9

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Пусть в результате некоторого опыта получена следующая выборка:

 

a. Составить статистический интервальный ряд частот и относительных частот так, чтобы . Построить гистограмму относительных частот.

b. Найти эмпирическую функцию распределения, эмпирическую плотность распределения.

c. Найти несмещенные точечные оценки математического ожидания и дисперсии генеральной совокупности.

d. Считая, что генеральная совокупность распределена по нормальному закону, найти доверительные интервалы для математического ожидания и среднеквадратического отклонения с надежностью 0,95; 0,99; 0,999. Сравнить полученные результаты.

e. Проверить гипотезу s(X)=s(Y).Согласуясь с полученным результатом, проверить гипотезу M(X)=M(Y).

f. Проверить, относятся ли две заданные выборки к одной и той же генеральной совокупности.

g. По первой из двух заданных выборок проверить гипотезу о нормальном распределении с.в. Построить многоугольники распределения эмпирических и теоретических частот.

h. В вариантах 1, 4, 7, 10, 13, 16, 19 по второй из двух заданных совокупностей проверить гипотезу о показательном распределении генеральной совокупности, в вариантах 2, 5, 8, 11, 14, 17, 20 – о распределении по биноминальному закону, в вариантах 3, 6, 9, 12, 15, 18 – о распределении по равномерному закону. Построить многоугольники распределения эмпирических и теоретических частот.

i. Составить уравнение линейной регрессии y на x. Проверить значимость коэффициента регрессии.

Решение в программе Excel

 

С помощью функции СЧЕТ в категории Статистические определим объем выборки. Определим наименьшую варианту (функция МИН) и наибольшую варианту (функция МАКС). Зная объем выборки n, определим число интервалов ряда так, чтобы в каждом интервале содержалось 8-12 вариант. Пусть в нашем случае в каждом интервале содержится 10 вариант. Тогда n=90, k=n/10=9 интервалов. Найдем шаг интервального ряда

h=(MAKC-МИН)/k=3.977778.

Сгруппируем ряд с помощью функции ЧАСТОТА (массив данных, массив карманов). Эта функция вводится как формула массива после выделения смежных ячеек под результат. Число этих ячеек равно числу интервалов, но на одну меньше, чем число ячеек в массиве карманов. Запишем интервалы (ai; bi). В процессе вычислений абсолютную ссылку на ячейку можно установить с помощью функциональной клавиши F4. Выделим ячейки под результат (здесь – ячейки в столбце ni). Выберем функцию ЧАСТОТА. Массив данных – элементы выборки, массив карманов – масссив элементов столбца bi с 156,9778 по 184,8222.

 

Далее вычислим относительные частоты wi и плотности относительных частот wi/h. Построим гистограмму относительных частот.

 

Гистограмма относительных частот является графиком эмпирической плотности распределения. Эмпирическую функцию распределения можно найти по определению.

Точечные оценки параметров распределения можно найти непосредственно или с помощью функций ДИСП (s²), КВАДРОТКЛ ( =nD_в), СТАНДОТКЛОН (s).

Доверительный интервал для среднего генеральной совокупности можно найти с помощью функции

ДОВЕРИТ(a, s, n), которая выдает точность оценки d, т.е. доверительный интервал имеет вид . Причем a - уровень значимости,g=1-a, s предполагается известным. Но т.к. s неизвестно, найдите доверительный интервал для a также и непосредственно. Сравните результаты. Найдите доверительный интервал для s.

 

При поверке гипотезы о равенстве дисперсий двух совокупностей можно применить функцию ФТЕСТ(массив 1, массив 2), которая выдает вероятность того, что дисперсии массивов 1 и 2 отличаются несущественно.

 

При проверке гипотезы о равенстве математических ожиданий двух совокупностей можно применить функцию ТТЕСТ (массив 1, массив 2, хвосты, тип), которая выдает вероятность того, что две выборки взяты из совокупностей, имеющих одно и то же среднее. Аргумент хвосты=1, если используется одностороннее распределение, т. е. в качестве конкурирующей гипотезы рассматривается гипотеза M(X)<M(Y) или M(X)>M(Y). Аргумент хвосты=2, если используется двустороннее распределение, т. е. в качестве конкурирующей гипотезы рассматривается гипотеза M(X)¹M(Y). Аргумент тип =1, если применяется парный тест, тип =2, если применяется двухвыборочный тип с равными дисперсиями (гомоскедастичный), тип =3, если применяется двухвыборочный тип с неравными дисперсиями (гетероскедастичный).

 

При проверке гипотезы о законе распределения генеральной совокупности можно применять функцию ХИ2ТЕСТ (фактический интервал, ожидаемый интервал), которая возвращает значение для распределения хи-квадрат (у2), т.е. - вероятность, с которой статистика не принадлежит критической области (нет оснований отвергать гипотезу). Аргумент фактический интервал есть массив эмпирических частот. Аргумент ожидаемый интервал есть массив теоретических частот.

 

При проверке гипотезы о нормальном распределении генеральной совокупности можно применить функцию НОРМАЛИЗАЦИЯ, которая выдает стандартизованную нормальную величину, функцию НОРМСТРАСП, которая выдает значение функции распределения стандартизованной величины. Можно сразу применить функцию НОРМРАСП, которая выдает функцию распределения случайной величины, если аргумент интегральный=1, и плотность распределения случайной величины, если аргумент интегральный=0.

 

При проверке гипотезы о биноминальном распределении может оказаться полезной функция БИНОМРАСП, которая выдает функцию распределения случайной величины, если аргумент интегральный=1, и , если аргумент интегральный=0.

 

При проверке гипотезы об однородности двух выборок (критерий Уилкоксона) упорядочить по возрастанию можно с помощью меню Данные/Сортировка или кнопки меню сортировка по возрастанию .

 

СОДЕРЖАНИЕ ОТЧЕТА

1. Краткое описание методов, применяемых при выполнении задания.

2. Описание порядка выполнения задания.

3. Анализ полученных результатов.

 

Литература

Основная литература

1. Бочаров П.П., Печинкин А.В. Теория вероятностей. Математическая статистика. – М.: Высшая школа, 1999.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1999.

3. Вентцель А.С. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1997.

4. Кремер Н.К. Теория вероятностей и математическая статистика. - М.: Юнити-ДАНА, 2000.

 

Дополнительная литература

 

1. Бугров Я.С., Никольский С.М. Краткий курс теории вероятностей и математической стати­стики. - М.: Наука, 1987.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 1999.

3. Кочетков В.Е. Краткий курс высшей математики. - М.: РИЦ МГИУ, 2000.

4. Мантуров О.В., Матвеев Н.М. Курс высшей математики. - М.: Высшая школа, 1986.

5. Солодовников А.С. Теория вероятностей. - М.: Просвещение, 1982.