24. ТИПИЧНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
1. Равномерное распределение.
Закон распределения непрерывной СВ, задаваемый формулой
 (
( ) (24.1)
) (24.1)
называется равномерным распределением с параметрами 
Графиком равномерного распределения является горизонтальный отрезок (рис. 24.1).
Пример: равномерному закону распределения (24.1) подчиняется СВ  ошибка, возникающая при округлении числа.
ошибка, возникающая при округлении числа.
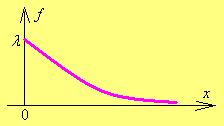

Рис. 24.1 Рис. 24.2
2. Показательное распределение.
Закон распределения непрерывной СВ, задаваемый формулой
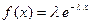 (
( ) (24.2)
) (24.2)
называется показательным (экспоненциальным) распределением с параметром 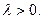
График показательного распределения – ниспадающая линия (рис. 24.2).
Пример: показательному закону распределения (24.2) подчиняется СВ  время работы прибора до его поломки.
время работы прибора до его поломки.
3. Нормальное распределение.
Закон распределения непрерывной СВ, задаваемый формулой

 (24.3)
(24.3)
называется нормальным распределением с параметрами 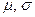

 Графиком нормального распределения является колоколообразная линия (рис. 24.3). Случайная величина
Графиком нормального распределения является колоколообразная линия (рис. 24.3). Случайная величина  подчиняющаяся нормальному закону распределения (24.3), называется нормальной.
подчиняющаяся нормальному закону распределения (24.3), называется нормальной.
Пример: нормальному закону распределения подчиняется СВ  отклонение пробоин от центра мишени.
отклонение пробоин от центра мишени.
Нормальное распределение встречается наиболее часто. Покажем, что функция распределения нормальной СВ есть функция Лапласа Рис. 24.3
 , (24.4)
, (24.4)
о которой говорилось в разделе 16.
¨ 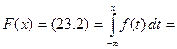
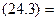

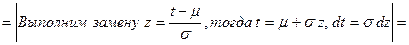
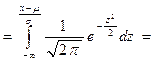

 ■
■
Оказывается, что
Если  нормальная СВ, нормальная СВ,
|
то 
|
где  функция Лапласа. функция Лапласа.
|
(24.5)
¨ 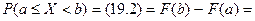

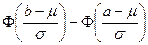 . ■
. ■
25. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Хотя закон распределения даёт полную информацию о СВ, но для практических нужд достаточно знать лишь некоторые числа, дающие общее представление о СВ. К таким числам, называемым числовыми характеристиками СВ  относятся в первую очередь математическое ожидание
относятся в первую очередь математическое ожидание  дисперсия
дисперсия  и среднеквадратичное отклонение
и среднеквадратичное отклонение 
1. Математическим ожиданием (средним значением) СВ  называется число
называется число  определяемое по формуле
определяемое по формуле
 (25.1)
(25.1)
З а д а ч а 1. СВ  имеет следующий закон распределения
имеет следующий закон распределения

| 5 6 7 8 |

| 0,2 0,25 0,35 0,2 |
Найти 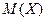 и
и 
□ Здесь СВ  дискретна, поэтому
дискретна, поэтому


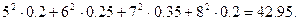 ■
■
З а д а ч а 2. СВ  имеет плотность вероятности
имеет плотность вероятности 
Найти 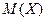 и
и 
□ Здесь СВ  непрерывна, поэтому
непрерывна, поэтому
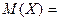

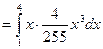

 ■
■
Укажем свойства математического ожидания:
♦ 1. 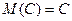

♦ 2. 
♦ 3.  (только для независимых
(только для независимых  и
и  ).
).
2. Дисперсией СВ  называется число
называется число  определяемое формулой
определяемое формулой

|
(25.2)
С помощью (27.1) это равенство можно записать так

Укажем свойства дисперсии:
♦ 1. 
♦ 2. 
♦ 3. 
♦ 4.  (только для независимых
(только для независимых  и
и  ),
),
♦ 5.  (25.3)
(25.3)
Формула (27.3) иногда бывает удобней формулы (27.2).
3. Среднеквадратичным отклонением СВ  называется число
называется число  определяемое по формуле
определяемое по формуле
 (25.4)
(25.4)
Числа 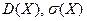 дают представление о том, как далеко разбросаны, рассеяны значения СВ вокруг своего среднего значения. Число
дают представление о том, как далеко разбросаны, рассеяны значения СВ вокруг своего среднего значения. Число 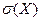 имеет ту же размерность, что и
имеет ту же размерность, что и 
З а д а ч а 3. Найти 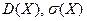 для СВ, заданной в задаче 1.
для СВ, заданной в задаче 1.
□ В задаче 1 было найдено, что  отсюда
отсюда 

 ■
■
26. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ТИПИЧНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
1. СВ  распределённая по биномиальному закону
распределённая по биномиальному закону
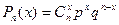 (
( )
)
имеет следующие числовые характеристики

 (26.1)
(26.1)
З а д а ч а 1. Автомобиль, подъехав к перекрёстку, может продолжить движение по любой из трёх дорог: А, В или С с одинаковой вероятностью. К перекрёстку подъехало 4 автомобиля. Найти среднее число автомобилей, которое поедет по дороге В и вероятность того, что по дороге А поедут 2 автомобиля.
□ Дано: 
 вероятность того, что автомобиль поедет по дороге В.
вероятность того, что автомобиль поедет по дороге В.
Пусть  количество автомобилей, которые поедут по дороге В.
количество автомобилей, которые поедут по дороге В.
Тогда среднее число будет равно 
Вероятность того, что по дороге А поедут 2 автомобиля, равна
 ■
■
2. СВ  распределённая по закону Пуассона
распределённая по закону Пуассона


имеет следующие числовые характеристики

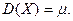 (26.2)
(26.2)
Здесь  есть среднее число событий, происходящих за определённое время
есть среднее число событий, происходящих за определённое время 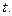
Если дана постоянная величина 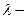 среднее число событий, происходящих в единицу времени, то
среднее число событий, происходящих в единицу времени, то 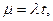 тогда
тогда
 (26.3)
(26.3)
вероятность того, что за время 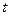 произойдёт
произойдёт  событий.
событий.
З а д а ч а 2. Пусть к концу рабочего дня среднее число телефонных звонков равно 2 в минуту. Какова вероятность того, что
а) за 2 минуты не поступит ни одного звонка?
б) за 3 минуты поступят 5 звонков?
□ Дано: 
а) 
 Тогда
Тогда 
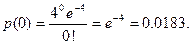
б) 
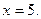 Тогда
Тогда 
 ■
■
3. СВ  имеющая равномерный закон распределения
имеющая равномерный закон распределения
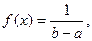

имеет следующие числовые характеристики

 (26.4)
(26.4)
4. СВ  распределённая по показательному закону
распределённая по показательному закону
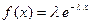 (
( )
)
имеет следующие числовые характеристики

 (26.5)
(26.5)
5. СВ  распределённая по нормальному закону
распределённая по нормальному закону
 (
( )
)
имеет следующие числовые характеристики

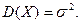 (26.6)
(26.6)
Отсюда 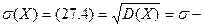 среднеквадратичное отклонение.
среднеквадратичное отклонение.
27. КОВАРИАЦИЯ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Величина
 (27.1)
(27.1)
называется ковариацией (или корреляционным моментом).
Если  независимые СВ, то
независимые СВ, то 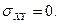
Безразмерная величина
 (27.2)
(27.2)
называется коэффициентом корреляции.
Основное свойство коэффициента корреляции:

Если  то СВ
то СВ  называются некоррелированными (взаимно несвязанными). Чем ближе
называются некоррелированными (взаимно несвязанными). Чем ближе  к
к 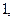 тем сильнее связь между
тем сильнее связь между  и
и 
28. ЛИНЕЙНАЯ РЕГРЕССИЯ
Даны зависимые СВ  и
и  но вид зависимости неизвестен. Попробуем выбрать такую функцию
но вид зависимости неизвестен. Попробуем выбрать такую функцию 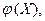 чтобы отклонение
чтобы отклонение  от
от  было минимальным.
было минимальным.
В качестве меры отклонения возьмём величину 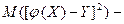 среднее значение квадрата отклонения.
среднее значение квадрата отклонения.
Функция  называется регрессией
называется регрессией  по
по 
Выберем линейную функцию

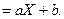 (28.1)
(28.1)
Искомые коэффициенты  должны быть такими, чтобы величина
должны быть такими, чтобы величина
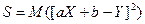 (28.2)
(28.2)
была минимальной. Минимум достигается тогда, когда


Сначала преобразуем (31.2).
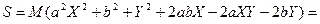

Отсюда
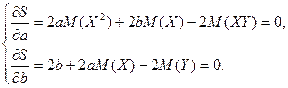
Сократим на 2 и перенесём свободные члены в правую часть.

Из второго уравнения системы имеем  (а)
(а)
Поставим (а) в (31.1 ):

 (28.3)
(28.3)
Это – уравнение линейной регрессии  по
по 
При  будет
будет 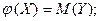 это значит, что график функции
это значит, что график функции  проходит через точку с координатами
проходит через точку с координатами 
Подстановка (а) в первое уравнение системы даёт
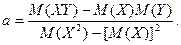 (28.3)
(28.3)
Число  называется коэффициентом регрессии.
называется коэффициентом регрессии.
Применив формулы (30.1) и (27.3), получим
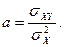
Но согласно (30.2)  поэтому
поэтому

Величины  и
и  имеют одинаковые знаки, поэтому при
имеют одинаковые знаки, поэтому при  величина
величина  растёт, при
растёт, при  величина
величина  убывает.
убывает.
Вопросы к экзамену.
1.Функция распределения вероятностей случайной величины, её свойства и график.
2.Плотность распределения вероятностей непрерывной случайной величины, её свойства и график. Равномерное распределение.
3.Числовые характеристики непрерывных случайных величин (математическое ожидание, дисперсия, среднее квадратическое отклонение).
4.Нормальное распределение.
5.Показательное распределение. Функция надёжности.






