Задание 1. Получить эмпирическую формулу линейной регрессии, решая систему уравнений с помощью встроенных функций. Сравнить результаты. Оценить тесноту связи. Построить графики. С помощью полученного уравнения найти значение y в точке x=n+0.55, где n – номер варианта.
Решение в программе Excel
По заданным парам значений
| x | 45,1 | 59,0 | 57,2 | 61,8 | 58,8 | 47,2 | 55,2 |
| y | 68,8 | 61,2 | 59,9 | 56,7 | 55,0 | 54,3 | 49,3 |
рассчитать параметры линейной функции y=a+bx. Оценить тесноту связи.
Р е ш е н и е
Для расчета параметров a, b линейной регрессии y=a+bx решаем систему линейных уравнений
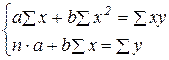
По исходным данным рассчитываем 
.
| x | y | xy | x2 | y2 | |
| 45,1 | 68,8 | 3102,88 | 2034,01 | 4733,44 | |
| 59,0 | 61,2 | 3610,80 | 3481,00 | 3745,44 | |
| 57,2 | 59,9 | 3426,28 | 3271,84 | 3588,01 | |
| 61,8 | 56,7 | 3504,06 | 3819,24 | 3214,89 | |
| 58,8 | 55,0 | 3234,00 | 3457,44 | 3025,00 | |
| 47,2 | 54,3 | 2562,96 | 2227,84 | 2948,49 | |
| 55,2 | 49,3 | 2721,36 | 3047,04 | 2430,49 | |
| сумма | 384,3 | 405,2 | 22162,34 | 21338,41 | 23685,76 |
,
откуда a=76,88, b=-0,35.
Уравнение регрессии: y=76.88-0.35x.
Чтобы оценить тесноту связи, рассчитаем коэффициент детерминации 
, где
- линейный коэффициент парной корреляции;
σх - среднее квадратическое отклонение x;
- среднее квадратов значений x;
- квадрат среднего значения x;
σу - среднее квадратическое отклонение y;
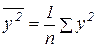- среднее квадратов значений y;
- квадрат среднего значения y.
В нашем случае получим
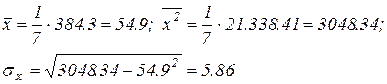
Аналогично получаем σу =5,74.
Тогда 
; 
.
Т.о. лишь 12,7% изменения результата y объясняется изменением фактора x. Коэффициент корреляции rxy между рядами данных x и y можно также вычислить с помощью статистической функции КОРЕЛЛ.
Для получения линий регрессии и их уравнений можно использовать так называемые линии тренда для диаграмм. По заданным значениям (x;y) построим диаграмму (на рис. 1 построена точечная диаграмма). С помощью щелчка правой клавиши мыши по элементам полученной диаграммы (точкам, столбцам и т.п.) активировать меню, в котором выбрать команду ДОБАВИТЬ ЛИНИЮ ТРЕНДА. Откроется диалог ЛИНИЯ ТРЕНДА. Выберем линейный тренд. Кроме того, открыв закладку ПАРАМЕТРЫ и установив флажки показывать уравнение на диаграмме и поместить на диаграмме величину достоверности аппроксимации, можно получить уравнение регрессии и коэффициент детерминации R2.
Уравнение линейной регрессии можно также получить с помощью встроенной функции, причем в этом случае будет выводиться дополнительная регрессионная статистика. Рассмотрим этот способ подробнее.
Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии y=a+bx. Порядок вычисления следующий:
1) введите исходные данные;
2) выделите область пустых ячеек 5 
2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1 2 – для получения только оценок коэффициентов регрессии;
3) активизируйте Мастер функций и в категории Статистические выберите функцию ЛИНЕЙН;
4) заполните аргументы функции:
5) известные значения у – диапазон, содержащий данные результативного признака;
известные значения х – диапазон, содержащий данные независимого признака;
константа – логическое значение, которое указывает на наличие или отсутствие свободного члена в уравнении; если константа=1, то свободный член рассчитывается обычным образом, если константа=0, то свободный член равен 0;
статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если статистика=1, то дополнительная информация выводится, если статистика=0, то выводятся только параметры уравнения;
6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Среднеквадратическое отклонение b | Среднеквадратическое отклонение a |
| Коэффициент детерминации R2 | Среднеквадратическое отклонение y |
| F -статистика | Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
