Парная регрессия – уравнение связи двух переменных y и x
y=f(x)
y – зависимая переменная; x – независимая, объясняющая переменная.
Различают линейные и нелинейные регрессии.
Линейная регрессия: y=a+bx+ε
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим параметрам:
² полиномы разных степеней y=a+b1x+b2x2+b3x3+ε
² равносторонняя гипербола 
Регрессии, нелинейные по оцениваемым параметрам:
² показательная 
² степенная 
² экспоненциальная 
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, применяют метод наименьших квадратов (МНК). В МНК подбирают параметры искомой формулы 
таким образом, чтобы сумма квадратов отклонений фактических значений зависимой переменной y от теоретических значений yf, вычисленных по формуле, минимальна, т.е.
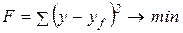
Если величину F рассматривать как функцию нескольких переменных
F(a, b,...) и воспользоваться теорией экстремумов, то при предположении о дифференцируемости f получаются необходимые условия для определения параметров a, b...:
Если, в частности, выбрать в качестве y=f(x) линейную зависимость y=a+bx, то задача сводится к нахождению точки минимума функции 
. Если точка минимума существует, то она является критической, т.е.
.
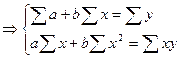Таким образом, для нахождения параметров линейной регрессии y=a+bx получена система уравнений (n – число заданных пар значений xi;yi)
.
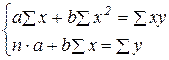Легко получить и другую форму записи решения. Очевидно, что совокупность равенств yi=a+bxi может быть записана в виде AZ=Y, где первый столбец матрицы А есть столбец исходных данных yi, Z – столбец искомых параметров регрессии a, b, столбец Y –столбец исходных данных xi:
Тогда легко показать, что Z=(ATA)-1ATY.
В некоторых случаях для оценки параметров уравнений нелинейной регрессии можно использовать систему уравнений для получения параметров линейной регрессии. Рассмотрим подробнее некоторые случаи:
² построению степенной модели 
предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
где 
² построению уравнения показательной кривой 
предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:
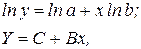
где 
² уравнение равносторонней гиперболы 
линеаризуется при замене 
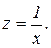Тогда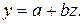 
² уравнение гиперболы 
линеаризуется при замене 
. Тогда 
.
² уравнение 
линеаризуется при замене 
. Тогда .
Множественная регрессия – уравнение связи с несколькими независимыми переменными
y=f(x1, x2,,..., xp),
y – зависимая переменная; xi – независимые, объясняющие переменные.
Для построения уравнения множественной регрессии чаще используются следующие функции:
² линейная y=a+b1x1+b2x2+...+bpxp
² степенная 
² экспонента 
² гипербола 
.
Можно использовать и другие функции, приводимые к линейному виду.
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов. Для линейных уравнений и нелинейных уравнений, приводимых к линейным, составляется система линейных уравнений, решение которой позволяет получить коэффициенты уравнения регрессии:
