Плоское движение твердых тел

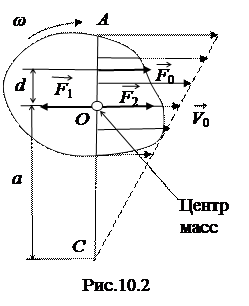
Пусть к телу, как будто плавающему на поверхности воды, в некоторой точке приложена сила F ₀ (рис. 10.2). Мысленно приложим к особой точке тела, называемой центром масс, две равные и противоположные силы F ₁ и F ₂, параллельные и равные силе F ₀. Под действием силы F ₂, тело совершает поступательное движение. А пара сил F ₀ и F ₁создает момент сил M ₀ =F ₀ d, под действием которого тело вращается.

Итак, плоское движение тела можно представить как сумму двух движений: поступательного со скоростью центра масс и вращения вокруг оси, проходящей через центр масс под действием результирующей пар сил.

Возможно другое представление плоского движения. Пусть скорость точки О – центра масс тела равна 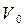(рис. 10.2). Проведём в плоскости движения перпендикуляр АОС к вектору скорости V ₀. Так как тело твёрдое, то огибающая линия концов векторов скоростей точек является прямой линией. Она и перпендикуляр пересекутся в некоторой точке С, скорость которой равна нулю. Через неё проходит так называемая мгновенная ось вращения, относительно которой тело совершает только вращательное движение с угловой скоростью 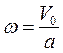. Положение мгновенной оси со временем меняется.

Примером плоского движения является качение колеса по рельсу. Если проскальзывания нет, то мгновенная ось вращения совпадает с линией касания колесной пары с рельсами, и перемещается со скоростью вагона.

Соответственно двум способам представления плоское движение может быть описано: либо уравнением основного закона динамики вращательного движения относительно мгновенной оси

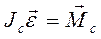, (10.3)

либо системой двух уравнений: второго закона Ньютона для поступательного движения тела как материальной точки, расположенной в центре масс, и основного закона динамики вращательного движения тела относительно оси, проходящей через центр масс

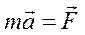и 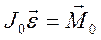(10.4)

В уравнениях J ₀ и J_с – моменты инерции тела относительно выбранных осей вращения О или С. Соотношение между моментами инерции тела относительно осей О или С определяют по теореме Штейнера.

Теорема Штейнера

Момент инерции является мерой инертности тела при вращательном движении и по определению равен сумме произведений масс частиц тела m_i на квадраты их расстояний r до оси вращения:

. (10.5)

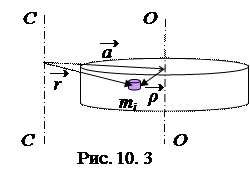Представим вектор от оси С– С до некоторой точки массы m_i как сумму векторов (рис. 10.3). Подставив в определяющую формулу момента инерции (10.5) радиус - вектор r и возведя сумму в квадрат, получим

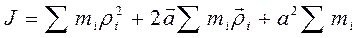. (10.6)

Первый член этого уравнения J ₀ – момент инерции тела относительно оси О – О, проходящей через центр масс. Во втором члене сумма определяет положение центра масс относительно оси О – О, и так как ось проходит через центр масс, то эта сумма равна нулю. Третий член – это произведение суммы масс частиц (то есть массы тела) на квадрат расстояния между осями. Итак, момент инерции равен

J_с = J ₀ + m а ². (10.7)

Это уравнение теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, и произведению массы тела на квадрат расстояния между осями.

В тех случаях, когда момент инерции относительно оси, проходящей через центр масс J ₀ , можно сравнительно легко рассчитать, теорема Штейнера позволяет определить момент инерции относительно произвольной оси J_с, избежав весьма трудоемких расчетов.