Силы давления – натяжения в автосцепках вагонов являются для поезда внутренними силами. Их можно определить, только расчленив поезд по автосцепке и рассматривая движение или хвостовой, или головной части поезда с учетом силы давления или натяжения в автосцепке между частями поезда.
Уравнение второго закона Ньютона для движения хвостовых вагонов: произведение массы вагонов на ускорение равно векторной сумме всех действующих сил:
. (5.7)
Спроецируем уравнение движения на оси координат
Ох: Δ Ma = Fнат –Fсопр – Δ Mg sin α, (5.8)
Oy: 0 = N – Δ Mg cosa. (5.9)
Обозначим уклон пути sin α = i. Учтем, что cos α ≥ 0,99995 = 1. Примем силу сопротивления качению колес по закону трения Fсопр=μсопрN = μсопр Δ Mg.
Рассмотрим сначала торможение поезда всеми колесами. В уравнение (5.7) второго закона Ньютона для хвостовой части поезда войдет сила давления на ее передний вагон и сила торможения. В проекции на ось Ох1 (пунктир на рис. 5.5) с учетом формулы предельной силы при экстренном торможении Fторм,пред = μсц Δ Mg, уравнениепримет вид
Δ М a = μсц Δ Mg + μсопр Δ Mg + Δ M g i+Fдавл.. (5.10)
Подставив формулу ускорения, полученную в главе 3 для экстренного торможении поезда, aмакс = g (mсц +mсопр +i), получим парадоксальный на первый взгляд результат: сила давления в автосцепках тормозящего поезда отсутствует, и равна нулю даже в условиях экстренного торможения. Правда, при идентичных условиях торможения всех колес.
Рассмотрим силы давления в автосцепках в условиях торможения поезда только локомотивом.В этих условиях отсутствует сила торможения самих вагонов, их тормозные колодки не прижаты к бандажам колес. Хвостовая часть напирает на головную часть поезда. Замедление хвостовой части состава происходит под действием силы давления передней части состава, силы сопротивления качению и скатывающей силы. Из уравнения движения хвостовой части в проекции на координатную ось Ох1, направленную по вектору ускорения, против хода поезда (рис. 5.4), получим
Fдавл = Δ Ma – (μсопр+i)Δ Mg. (5.11)
Силы давления возрастают с увеличением ускорения при торможении. К хвосту состава, с уменьшением массы рассматриваемой части состава, сила давления в автосцепках уменьшается почти по линейному закону. Наибольшая сила давления действует в автосцепке между первым вагоном и локомотивом. Поэтому впереди ставят наиболее нагруженные вагоны.
Задачи
1. Определить, при какой скорости опрокинется вагон на повороте радиусом 600 м, если наружный рельс выше внутреннего на 5 см. Центр тяжести вагона на высоте 1,7 м.Ширина колеи 1,520 м.
2. Определить, на сколько наружный рельс должен быть выше внутреннего на повороте дороги радиусом 600 м при скорости движения поезда 15 м/с. Ширина колеи 1,520 м.
3. Определить, с какой боковой силой действуют колеса вагона массой 60 т на рельсы на повороте дороги радиусом 600 м при скорости движения
20 м/с, если расчетная скорость движения 15 м/с. Определить величину непогашенного ускорения.
4.Определить силу натяжения в автосцепке локомотива и силу натяжения в автосцепке последнего вагона при движении поезда с ускорением 0,2 м/с2. Масса состава 2000 т, масса вагона 40 т, коэффициент сопротивления 0,003.
5. Вагон массой 60 т на стрелке изменил направление движения на
5 градусов за 5 секунд. Определить центробежную силу, действующую на вагон при скорости движения 10 м/с. Определить силу бокового давления на стрелку.
6. Платформа при скорости 10 м/с на стрелке изменила направление движения на 5 градусов за 5 секунд. Определить силу трения, действующую на контейнер массой 10 т. Будет ли скользить незакрепленный контейнер, если коэффициент трения 0,20.
7. Под каким углом к вертикали стоит пассажир в вагоне, движущимся на повороте радиусом 400 м с расчетной скоростью.
6. СТАТИКА
Статика – это раздел механики, изучающий условия равновесия материальных тел под воздействием сил, действующих на тела. В задачах статики предполагается, что тела являются абсолютно твердыми, для которых расстояние между любыми точками постоянно.
Условие равновесия тел
Равновесием называется такое состояние тела, при котором оно находится в состоянии покоя относительно системы отсчета.
Возможны состояния устойчивого, неустойчивого и безразличного равновесия. При устойчивом равновесии тело, выведенное из положения равновесия внешним воздействием, возвращается обратно к положению равновесия после снятия воздействия. Например, шарик в сферическом углублении после толчка возвращается на дно. Шарик на вершине сферического купола находится в состоянии неустойчивого равновесия, так как достаточно незначительного смещения, чтобы шарик скатился. Примером безразличного равновесия может быть положение шарика на горизонтальной поверхности.
Рассмотрим три примера равновесия тел.
1. Пусть на тело действует несколько сил, линии действия которых пересекаются в одной точке. Это условие выполняется всегда, если тело можно считать материальной точкой. Пусть равнодействующая сила, равная векторной сумме всех сил, равна нулю. Тогда, согласно первому закону Ньютона, тело будет находиться в покое (если перед этим оно не двигалось равномерно и прямолинейно). Это условие отсутствия поступательного движения тела, является уравнением равновесия
. (6.1)
Спроецируем уравнение равновесия на оси координат 
. Для равновесия тела под действием системы сходящихся сил достаточно, чтобы суммы проекций этих сил на каждую из трёх осей координат были бы равны нулю.
2. Пусть тело имеет ось вращения, которая установлена в неподвижных подшипниках. Пусть на тело действует некоторая сила F. Поступательного перемещения тела не будет, так как этому препятствуют подшипники, которые действуют на ось с силами реакции. Возникающие силы реакции компенсируют силу F так, чтобы сумма сил была бы равна нулю. Если линия действия силы проходит через ось вращения, то тело будет находиться в состоянии равновесия. Однако, как известно из опыта, если внешняя сила не проходит через ось вращения, то её действие приведет к вращению тела относительно оси. Вращающее воздействие силы характеризуется моментом силы. Момент силы будет тем больше, чем больше величина силы и чем больше плечо силы: 
. Плечом силы называется длина перпендикуляра, опущенного из оси вращения на линию действия силы. Условно принимают: если сила вращает тело по часовой стрелке, то момент силы положительный, а если против часовой стрелки, то отрицательный.
Пусть точка приложения силы определяется радиус-вектором r, проведенным из оси,тогда плечо силы равно 
, а момент силы равен 
(рис. 6.1). Очевидно, здесь записано векторное произведение 
. Вектор момента силы относительно оси принимают за аксиальный вектор, то есть вектор, направленный по оси вращения согласно правилу векторного произведения. Направление вектора момента силы можно также определить правилом буравчика: если вращать ручки буравчика под воздействием силы, то направление вектора момента силы совпадает с поступательным движением буравчика по оси.
Если на тело действует несколько сил, то вращения не будет, если сумма моментов сил относительно оси будет равна нулю:
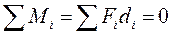(6.2)
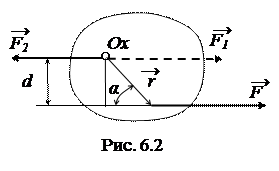
3. Рассмотрим свободное тело, которое не ограничено в своем движении другими твердыми телами. Выберем некоторый центр, в котором расположим начало координатных осей. Пусть на тело действует несколько сил, точки приложения которых относительно, например, оси Ох, определяются их радиус-векторами (ось на рис.6.2 направлена за чертеж). Вектора сил можно перемещать по их линии действия. Но чтобы переместить вектор силы перпендикулярно линии действия к оси, надо для компенсации к этой оси приложить равную, противоположно направленную силу F 2. Таким образом, действие произвольной силы на тело можно представить равной ей силой F 1, приложенной к произвольно выбранной оси и вращающему моменту пары сил F–F 2. Вращающий момент пары равных, противоположно направленных сил не зависит от выбора оси вращения и равен произведению одной из сил на плечо пары 
. Плечо пары сил равно расстоянию между линиями действия сил 
. Момент пары сил можно представить аксиальным вектором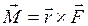 
, перпендикулярным плоскости пары сил.
Итак, тело не будет перемещаться поступательно, если векторная сумма сил, приложенных к произвольному центру, будет равна нулю. Тело не будет вращаться относительно выбранных осей, если сумма моментов пар сил будет равна нулю:
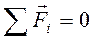и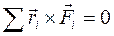 
. (6.3)
При решении задач статики выбирают положение центра и декартовых осей координат так, чтобы решение задачи было наиболее простым. Записывают уравнения (6.3) в проекции на эти оси. Получают шесть алгебраических уравнений для твердого тела, имеющего шесть степеней свободы (трёх координат центра и трёх углов поворота).
