Любая точка твердого тела при вращении движется поступательно по круговой траектории. Однако параметры поступательного движения (путь, скорость, ускорение) для разных точек тела являются различными. Общим параметром движения будет угол поворота тела вокруг оси. Для любой точки тела это угловой путь φ. Радиус-вектор проводится из центра окружности в точку. В системе СИ угловой путь измеряется в радианах.
Быстроту изменения углового пути характеризуют угловой скоростью. Мгновенное значение угловой скорости равно отношению изменения угла поворота за бесконечно малое время ко времени поворота:
. (9.1)
То есть угловая скорость равна первой производной от угла поворота по времени.
Для указания направления вращения угловую скорость считают аксиальным вектором, то есть вектором, направленным по оси вращения. Направление вектора угловой скорости можно определить правилом буравчика: если буравчик вращать вместе с телом, то направление поступательного движения буравчика совпадает с вектором угловой скорости. Единица измерения угловой скорости в СИ радиан в секунду (рад/с).
Быстроту изменения угловой скорости характеризуют угловым ускорением. Угловое ускорение равно отношению изменения угловой скорости за бесконечно малое время ко времени этого изменения:
. (9.2)
То есть угловое ускорение равно первой производной от угловой скорости по времени. Угловое ускорение, как и угловая скорость, является аксиальным вектором. Если скорость вращения увеличивается, то вектор углового ускорения направлен по вектору угловой скорости, при торможении – наоборот. Единица измерения в СИ (рад/с2).
Применяются внесистемные единицы измерения. Угловой путь измеряют как число оборотов тела вокруг оси N. Так как в одном обороте 2 π радиан, то 
. Скорость вращения характеризуют частотой, то есть числом оборотов за единицу времени (за одну секунду или за одну минуту). Соотношение с угловой скоростью будет 
или 
.
Между параметрами поступательного и вращательного движения точки тела существует связь. Путь точки – это длина дуги окружности, равная произведению угла поворота на радиус окружности 
. Определив первую производную по времени, получим формулу для скорости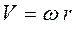 
. Чтобы соблюдалось соотношение между векторами линейной и угловой скорости, его записывают в виде векторного произведения
. (9.3)
Тангенциальное ускорение точки определим как первую производную от скорости: 
. Нормальное ускорение 
.
При равнопеременном вращательном движении, то есть с постоянным угловым ускорением, формулы углового пути и скорости аналогичны формулам при поступательном равнопеременном движении
. (9.4)
Момент силы
Сила, приложенная в некоторой точке твердого тела, закрепленного на неподвижной оси, приводит к вращению тела вокруг оси, если она создает вращающий момент сил. Как видно (рис. 9.2), вращает только та составляющая силы, которая перпендикулярна радиус-вектору точки приложения силы 
. Другие составляющие силы компенсируются силами в подшипниках оси.
Вращающее воздействие силы будет тем больше, чем дальше от оси приложена сила. Таким образом, определим момент силы как произведение радиус-вектора на вращающую часть силы: 
. Произведение 
равно длине перпендикуляра, опущенного из оси вращения на линию действия силы. Его называют плечом силы. Тогда момент силы можно определить как произведение силы на плечо силы 
. Момент силы относительно оси это аксиальный вектор, то есть вектор, направленный по оси вращения тела.
Вектор момент силы равен векторному произведению радиус-вектора точки приложения силы на вектор силы:
. (9.5)
Направление вектора момента силы определяется правилами векторного произведения: если смотреть с конца вектора момента силы, то направление поворота радиус-вектора по кратчайшему направлению к вектору силы должно происходить против часовой стрелки. Для определения направления вектора момента силы можно воспользоваться правилом буравчика: если вращать буравчик под воздействием силы, то направление вектора момента силы совпадает с поступательным движением буравчика. Итак, вращательное воздействие силы определяется не самой силой, а её моментом силы
