Определим силы давления на рельсы передних и задних колес (передней и задней вагонных тележек) вагона, стоящего на горизонтальном участке пути. Масса вагона m. Пусть центр тяжести вагона из-за неравномерной загрузки расположен на некотором расстоянии l от передней оси. Расстояние между осями вагона L (рис. 6.3). На вагон с грузом действуют со стороны Земли силы тяжести вагона m g и рельсы. Рельсы действуют в точках контакта с передними и задними колесами с силами нормального давления Nп и Nз.
Мысленно уберем рельсы. Вагон, висящий в пространстве под действием всех указанных сил, должен оставаться в равновесии. Он не должен ни перемещаться поступательно, ни вращаться. Запишем для вагона условие отсутствия поступательного движения: сумма проекций сил на вертикальную ось координат OY равна нулю:
Nп +Nз – m g = 0. (6.4)
В этом уравнении две неизвестные силы Nп и N3 – силы нормального давления рельсов на передние и задние колеса. Поэтому необходимо еще одно уравнение равновесия – условие отсутствия вращения. Как видно на рис. 6.4 силы, действующие на вагон, не сходятся в одной точке и, следовательно, создают вращающий момент сил. Видимой оси вращения нет на рисунке. Но это не важно. Где бы ни расположить возможную ось вращения, перпендикулярную плоскости рисунка, все равно сумма моментов сил для неподвижного вагона должна быть равна нулю. Выгодно ось вращения выбрать проходящей через точки опоры либо передних, либо задних колес. В этом случае плечи сил давления Nп или Nз будут равны нулю. Пусть ось проходит через точки опоры передних колес П. Моменты силы тяжести mg l действует относительно оси П против часовой стрелки. Будем считать его отрицательным. А момент силы давления рельсов на задние колеса NзL – по движению часовой стрелки – положительным. В итоге уравнение равновесия, то есть равенство нулю суммы моментов сил относительно оси П, будет
− m g l + N3 L = 0. (6.5)
Отсюда сила давления на задние колеса равна 
.
Подставив N3 в уравнение (6.5) или записав уравнение моментов сил относительно оси задней оси, получим 
.
Чем ближе к оси расположен центр тяжести, тем больше сила давления рельсов на эту колесную пару. Сила давления на передние и задние колеса будет одинакова и равна половине силы тяжести вагона, если центр масс находится посередине.
Рассмотрим режим ускоренного движения вагона. Очевидно, силы давления на колеса вагона со стороны рельсов Nп и Nз отличаются от полученных для неподвижного вагона. Выделим мысленно вагон из состава (рис. 6.4). Вагон покоится относительно поезда, но поезд является неинерциальной системой отсчета. Поэтому для соблюдения равновесия следует ввести силу инерции: 
. Сила инерции приложена к центру масс вагона и направлена против вектора ускорения.
Пусть центр масс вагона находится на расстоянии l от передней оси. Со стороны передней и задней частей состава на автосцепки вагона действуют силы натяжения Fп и Fз. При движении со стороны рельсов действует сила сопротивления качению колес: Fсопр=μсопрmg. Под действием указанных сил вагон должен оставаться в равновесии относительно поезда. Запишем уравнение равновесия вагона в проекции на ось Ох
Ох: –Fин+ (Fп– Fз) – Fсопр = 0.(6.6)
Запишем уравнения равновесия вагона под действием моментов сил относительно осей, проходящих через точки контакта передних и задних колес
–mgl+ Nз L+ (Fп –Fз) h – FинH = 0, (6.7)
mg (L–l)– Nп L+ (Fп – Fз) h – FинH = 0. (6.8)
Подставим из уравнения (6.6) разность сил натяжения. Тогда силы давления рельсов на передние и задние колеса вагона будут равны
, 
. (6.9)
Если сопоставить с результатами расчета для неподвижного вагона, то при движении с ускорением сила инерции разгружает передние колеса и нагружает задние колеса. А сила сопротивления – наоборот. Как и должно быть, сумма сил давления, несмотря на перераспределение их величин, равна силе тяжести вагона.
Стоянка поезда на спуске
Чтобы поезд не скатывался на спуске, необходимо создать силу торможения. Затормозить можно силами торможения колёс всего поезда, или только локомотива, или с помощью тормозного башмака. Тормозной башмак – это приспособление для торможения вагона, поезда, удержания их на спуске. Когда колесо накатывается на башмак, оно прижимает его к рельсу и сила сопротивления при качении колес заменяется силой трения покоя или силой трения скольжения башмака по рельсу. Эти силы значительно больше силы сопротивления качению и тормозят поезд более эффективно.
|
Определим силу торможения состава с башмаком (рис. 6.5). К оси колесной пары, под которой башмак, приложена скатывающая сила всего поезда Mgi, и сила тяжести части вагона Δ Mg cos α ≈ Δ Mg. Эти силы колесом передаются на упор башмака. Если равнодействующая этих сил Q проходит через упор башмака или ближе к нижней точке, то торможение поезда возможно.
Если линия равнодействующей силы проходит с наружной стороны упора, то момент скатывающей силы перевернет колесо через упор. Таким образом, условием предотвращения перескока через упор, является 
.
Рассмотрим равновесие башмака. На него действует со стороны колеса сила тяжести части вагона Δ Mg. Ее компенсирует сила нормального давления рельса на башмак. Предельное значение силы трения между башмаком и рельсом равно Fторм,пред= μсцN= μсц Δ Mg. Если скатывающая сила поезда будет больше предельной силы торможения, то поезд будет скользить на башмаке.
Наоборот, если скатывающая сила станет меньше предельной силы торможения, скольжение прекратится и башмак заклинит. При этом сила трения скольжения башмака по рельсу превратится в силу трения покоя, величина которой станет равна скатывающей силе: Fторм= Mgi. Итак, условие стоянки поезда на башмаке
μсц Δ Mg ≥ Mg. (6.10)
Например, если сила тяжести вагона, приходящаяся на одно колесо составляет четвертую часть силы тяжести вагона, то число вагонов состава, которую может еще удержать один башмак будет не более 
. При уклоне 0,005 при коэффициенте сцепления 0,24 число одинаковых вагонов в составе должно быть не более 12. Значит, для большого состава следует ставить несколько башмаков.
Балластировка локомотива
Сила давления или сила натяжения в автосцепке локомотива со стороны состава создает дополнительный момент сил, действующий на локомотив. При разгоне момент силы натяжения разгружает передние колеса. Недогруженные ведущие колеса локомотива с меньшей силой давят на рельсы и раньше других срываются на буксование. Задние колеса, наоборот, сильнее давят на рельсы, приводя к опасным напряжениям в зоне контакта. В итоге приходится ограничивать мощность тяговых двигателей. А в режиме торможения поезда одним локомотивом состав напирает на автосцепку локомотива.
Рассмотрим режим разгона. Для выравнивания сил давления колесных пар на рельсы применяется балластировка локомотива. Она заключается в погрузке балласта в кузов локомотива так, чтобы выровнять силы давления на все колеса. Поэтому балласт или агрегаты располагаются преимущественно в переднюю часть.
Определим, где должен быть расположен центр масс локомотива после балластировки. На локомотив в процессе движения действуют следующие силы: сила тяги, общая сила тяжести локомотива и балласта mg, силы нормального давления рельсов на все колесные пары Ni, которые по условию балластировки принимаем одинаковыми, и сила натяжения в автосцепке со стороны состава Т (рис. 6.7). Пусть к – число колесных пар. Пренебрежем силой инерции.
Согласно уравнениям статики локомотив в системе отсчета "поезд" будет находиться в равновесии, если сумма векторов всех сил будет равна нулю и сумма моментов сил относительно любой выбранной оси вращения будет равна нулю. Спроецируем уравнение равновесия локомотива на оси координат
О х: Fтяги – T = 0,(6.11)
O y: N 1 + N 2 + N 3 …+ Nк – mg = 0.(6.12)
Сумма моментов сил относительно любой оси должна быть равна нулю. Выберем, например, ось, проходящую через точки опоры задних колес.
–T h – N 2 l – N 32 l… – Nк (к –1) l + mg x = 0. (6.13)
Силы давления рельсов на колесные пары примем одинаковыми Ni = mg/k. Подставляя силу давления Ni и силу натяжения T = Fтяги = μсцmg, получим 
. Учтем, что сумма коэффициентов – членов арифметической прогрессии равна произведению половины суммы первого и последнего членов на число членов: k (k –1) / 2. В итоге получим 
Как видно, центр масс должен быть расположен ближе к носу локомотива на расстояние 
.
Задачи
1. Определить силу сжатия автосцепок первого и последнего вагонов состава, стоящего на спуске дороги с уклоном 0,005. Масса состава 2000 т, масса вагона 40 т. Тормозные башмаки под последним снизу вагоном.
2. Определить горизонтальную силу, достаточную, чтобы стронуть четырехосный вагон с места, если перед колесом ступенька высотой 3 1мм. Радиус колеса 0,51м. Масса вагона 20 т.
3. При наезде на препятствие последний вагон массой 60 т опрокинулся относительно передней тележки. Определить ускорение при торможении состава, если центр тяжести вагона на высоте 2 м посередине вагона, расстояние между осями крайних колес 15 м.
4. Опрокинется ли на повороте радиусом 600 м вагон массой 20 т силами давления 550 кН и 600 кН соседних вагонов. Расстояние между автосцепками 18 м. Центр масс вагона на высоте 1,8 м посередине, высота автосцепок 1,3 м.
5. Определить координаты центра масс вагона, нагруженного двумя контейнерами массой по 10 т и 18 т. Масса порожнего вагона 30 т, длина 18 м. Числа на рис.6.7 – расстояния в метрах до центров масс контейнеров и вагона.
6. Определить силы давления трех труб массой по 3 т на стенки и пол вагона, если ширина вагона 3,0 м, диаметр труб 1,26 м.
7. Какой вращающий момент сил должен создать тяговый двигатель, чтобы стронуть с места моторный вагон массой 20 т. Передаточное отношение равно 3,5. Радиус колеса 0,51 м, коэффициент сопротивления 0,005.
7. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
Три закона Ньютона являются важнейшими законами природы и позволяют решать любые задачи механики, достаточно только знать закономерности сил. Однако, если проинтегрировать уравнение второго закона Ньютона по времени взаимодействия тел, то можно прийти к понятию импульса, и если проинтегрировать по перемещению, то прийти к понятию энергии. Оказывается, что для замкнутых систем тел интегралы движения (импульс и энергия) обладают способностью сохраняться. Теперь даже не зная закономерностей для сил взаимодействия, используя законы сохранения, можно рассчитать параметры движения в процессе взаимодействия тел. Законы сохранения являются фундаментальными законами природы.
Закон сохранения импульса
Рассмотрим систему, состоящую из нескольких тел N. Запишем для некоторого тела уравнение второго закона Ньютона: изменение импульса тела равно импульсу силы, действующей на тело
. (7.1)
……………………………………………….
…………………………………………….
Здесь fi – равнодействующая всех внутренних сил. действующих на это тело со стороны других тел системы и Fi – равнодействующая сил со стороны внешних тел, не входящих в рассматриваемую систему. Индекс i – номер тела системы. Сложим все уравнения:
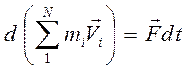. (7.2)
Здесь 
– сумма внешних сил. Внутренние силы, действующие попарно, сократились.
Рассмотрим замкнутую систему тел. Система тел называется замкнутой, если внешние силы или отсутствуют или взаимно компенсируют друг друга. Для замкнутой системы тел правая часть уравнения второго закона Ньютона для системы тел (7.2) равна нулю. То есть изменение суммы импульсов тел системы равно нулю, но это значит, что сама сумма импульсов тел постоянна. Отсюда следует один из важнейших законов природы – закон сохранения импульса: в замкнутой системе тел векторная сумма импульсов тел постоянна. Или иначе: в замкнутой системе тел сумма импульсов тел в начале процесса взаимодействия равна сумме импульсов тел после окончания процесса
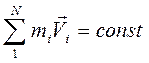или 
. (7.3)
Возможна ситуация, когда на какую либо координатную ось проекция векторной суммы внешних сил, действующая на систему тел, равна нулю. В этом случае, хотя импульс системы в целом не сохраняется, но сохраняется проекция импульса системы тел на эту ось.
Получим важное следствие закона сохранения импульса. Известно, что радиус-вектор центра масс системы из N тел определяется выражением 
. Здесь mi и ri – масса и радиус-вектор тела с номером i, m – масса системы тел. Продифференцируем по времени это выражение с учетом, что производная от радиус-вектора некоторого тела по времени это скорость тела. В результате получим 
. Отсюда следует: сумма импульсов тел равна произведению массы системы на скорость центра масс. Произведя замену в уравнении (7.2), получим уравнение второго закона Ньютона для движения центра масс
. (7.4)
Центр масс системы тел движется как материальная точка, в которой сосредоточена вся масса системы тел, под действием результирующей внешней силы.
Для замкнутой системы тел внешние силы или отсутствует, или скомпенсированы. Тогда центр масс движется в пространстве прямолинейно и равномерно. А если в начальный момент времени центр масс покоился, то его координаты будут постоянны, какие бы сложные движения не совершали отдельные тела системы.
Работа
Как экспериментально установлено, механическая работа, например, подъём воды из шахты воротом, зависит от силы тяжести и высоты подъема. Если ворот заторможен, то работа не совершается.
Пусть тело под действием постоянной силы 
совершает элементарное перемещение 
. Перемножим эти вектора скалярно и назовем их произведение элементарной работой
. (7.5)
Здесь угол α – угол между векторами силы и перемещения. Полная работа на конечном участке траектории равна сумме элементарных работ, то есть интегралу от силы по перемещению:
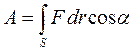. (7.6)
На графике зависимости проекции силы F cos α на направление перемещения элементарная работа равна площади узенькой заштрихованной полоски (рис. 7.1). Тогда полная работа, согласно графическому смыслу интеграла, будет равна площади графика. Единицей работы является джоуль (Дж = Н∙м).
Необходимость формального введения новой физической величины не самоочевидна, мало ли можно придумать комбинаций силы и перемещения. Только после введения через работу понятия энергии и, самое главное, доказательства способности энергии сохраняться, будет очевидно значение понятия работы.
Работа, обладая свойствами скалярного произведения, будет положительна, если угол между силой и перемещением острый, и отрицательна – если угол тупой. А если сила перпендикулярна перемещению, то работа не совершается. Например, при горизонтальном перемещении вагона сила тяжести работы не совершает.
Работу можно совершить быстро, а можно и медленно. Быстроту совершения работы характеризуют мощностью. Мощность равна отношению элементарной работы ко времени совершения работы:
. (7.7)
Мощность равна скалярному произведению силы на скорость точки приложения силы. Единицей мощности является ватт (Вт =Дж/с).
Например, паровая машина при одинаковой мощности с двигателем Дизеля имеет большую массу. Это обусловлено тем, что паровая машина является тихоходной и усилие на поршень должно быть большим для достижения необходимой мощности. Для повышения прочности приходится увеличивать размеры, массу.
Кинетическая энергия
Пусть тело перемещается под действием силы по горизонтальной плоскости, изменяя скорость от начальной V 1 до конечной V 2. Запишем, согласно определению, формулу работы силы при перемещении тела 
. Произведем преобразования: силу заменим произведением массы тела на ускорение (по второму закону Ньютона) 
, элементарное перемещение запишем 
. Подставим их под знак интеграла и после сокращения на dt получим уравнение
. (7.8)
Работа, оказывается, равна изменению некоторого параметра тела, который не зависит ни от формы траектории, ни от закона изменения силы вдоль траектории. Это важный для описания движения тела интеграл движения называют кинетической энергией поступательного движения
. (7.9)
Кинетическая энергия – это энергия движения. Кинетическая энергия всегда положительна. В разных системах отсчета скорость тела может принимать различные значения, поэтому кинетическая энергия тела зависит от выбора системы отсчета. Положительная работа силы приводит к повышению кинетической энергии тела. Уравнение (7.8) является теоремой о кинетической энергии: изменение кинетической энергии тела равно работе силы, действующей на тело.
Единицей энергии, как и работы, является джоуль (Дж).
Потенциальная энергия
Рассмотрим перемещение тела в поле силы тяжести по произвольной траектории (рис. 7.2). Определим работу силы тяжести как интеграл от скалярного произведения вектора силы тяжести на перемещение 
.
Как видно из рисунка, проекция элементарного вектора перемещения на направление силы тяжести равна уменьшению высоты тела над Землей 
. Тогда работа силы тяжести после взятия интеграла будет равна
. (7.10)
Работа в поле тяжести, оказывается, равна разности значений некоторого параметра, который не зависит от формы траектории. Этот интеграл движения называют потенциальной энергией
. (7.11)
Высота тела отсчитывается от некоторого, взятого произвольно, горизонтального уровня отсчета, так как при решении задач механики важно знать не абсолютное значение потенциальной энергии, а её изменение. Формула справедлива в области небольших, по сравнению с радиусом Земли, высот, пока ускорение свободного падения можно считать постоянным. Знак минус означает, что положительная работа совершается за счет уменьшения потенциальной энергии.
Получим формулу потенциальной энергии упругой деформации. В случае, когда тело деформируется под воздействием внешней силы, точка приложения силы перемещается и, значит, совершается работа. Если тело упругое и форма тела после выключения внешней силы восстанавливается, то работа упругих сил обращается в нуль. Значит, упруго деформированное тело обладает потенциальной энергией. Формулу для потенциальной энергии получим, определив работу сил упругости. Пусть выполняется закон Гука 
, где k– коэффициент упругости, х – деформация тела. Работа равна интегралу 
. Отсюда получим формулу потенциальной энергии упругой деформации
. (7.12)
Кроме поля тяжести работа сил поля не зависит от формы траектории и в других силовых полях. Например, в электростатическом поле, гравитационном поле. Такие поля называют потенциальными. При перемещении тела по замкнутой траектории, когда тело возвращается в исходную точку, работа в потенциальном поле равна нулю: 
. (Интеграл от силы по замкнутой траектории называется циркуляцией вектора силы).
Силы, работа которых не зависит от формы траектории, называют консервативными. В механике это силы тяжести, гравитационные силы, силы упругости.
Между силой и потенциальной энергией существует связь. Пусть тело перемещается вдоль линии действия силы на элементарное расстояние. Работа силы совершается за счет убыли потенциальной энергии: 
. Отсюда следует, что сила равна производной от потенциальной энергии по координате, направленной по линии действия силы, и взятой с обратным знаком
. (7.13)
Эта производная называется градиентом потенциальной энергии. То есть консервативная сила равна градиенту потенциальной энергии, взятому с обратным знаком 
.
Закон сохранения энергии
Рассмотрим замкнутую систему тел, в которой действуют консервативные силы. Под действием сил тела внутри системы перемещаются, совершается работа. Одна и та же положительная работа некоторой силы приводит к повышению кинетической энергии тела, но совершается за счет уменьшения потенциальной энергии этого тела в силовом поле других тел
и 
. (7.14)
Отсюда следует, что работа есть мера превращения энергии одного вида в другой вид. Приравняем правые части уравнений (7.14) и получим, что сумма кинетической и потенциальной энергии тела в состоянии «1» такая же, как в состоянии «2»: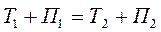 
, и вообще, в любом другом состоянии постоянна
(7.15)
Сумму кинетической и потенциальной энергий называют механической энергией. Если механическая энергия сохраняется для любого тела, то она сохраняется для всех тел замкнутой системы. Отсюда следует закон сохранения и превращения механической энергии: в замкнутой системе тел, между которыми действуют консервативные силы, механическая энергия постоянна.
В отличие от консервативных сил существуют так называемые диссипативные силы, работа которых приводит к диссипации (рассеянию) механической энергии. Диссипативными силами являются сила трения скольжения, силы вязкого трения между слоями при пластической деформации тел. Если в системе тел существуют диссипативные силы, то работа этих сил отрицательна на любом участке траектории, так как перемещение и сила всегда направлены противоположно. По теореме о кинетической энергии работа диссипативных сил равна уменьшению кинетической энергии. Но работа диссипативных сил не может изменить потенциальную энергию. Значит частично или полностью кинетическая энергия должна превратиться в эквивалентное количество другого вида энергии. Это внутренняя энергия. Например, при движении под действием силы трения скольжения кинетическая энергия тела как целого превращается в кинетическую энергию хаотического движения молекул тела, то есть во внутреннюю энергию.
Экспериментально в многочисленных опытах установлено, что в замкнутой системе тел полная энергия, равная сумме механической и внутренней энергий постоянна
. (7.16)
Это выражение закона сохранения и превращения полной энергии. Из закона следует, что при любых процессах внутри замкнутой системы тел различные виды энергии могут в эквивалентных количествах превращаться друг в друга, но их сумма постоянна. Энергия не создается и не уничтожается.
Из закона следует, что увеличение внутренней энергии равно уменьшению механической энергии системы тел, которое, в свою очередь, равно работе диссипативных сил:
. (7.17)
Закон сохранения полной энергии является фундаментальным законом природы, может самым важным. Он применим не только в механике, но и в любых процессах, протекающих в природе. Сомнения в выполнении закона сохранения энергии в истории науки были, (явление радиоактивности, открытие нейтрино) но в итоге явлений, в которых бы не сохранялась полная энергии, не обнаружено. В истории техники известно немало проектов создания вечного двигателя. Это машины, которые без поступления энергии извне могли бы сколь угодно долго совершать механическую работу. Закон сохранения энергии не позволил осуществиться этим проектам, сколь бы хитроумными они не были.
Задачи
1. Определить мощность, которую отдает электровоз в контактную сеть при рекуперативном движении с постоянной скоростью на спуске с уклоном 0,005. Масса поезда 2000 т, коэффициент сопротивления 0,002.
2. Определить расстояние, которое пройдет поезд массой 2500 т при коэффициенте сопротивления 0,004, если использовано 100 кг дизельного топлива с теплотворной способностью 46,1 МДж/кг. КПД двигателя 28 %.
 |
3. Определить теплоту, выделенную поездом массой 2000 т в режиме торможения (рис.7.3) на подъеме пути с уклоном 0,002. Определить коэффициент сцепления колес с рельсами.
4. Локомотив при мощности тяговых двигателей 6 МВт может везти поезд массой 2000 т по подъему со скоростью 36 км/час, а вниз со скоростью 54 км/час. Определить уклон пути и коэффициент сопротивления при качении колес.
5. Локомотив поочередно приводит в движение вагоны, растягивая их автосцепки. Пусть зависимость результирующей силы тяги и сопротивления от числа начавших движение вагонов имеет вид (рис.7.4). Определить максимальную массу состава, которую может везти локомотив, определить величину ускорения. Деформация автосцепки не превышает 5 см, масса вагона 50 т.
6. Определить, преодолеет ли подъем с уклоном 0,005 и длиной 5 км вагон массой 20 т. Начальная скорость 25 м/с. Определить величину и направление силы сцепления колес с рельсами. Коэффициент сопротивления качению 0,002.
7. Локомотив в режиме равномерного движения с постоянной мощностью везет состав из 20 вагонов со скоростью 20 м/с. Определить наибольшую скорость поезда, если два последних вагона отцепятся.
8. СОУДАРЕНИЕ ТЕЛ
Явление удара
Удар – это процесс кратковременного взаимодействия тел, при котором происходит значительное изменение скоростей тел, их импульсов. Силы удара могут быть сравнительно большими, так как, согласно второму закону Ньютона, изменение импульса тела равно импульсу силы: 
, и при малом времени удара D t сила удара F может быть большой. В этом случае действием внешних сил на время удара можно пренебречь и считать систему тел замкнутой. Поэтому для удара выполняется закон сохранения импульса: в замкнутой системе тел сумма импульсов постоянна, или сумма импульсов тел до взаимодействия равна сумме импульсов после взаимодействия
или 
. (8.1)
Явление удара осложнено такими процессами как излучение звуковых волн, распространение волн деформации в телах. Длительность удара можно оценить по времени отражения волн деформации. Например, молоток железнодорожный, в отличие от кувалды той же массы, имеет удлиненную форму. Поэтому время удара о забиваемый в шпалу костыль сравнительно больше, сила удара поменьше, а передаваемый костылю импульс тот же самый.
Существует две предельных идеализации реального удара: идеально упругий удар и абсолютно неупругий удар. При идеально упругом ударе тела в фазе сближения деформируются упруго, и часть кинетической энергии превращается в потенциальную энергию упругой деформации. Затем во второй фазе под действием упругих сил тела отталкиваются, форма тел восстанавливается, и потенциальная энергия деформации вновь превращается в кинетическую энергию. В результате при упругом ударе выполняется закон сохранения механической энергии.
При абсолютно неупругом ударе тела деформируются пластически. Удар заканчивается на фазе сближения, и затем тела движутся совместно, как одно целое. Это является признаком неупругого удара. Так как часть кинетической энергии превращается в работу пластической деформации, во внутреннюю энергию, то механическая энергия не сохраняется.
Соударение тел
Неупругий удар
Рассмотрим удар двух тел массами m 1 и m 2, скорости которых до удара V 1 и V 2 (рис. 8.1). Для неупругого удара можно применить только закон сохранения импульса, так как механическая энергия не сохраняется
. (8.1)
 |
Откуда скорость совместного движения равна
. Чтобы найти скорость шаров после удара, надо спроецировать уравнение (8.1) на выбранные оси координат и из уравнений определить проекции скорости U. Либо определить скорость U по векторной диаграмме, которая имеет вид треугольника, используя тригонометрические соотношения между сторонами треугольника.
Потери механической энергии при неупругом ударе превращаются во внутреннюю энергию тел, то есть в теплоту. Следовательно, теплоту можно определить как разность кинетических энергий до и после удара
. (8.2)
В технике явление неупругого удара применяют для двух целей. При ковке, штамповке деталей следует по возможности большую часть кинетической энергии молота массой m превратить в работу пластической деформации поковки. Для этого массу наковальни М делают как можно больше (рис. 8.2). Докажем это. По закону сохранения импульса для удара молота по наковальне 
определим скорость сотрясения наковальни U и затем энергию сотрясения 
. Тогда КПД 
тем больше, чем больше масса наковальни.
Наоборот, при забивании гвоздя молотком потери энергии на работу деформации должны меньше, а большая часть энергии молотка должна переходить в кинетическую энергию молотка с гвоздем после удара. Поэтому масса молотка должна быть больше массы гвоздя. Но так, чтобы гвоздь не согнулся.
Упругий удар
Для идеально упругого удара выполняются закон сохранения импульса и закон сохранения механической энергии. Рассмотрим идеально упругий центральный удар двух шаров, при котором скорости тел направлены по линии центров масс. Пусть начальные скорости направлены в одну сторону. Так как шары после удара отталкиваются друг от друга, то после удара они будут двигаться с неизвестными различными скоростями U 1 и U 2 по линии центров масс. Запишем закон сохранения импульса в проекции на направление движения первого шара и закон сохранения энергии
, (8.3)
. (8.4)
Имеем два уравнения с двумя неизвестными U 1и U 2. Чтобы решение выполнить более просто, заменим уравнение с квадратами скоростей (8.4) третьим уравнением, которое получим, после преобразования уравнений (8.4) и (8.5).
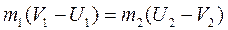, (8.5)
. (8.6)
После деления уравнений получим уравнение первой степени
. (8.7)
Решая совместно уравнения уже первого порядка (8.5) и (8.7), получим для скоростей тел после упругого удара формулы
, (8.8) 
. (8.9)
Рассмотрим частный случай, когда массы шаров равны: m 1 = m 2. Тогда скорости шаров после упругого удара будут равны 
. То есть, шары после удара обмениваются скоростями. А если второй шар до удара покоился, то после удара он будет двигаться со скоростью первого шара, а первый шар остановится.
При нецентральном ударе явление осложняется скольжением шаров в точке удара. Интересен случай упругого удара, при котором первый шар налетает на покоящийся второй шар равной массы, как в биллиарде. При ударе без трения энергия сохраняется. После сокращения на одинаковые массы уравнения законов сохранения импульса(8.3) и энергии (8.4) примут вид: 
и 
. Так как векторы первого уравнения образуют треугольник, то второе уравнение является теоремой Пифагора для этого треугольника. Следовательно, шары после удара разлетаются всегда под углом 90о.
Сцепление вагонов
Локомотив и вагоны сцепляются для совместного движения в поезд. Сцепление вагонов происходит с помощью автосцепок, без участия человека. Автосцепка предназначена для автоматического сцепления вагонов в состав, передачи тяговых продольных усилий при движении, смягчения сил удара между вагонами при сцепке и при движении. Автосцепка состоит из корпуса, в котором находится замок и поглощающий аппарат. Поглощающий аппарат имеет в составе пружину и гаситель колебаний. Пружина, сжимаясь при сцеплении, смягчает силу удара. В гасителе механическая энергия колебаний вагонов превращается в работу сил трения клина при скольжении по корпусу аппарата.
Сцепление вагонов происходит кратковременно. Поэтому ударные силы в автосцепках вагонов, согласно второму закону Ньютона 
, при Δ t → 0, достаточно велики. Так что можно пренебречь силой сопротивления при качении колес по рельсам на время удара. Таким образом, для процесса сцепления можно считать систему тел "вагоны" замкнутой и применить для решения задачи о сцеплении вагонов закон сохранения импульса.
Пусть вагон массы m со скоростью V накатывается на состав массы М, стоящий на горизонтальном участке. Пусть происходит сцепление (рис. 8.3). Если автосцепки состава в растянутом состоянии, то сначала накатывающий вагон сцепится с первым, потом они вместе толкнут второй, потом третий и так далее. По составу полетит перестук сжимающихся автосцепок. Если перестук затухнет, то состав со сжатыми автосцепками покатится с некоторой скоростью U. А может быть, последний вагон, получив некоторую скорость, откатываясь, потянет за собой предпоследний вагон, растягивая автосцепку. Перестук растягивающихся автосцепок полетит назад. И так до тех пор, пока энергия, которой предназначено потеряться, не превратится в работу против сил трения. В конце концов, состав с прицепленным вагоном как одно целое будет двигаться с той же самой скоростью U.
Определим эту скорость U после сцепления. Применим закон сохранения импульса в проекции на направление движения: импульс накатывающегося вагона до сцепления равен суммарному импульсу вагона с составом после сцепления
mV = (M+m) U (8.10)
Отсюда скорость движения состава после сцепления будет равна
. (8.11)
Совместное движение вагонов после сцепления является признаком неупругого удара. Как известно, при неупругом ударе тел кинетическая энергия не сохраняется. То же наблюдается и при сцеплении вагонов: часть кинетической энергии накатывающегося вагона, которой следует потеряться, превращается частично в энергию срабатывания автосцепок крайних вагонов и остальное в теплоту вследствие работы сил трения в поглощающих механизмах автосцепок и сил трения при качении колес по рельсам.
Потери Q кинетической энергии в процессе сцепления, которые должны быть, равны разности кинетических энергий вагона до сцепления и вагона с составом после сцепления
. (8.12)
Автосцепки крайних вагонов стоящего состава и накатывающего сцепа находятся в растянутом состоянии. Так что соударяются, прежде всего, крайние вагоны, как будто один на один. Уже потом взаимодействие передается другим вагонам. Энергия, теряемая в процессе сцепления, например, двух одинаковых вагонов, по формуле (8.12) равна половине кинетической энергии накатывающегося вагона. Эта потерянная кинетическая энергия является частью общих потерь (8.12) и расходуется на то, чтобы сжать пружины автосцепок обоих вагонов и на работу против сил трения в поглощающих аппаратах в процессе первого сжатия пружин
. (8.13)
Здесь х max – максимальная деформация пружин в процессе первого сжатия. Эта деформация должна быть достаточна для срабатывания замка автосцепки, но такая, чтобы витки пружины не коснулись друг друга. Зная работу сил трения 
, можно по уравнению (8.13) рассчитать деформацию пружин.
Задачи
1. На платформу массой 40 т поставили контейнер массой 20 т со скоростью 0,5 м/с. Определить наибольшую деформацию рессор вагона и смещение положения равновесия платформы. Коэффициент упругости рессор 2 106 Н/м.
2. В составе из шести одинаковых стоящих вагонов крайний вагон под действием пружин автосцепки оттолкнулся от остальных. Пружины были сжаты на 5см. Коэффициент упругости пружин 2·105 Н/м. Определить скорости вагонов после разъединения.
3. Вагон массой 60 т, двигаясь со скорость 1 м/с, сталкивается с пятью стоящими таким же вагонами. Определить скорость вагонов после сцепления и максимальную деформацию пружины автосцепки, если коэффициент упругости 2·105 Н/м.
4. Вагон массой 60 т, двигаясь со скоростью 1 м/с, сталкивается со стоящим вагоном массой 20 т. Определить, произойдет ли сцепление вагонов. Коэффициент упругости пружин автосцепки 2·105 Н/м. Сцепление происходит при деформации пружин не менее 5 см. Определить наибольшую силу удара и потери механической энергии.
5. На платформу массой 20 т, движущейся со скоростью 1м/с, высыпан песок массой 40 т за время 10 с. Определить зависимость скорости платформы от времени погрузки и мощность тепловыделения при трении песка о платформу.
6. По платформе массой 20 т начал движение танк массой 50 т со скоростью 1 м/с относительно платформы. Определить скорость движения платформы по рельсам.
7. С платформы массой 50 т был произведен выстрел снарядом массой 50 кг со скоростью 500 м/с вдоль рельсов. Определить скорость платформы после выстрела и теплоту сгорания пороха, если КПД пушки 20%. Трением пренебречь. Определить скорость снаряда, если платформа была бы заторможена.
9. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Вращательным движением твердого тела относительно оси является движение, при котором траектории точек тела являются концентрическими окружностями, центры которых находятся на линии, являющейся осью вращения.
