Момент инерции материальной точки равен произведению квадрата расстояния от точки до оси вращения, mR 2. Момент инерции твердых тел равен сумме моментов инерции материальных точек, из которых состоит тело, то есть интегралу от произведения квадрата расстояния элементарных частиц тела от оси на величину их массы:
. (9.10)
Произведем расчет момента инерции тел простой формы.
1.Кольцо
Все частицы кольца находятся на одинаковом расстоянии от оси (рис. 9.3). Вынесем в формуле момента инерции (9.10) расстояние r = R за знак интеграла, а интеграл от элементарных масс дает полную массу кольца. Итак, 
.
2. Диск
 |
Пусть масса диска m, радиус R. Разделим диск на тонкостенные кольца. Несмотря на большие размеры колец, масса их будет ничтожно мала, если толщина стенки будет много меньше радиуса. Масса элементарного кольца пропорциональна площади торца кольца:
. Аналогично, масса диска пропорциональна площади торца: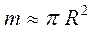 
. Из пропорций получим: 
. Подставим массу элементарного кольца под знак интеграла момента инерции 
. Нижний предел интегрирования равен радиусу элементарного кольца в центре диска r = 0, верхний предел равен радиусу кольца у поверхности диска r = R. Интегрируя, получим формулу момента инерции диска относительно оси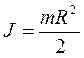 
.
3. Стержень
Пусть масса стержня m равномерно распределена по длине стержня l с линейной плотностью 
. Ось вращения проходит через середину, перпендикулярно стержню. Разделим стержень на элементарные отрезки длиной dr с массой 
. Подставим массу элементарного отрезка в интеграл момента инерции 
. Интегрируя, получим формулу момента инерции стержня 
.
Задачи
1. Уравнение зависимости угла поворота якоря тягового двигателя от времени имеет вид 
. Передаточное отношение редуктора 4,2, диаметр колеса 1,18 м. Определить зависимость скорости и ускорения поезда от времени.
2. Локомотив движется с ускорением 0,1 м/с2. Определить угловое ускорение якоря тягового двигателя. Передаточное отношение редуктора 4,2, диаметр колеса 1,18 м.
3. Момент электромагнитных сил, действующих на якорь тягового двигателя, установленного на стенде, равен 400 Н·м. С каким угловым ускорением вращается якорь? Якорь считать цилиндром радиусом 0,25 м и массой 500 кг.
4. На шкив тягового двигателя, установленного на стенде, надет приводной ремень. Силы натяжения ветвей ремня равны 100 Н и 200 Н. Определить момент сил и мощность двигателя при частоте вращения 1200 об/мин, если диаметр шкива 0,20 м.
5. При трогаии поезда одна колесная пара буксовала в течении 3 с и достигла скорости вращения 3 об/с. Определить момент сил, действующих на колесо со стороны электродвигателя. Коэффициент трения скольжения 0,15, сила давления колеса на рельс 100 кН, момент инерции колесной пары 500 кг м2.
6. Колесная пара на кг·м2стенде приводится во вращение электродвигателем с угловым ускорением 0,04 1/с2. Определить вращающий момент сил якоря электродвигателя, если момент инерции колесной пары 500 кг·м2, момент инерции якоря 100 кг·м2. Передаточное отношение зубчатой передачи 4,5 (рис. 9.4).
7. Колесная пара, с моментом инерции 600 кг·м2 на стенде вращается с угловой скоростью 100 1/с. Определить угловое ускорение под действием сил трения тормозных колодок, прижатых с силой 500 Н. Коэффициент трения скольжения 0,18. Определить число оборотов до остановки.
10. ДИНАМИКА ПЛОСКОГО ДВИЖЕНИЯ ТЕЛ
Плоскимявляется движение, при котором траектории точек тела лежат в параллельных плоскостях.
1. Движение центра масс
Центр масс твердого тела это точка, к которой приложена результирующая сила инерции при поступательном движении неинерциальной системы отсчета. В этом случае силы инерции, действующие на тела (или части тела), являются параллельными силами. Точно также параллельны в однородном поле тяжести силы тяжести, действующие на частицы тела. В этом случае положение центра масс и положение центра тяжести тела совпадают.
Выведем формулу радиус-вектора центра тяжести. Потребуем, чтобы момент результирующей силы тяжести относительно некоторой оси y был бы равен векторной сумме моментов сил тяжести всех частиц тела относительно этой же оси 
(рис. 10.1).
Отсюда радиус-вектор центра тяжести или центра масс относительно выбранной оси можно определить по формуле
. (10.1)
Здесь m – суммарная масса тел.Проецируя это равенство на оси координат, можно определить три координаты центра масс.
Перенесем массу тела в левую часть уравнения и дважды продифференцируем по времени. Вторая производная это ускорение. В результате получим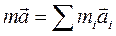 
. Произведение массы частицы на её ускорение равно действующей на частицу силе, а их сумма равна равнодействующей силе. Таким образом, центр масс твердого тела движется как материальная точка, в которой сосредоточена масса тела, к которой приложены все внешние силы,
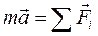. (10.2)
Отсюда следует, что если тело движется поступательно, то его можно принимать за материальную точку.
