Рассмотрим скатывание вагона с общей массой кузова и колесных пар m по рельсам, расположенным под углом α к горизонту (рис. 10.4). Учтем в решении задачи вращательное движение колесных пар. Представим качение колеса как сумму двух движений: поступательного движения, которое объединим с движением вагона, и вращательного движения относительно оси колесной пары. Пусть суммарный момент инерции всех колесных пар вагона равен J, радиус круга катания – R.
На все колесные пары действуют следующие силы: суммарная сила тяжести mg кузова и колесных пар, силы нормального давления рельсов N и сила сопротивления Fсопр со стороны рельсов. Обе эти силы приложены в зоне контакта колес с рельсами. Еще в зоне контакта действует сила сцепления колес с рельсами Fсц. По природе это сила трения покоя, она направлена вдоль рельса так, чтобы исключить проскальзывание колеса по рельсу. В данном случае сила сцепления направлена против хода вагона, чтобы ее момент сил создал ускоренное вращение колеса по часовой стрелке.
Запишем уравнение динамики поступательного движения вагона совместно с поступательным движением колесных пар: 
. Спроецируем уравнение на оси координат
Ox: ma = mg sin α – Fcц – Fсопр, (10.8)
Oy: 0 = N – mg cos α. (10.9)
По закону трения, сила сопротивления пропорциональна силе нормального давления, которая, в свою очередь (по уравнению 10.9), равна проекции силы тяжести на ось Oy Fсопр= μсопрmg cos α. Существующие уклоны железнодорожных путей невелики, и косинус угла таких уклонов можно принять равным единице.Также обозначим для краткости записи уклон одной буквой sin α = i.
Запишем уравнение динамики вращательного движения всех колесных пар вагона относительно их осей (рис. 10.4,б): произведение момента инерции всех колесных пар вагона J на угловое ускорение ε равно моменту сил сцепления относительно осей колесных пар:
J ε = Fcц R (10.10)
Моменты силы сопротивления и силы давления рельсов N не входят в уравнение.Это связано с тем, что их равнодействующая проходит через ось колесной пары и не создает результирующего вращающего момента сил. Не создает вращающего момента сила тяжести вагона, приложенная к осям колесных пар.
Угловое ускорение связано с ускорением поступательного вагона соотношением ε = a/R. Переписав уравнение (10.10) в виде 
, получим вместе с (10.8) два уравнения с двумя неизвестными: ускорением и силой сцепления. Сначала сложим эти уравнения для исключения силы сцепления
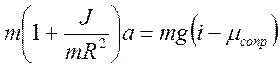, (10.11)
и получим для ускоренияпри скатывании вагона формулу
. (10.12)
Если бы инертностью вращения колес можно было пренебречь (J = 0), то ускорение было бы больше: a = g (i – μсопр). То есть инерция вращения колес увеличивает общую инертность вагона. Коэффициент в знаменателе формулы 
учитывает вклад в общую инертность вагона инертность вращения колес, а для локомотива еще учитывается еще инертность якорей электродвигателей.
Формально при решении таких задач можно не применять уравнение динамики вращательного движения колес. Достаточно одного уравнения (10.11), в котором вместо инертной массы подставить так называемую эффективную массу, равную произведению массы на коэффициент инертности колес mэфф= mγ. А массу, определяющую силу тяжести, оставить без изменения. Именно так поступают при производстве тяговых расчетов. Поправочный коэффициент невелик: 1,05 для груженого вагона, для порожнего вагона роль колес в инертности больше – 1,10, и для электровоза – 1,30.
Определим скорость вагона в конце спуска длиной S. При равноускоренном движении между путем, скоростью и ускорением существует кинематическое соотношение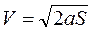 
. Подставив формулу рассчитанного ускорения (10.10), получим для скорости вагона в конце спуска формулу
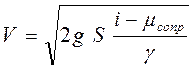. (10.13)
Как и следовало ожидать, при погрузке роль инертности вращения колёс уменьшается и поэтому груженые вагоны скатываются быстрее, чем порожние.
Задачи
1. Определить, во сколько раз эффективная масса больше тяготеющей массы поезда массой 4000 т, если масса колес составляет 15% от массы поезда. Колеса считать дисками диаметром 1,02 м. Как изменится ответ, если диаметр колес будет в два раза меньше?
2.Определить ускорение, с которым скатывается колесная пара массой 1200 кг с горки с уклоном 0,08. Колеса считать дисками. Коэффициент сопротивления качению 0,004. Определить силу сцепления колес с рельсами.
3. Определить, с каким ускорением закатывается колесная пара массой 1400 кг на горку с уклоном 0,05. Коэффициент сопротивления 0,002. Каким должен быть коэффициент сцепления, чтобы колеса не буксовали. Колеса считать дисками.
4. Определить, с каким ускорением скатывается вагон массой 40 т, с горки с уклоном 0,020, если у него восемь колес массой 1200 кг и диаметром 1,02 м. Определить силу сцепления колес с рельсами. Коэффициент сопротивления 0,003.
5. Определить силу давления тормозных колодок на бандажи, если поезд массой 4000 т тормозит с ускорением 0,3 м/с2. Момент инерции одной колесной пары 600 кг·м2, количество осей 400, коэффициент трения скольжения колодки 0,18, коэффициент сопротивления качению 0,004.
6. Определить силу торможения, действующую на четырехосный вагон массой 60 т на тормозной площадке сортировочной горки, если скорость на пути 30 м уменьшилась от 2 м/с до 1,5 м/с. Момент инерции одной колесной пары 500 кг·м2.
7. Скоростемер локомотива показал увеличение скорости поезда в течении одной минуты от 10 м/с до 60 м/c. Вероятно, произошло буксование ведущей колесной пары. Определить момент сил, действующих на якорь электродвигателя. Момент инерции колесной пары 600 кг·м2, якоря 120 кг·м2. Передаточное отношение зубчатой передачи 4,2. Сила давления на рельсы 200 кН, коэффициент трения скольжения колес по рельсу 0,10.
11. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАТЕЛЬОГО
ДВИЖЕНИЯ
