Даны схема механизма (рисунок 5 а) и следующие исходные данные:
sr = OM = 5(1 + cos(2p t)), см; φ e = 2 t + 3 t 2, рад; t 1 = 1/3 с.
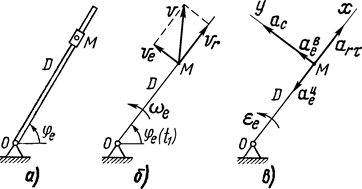
Рисунок 5 – Схема механизма (а) и схемы для определения абсолютной скорости (б)
и ускорения (в)
Решение.
1. Определение положения точки М на теле D в момент t 1. Относительное движение точки М по телу D определяется дуговой координатой sr = OM. В момент времени t 1 = 1/3 с
sr = OM = 5(1 + cos(2p/3)) = 5(1 – 0,5) = 2,5 см.
Положение тела D определяется угловой координатой φ e. В момент t 1
φ e = 2/3+ 3(1/3)2 = 1рад.
Положение тела и точки на нем в момент времени t 1 показано на рисунке 5 б.
2. Определение абсолютной скорости точки М. Абсолютная скорость точки определяется как геометрическая сумма относительной и переносной скоростей:  .
.
Модуль относительной скорости равен  , де
, де  .
.
В момент времени t 1:  см/с;
см/с;  см/с.
см/с.
Положительный знак алгебраической величины  показывает, что вектор относительной скорости
показывает, что вектор относительной скорости  направлен в сторону возрастания sr.
направлен в сторону возрастания sr.
Модуль переносной скорости равен  , где w e – модуль угловой скорости тела в его переносном вращении;
, где w e – модуль угловой скорости тела в его переносном вращении;
 ;
; 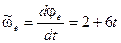 .
.
В момент времени t 1  рад/с;
рад/с;  рад/с.
рад/с.
Положительный знак алгебраической величины  показывает, что вращение тела D происходит в направлении отсчета угловой координаты φ e (рисунок 5 б). Вектор
показывает, что вращение тела D происходит в направлении отсчета угловой координаты φ e (рисунок 5 б). Вектор  направлен по оси, проходящей через точку О и нормальной плоскости вращения. Поэтому на рисунке 5 б вектор
направлен по оси, проходящей через точку О и нормальной плоскости вращения. Поэтому на рисунке 5 б вектор  , направленный на наблюдателя, проецируется в точку.
, направленный на наблюдателя, проецируется в точку.
Теперь можно определить модуль переносной скорости:
 см/с.
см/с.
Вектор переносной скорости  направлен из точки М перпендикулярно ОМ в направлении вращения тела D (согласно
направлен из точки М перпендикулярно ОМ в направлении вращения тела D (согласно  ).
).
Так как векторы  и
и  взаимно перпендикулярны, то модуль абсолютной скорости точки М можно определить как
взаимно перпендикулярны, то модуль абсолютной скорости точки М можно определить как
 см/с.
см/с.
Направление вектора абсолютной скорости 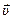 показано на рисунке 5 б.
показано на рисунке 5 б.
3. Определение абсолютного ускорения точки М. Абсолютное ускорение точки при сложном движении равно геометрической сумме относительного, переносного и кориолисова ускорений:
 или
или  ,
,
где 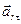 ,
,  – касательная и нормальная составляющие относительного ускорения;
– касательная и нормальная составляющие относительного ускорения;
 – вращательная и центростремительная составляющие переносного ускорения.
– вращательная и центростремительная составляющие переносного ускорения.
Модуль относительного касательного ускорения равен
 , где
, где 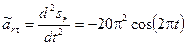 .
.
В момент времени t 1:  см/с2,
см/с2,  см/с2. Положительный знак
см/с2. Положительный знак  показывает, что вектор
показывает, что вектор 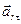 направлен в сторону возрастания дуговой координаты sr. А так как знаки
направлен в сторону возрастания дуговой координаты sr. А так как знаки  и
и  одинаковы, то относительное движение точки М ускоренное (рисунок 5 в).
одинаковы, то относительное движение точки М ускоренное (рисунок 5 в).
Модуль относительного нормального ускорения 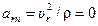 , так как траекторией относительного движения является прямая и радиус ее кривизны r = 0.
, так как траекторией относительного движения является прямая и радиус ее кривизны r = 0.
Модуль переносного вращательного ускорения:
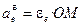 , где
, где  – модуль углового ускорения тела в его переносном движении:
– модуль углового ускорения тела в его переносном движении:  рад/с2.
рад/с2.
Так как знаки алгебраических величин  и
и  одинаковы и
одинаковы и  , то вращение тела D равноускоренное. Вектор
, то вращение тела D равноускоренное. Вектор  направлен так же, как и
направлен так же, как и  . Тогда
. Тогда 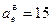 см/с2.
см/с2.
Вектор  направлен так же, как и
направлен так же, как и  (рисунок 5 в).
(рисунок 5 в).
Модуль переносного центростремительного ускорения:
 см/с2.
см/с2.
Вектор  направлен к центру вращения, к точке О.
направлен к центру вращения, к точке О.
Кориолисово ускорение по определению равно
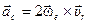 , а его модуль равен
, а его модуль равен  .
.
В данном случае  и
и  . С учетом этого
. С учетом этого  см/с2.
см/с2.
Расположение и направление вектора  соответствует определению векторного произведения векторов (см. рисунок 5 в). Вектор
соответствует определению векторного произведения векторов (см. рисунок 5 в). Вектор  расположен перпендикулярно плоскости, проходящей через векторы сомножители, и направлен в ту сторону, откуда виден поворот (на меньший угол) первого сомножителя ко второму против вращения часовой стрелки.
расположен перпендикулярно плоскости, проходящей через векторы сомножители, и направлен в ту сторону, откуда виден поворот (на меньший угол) первого сомножителя ко второму против вращения часовой стрелки.
Модуль абсолютного ускорения точки найдем способом проекций. Для этого проведем координатные оси x и y (см. рисунок 5 в) и спроецируем на них составляющие вектора ускорения:
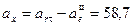 см/с2;
см/с2;  см/с2.
см/с2.
Тогда  см/с2.
см/с2.
Динамика
Задание Д.1. Вторая (обратная) задача динамики материальной точки
Варианты 1–5 (таблица 9, схема 1). Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол а с горизонтом, в течение t с. Его начальная скорость vA. Коэффициент трения скольжения тела по плоскости равен f.
В точке В тело покидает плоскость со скоростью vB ипопадает со скоростью vc в точку С плоскости BD, наклоненной под углом βк горизонту, находясь в воздухе T с.
При решении задачи тело принять за материальную точку; сопротивление воздуха не учитывать.
Вариант 1. Дано: a= 30°; vA = 0 м/с; f = 0,2; l =10 м; β = 60°. Определить t и h.
Вариант 2. Дано: a= 15°; vA = 2 м/с; f = 0,2; h = 4 м; β = 45°. Определить l и уравнение траектории точки на участке ВС.
Вариант 3. Дано: a= 30°; vA = 2,5 м/с; f ≠ 0; l = 8м; d = 10 м; β= 60°. Определить vB и t.
Вариант 4. Дано: vA = 0; t = 2 с; l = 9,8м; β = 60°; f = 0. Определить a и T.
Вариант 5. Дано: a = 30°; vA = 0; l = 9,8 м; t = 3 с; β = 45°. Определить f и vС.
Варианты 6–10 (таблица 9, схема 2). Лыжник подходит к точке А участка трамплина АВ, наклоненного под углом а к горизонту и имеющего длину l, со скоростью vA. Коэффициент трения скольжения лыж на участке АВ равен f. Лыжник от А до В движется t с; в точке В со скоростью vB он покидает трамплин. Через Т с лыжник приземляется со скоростью vС в точке С горы, составляющей угол βс горизонтом.
При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха.
Вариант 6. Дано: a = 20°; f = 0,1; t = 0,2 с; h = 40 м; β = 30°. Определить l и Vc.
Вариант 7. Дано: a= 15°; f =0,1; vA = 16м/с; l = 5 м; β = 45°. Определить vB и Т.
Вариант 8. Дано: vA = 21 м/с; f = 0; t = 0,3 с; vB = 20 м/с; β = 60°. Определить а и d.
Вариант 9. Дано: a = 15°; t = 0,3 с; f =0,1; h =  м; β = 45°. Определить vB и vA.
м; β = 45°. Определить vB и vA.
Вариант 10. Дано: a=15°; f =0; vA= 12м/с; d = 50 м; β = 60°. Определить tи уравнение траектории лыжника на участке ВС.
Варианты 11–15 (таблица 9, схема 3). Имея в точке А скорость vA,мотоцикл поднимается t с по участку АВ длиной l, составляющему с горизонтом угол a. При постоянной на всем участке АВ движущей силе Р мотоцикл в точке В приобретает скорость vB и перелетает через ров шириной d, находясь в воздухе T с и приземляясь в точке С со скоростью vС. Масса мотоцикла с мотоциклистом равна т.
При решении задачи считать мотоцикл с мотоциклистом материальной точкой и не учитывать силы сопротивления движению.
Вариант 11. Дано: a = 30°; Р ≠0; l = 40 м; vA = 0: vB = 4,5 м/с; d = 3 м;Определить t и h.
Вариант 12. Дано: a = 30°; Р = 0; l = 40 м; vB = 4,5 м/с; h = 1,5 м. Определить vA и d.
Вариант 13. Дано: a = 30°; т = 400 кг; vA = 0; t = 20 с; d = 3 м; h = 1,5 м. Определить Р и l.
Вариант 14. Дано: a = 30°; т = 400 кг; Р = 2,2 кН; vA = 0; l = 40 м; d = 5м. Определить vB и vС.
Вариант 15. Дано: a = 30°; vA = 0; Р = 2кН; l = 50 м; h = 2 м; d = 4 м. Определить Т и т.
Варианты 16–20 (таблица 9, схема 4). Камень скользит в течение tс по участку АВ откоса, составляющему угол a с горизонтом и имеющему длину l. Его начальная скорость vA. Коэффициент трения скольжения камня по откосу равен f. Имея в точке В скорость vB, камень через Т с ударяется в точке С о вертикальную защитную стену. При решении задачи принять камень за материальную точку; сопротивление воздуха не учитывать.
Вариант 16. Дано: a = 30°; vA = 1 м/с; l = 3 м; f = 0,2; d = 2,5 м. Определить h и Т.
Вариант 17. Дано: a= 45°; l = 6 м; vB = 2·vA; t = 1 с; h = 6 м. Определить d и f.
Вариант 18. Дано: a = 30°; l= 2 м; vA = 0; f = 0,1; d = 3 м. Определить h и t.
Вариант 19. Дано: a = 15°; l = 3 м; vB = 3 м/с, f ≠0; t= 1,5 с; d = 2 м. Определить vA и h.
Вариант 20. Дано: a = 45°; vA = 0; f = 0,3; d = 2 м; h = 4 м. Определить l и t.
Варианты 21–25 (таблица 9, схема 5). Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол a с горизонтом. Его начальная скорость vA. Коэффициент трения скольжения равен f. Через t с тело в точке В со скоростью vB покидает наклонную плоскость и падает на горизонтальную плоскость в точку С со скоростью vС;приэтом оно находится в воздухе Т с.
При решении задачи принять тело за материальную точку и не учитывать силы сопротивления движению.
Вариант 21. Дано: a= 30°; f = 0,1; vA = 1 м/с; t = 1,5 с; h = 10 м. Определить vB и d.
Вариант 22. Дано: vA = 0; a = 45°; l =10 м; t = 2 с. Определить f и уравнение траектории на участке ВС.
Вариант 23. Дано: f =0; vA = 0; l = 9,81 м; t = 2с; h = 20 м. Определить aи Т.
Вариант 24. Дано: vA =0; a=30°; f =0,2; l = 10 м; d = 12 м. Определить t и h.
Вариант 25. Дано: vA = 0; a = 30°; f = 0,2; l =6 м; h= 4,5 м. Определить t и vС.
Варианты 26–30 (таблица 9, схема 6). Имея в точке А скорость vA, тело движется по горизонтальному участку АВ длиной l в течение t с. Коэффициент трения скольжения тела по плоскости равен f. Со скоростью vB тело в точке В покидает плоскость и попадает в точкуС со скоростью vС, находясь в воздухе Т с. При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.
Вариант 26. Дано: vA = 7 м/с; f = 0,2; l = 8 м; h = 20 м. Определить d и vС .
Вариант 27. Дано: vA = 4 м/с; f = 0,1; t = 2 с; d = 2 м. Определить vB и h.
Вариант 28. Дано: vB = 3 м/с; f =0,3; l = 3 м; h = 5 м. Определить vA и Т.
Вариант 29. Дано: vA = 3 м/с; vB = 1 м/с; l = 2,5 м; h = 20 м. Определить f и d.
Вариант 30. Дано: f =0,25; l =4 м; d = 3 м; h = 5 м. Определить vA и t.
Таблица 9 – Рисунки к заданию Д.1

Пример 1 выполнения задания (рисунок 6).
При строительстве железных дорог для защиты кюветов от попадания в них каменных осыпей устраивается «полка» DC. Учитывая возможность движения камня из наивысшей точки А откоса и полагая при этом его начальную скорость vA = 0, определить наименьшую ширину полки b и скорость vC, с которой камень падает на нее. По участку АВ откоса длиной l под углом a к горизонту камень движется t с.

Рисунок 6 – Рисунок к примеру 1 задания Д.1
При решении задачи считать коэффициент f трения скольжения камня на участке АВ постоянным, а сопротивлением воздуха пренебречь.
Дано: vA =0; a = 60°; l = 4 м; t = 1 с; f ≠ 0; h = 5 м; β = 75 °.
Определить b и vC.
Решение.
Рассмотрим движение камня на участке АВ. Принимая камень за материальную точку, отобразим (рисунок 7) действующие на него силы: вес  ,нормальную реакцию
,нормальную реакцию 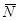 и силу
и силу  трения скольжения. Запишем дифференциальное уравнение прямолинейного движения несвободной материальной точки на участке АВ, обозначив x 1 через x:
трения скольжения. Запишем дифференциальное уравнение прямолинейного движения несвободной материальной точки на участке АВ, обозначив x 1 через x:
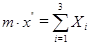 .
.

Рисунок 7 – Расчетная схема: участок АВ – а), участок BC – б)
Проекция  ускорения
ускорения  на ось Ax 1 по определению равна:
на ось Ax 1 по определению равна: 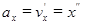 . Тогда
. Тогда  .
.
Отсюда с учетом  :
:

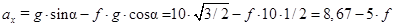 . (7)
. (7)
Так как f < 1,то проекция  ускорения
ускорения  на ось Ax1 положительна и постоянна, т. е.
на ось Ax1 положительна и постоянна, т. е.  (при этом
(при этом  ), то прямолинейное движение на участке AB – равноускоренное.
), то прямолинейное движение на участке AB – равноускоренное.
Запишем, зная, что по определению  , уравнение (7) в дифференциальной форме
, уравнение (7) в дифференциальной форме  .
.
Разделяя переменные интегрирования, получим
 .
.
Интегрируя  правую и левую части уравнения совместно, получим
правую и левую части уравнения совместно, получим  .
.
Константу C 1интегрирования найдем по начальным условиям, зная, что в момент начала движения:
 ,
, 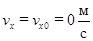 ,
, 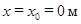 . (НУ AB)
. (НУ AB)
 . Откуда
. Откуда  .
.
Физический смысл константы:  – проекция начальной скорости точки на ось Ax. Тогда
– проекция начальной скорости точки на ось Ax. Тогда
 . (8)
. (8)
Запишем, зная, что по определению  , уравнение (8) в дифференциальной форме:
, уравнение (8) в дифференциальной форме:  . Разделяя переменные интегрирования, получим
. Разделяя переменные интегрирования, получим  .
.
Интегрируя 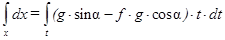 правую и левую части уравнения совместно, получим
правую и левую части уравнения совместно, получим  .
.
Константу  интегрирования найдем по начальным условиям (НУAB).
интегрирования найдем по начальным условиям (НУAB).
 . Откуда
. Откуда 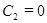 .
.
Физический смысл константы:  м – начальная абсцисса точки.
м – начальная абсцисса точки.
Тогда
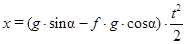 . (9)
. (9)
Совокупность уравнений (7)–(9) – уравнения прямолинейного равноускоренного движения несвободной материальной точки на участке AB. Положив  ,
,  ,
, 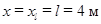 в уравнениях (8) и (9), получим:
в уравнениях (8) и (9), получим:
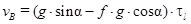 ,
, 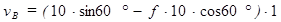 (8*)
(8*)
 ,
,  (9*)
(9*)
и определим: f, vВ.
Из уравнения (9*) найдем:
 .
.
Решая уравнение (8*), получим:
 .
.
Участок движения BC.
Для движения свободной материальной точки на участке BC запишем основное уравнение  динамики в проекциях на оси Bx и By в дифференциальной форме в общем виде:
динамики в проекциях на оси Bx и By в дифференциальной форме в общем виде:
 ,
,
 .
.
По определению 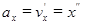 ,
,  . Тогда:
. Тогда:  ,
,  ,
,
 (10)
(10)
Так как ax= 0 – const, ay= g – const,тодвижение:
– по горизонтали на всем участке BC – равномерное,
– по вертикали – на всем участке BC равнопеременное – равноускоренное.
Мгновенное, истинное, полное ускорение материальной точки равно:
 (10*)
(10*)
Так как ускорение  постоянно и по величине, и по направлению, а угол между касательной m t к траектории и ускорением
постоянно и по величине, и по направлению, а угол между касательной m t к траектории и ускорением  переменный, то проекция at ускорения на касательную переменна по величине
переменный, то проекция at ускорения на касательную переменна по величине 
Поэтому движение материальной точки по кривой BC не есть равнопеременное. На участке BC движение – ускоренное (at >0 – var.).
Запишем, зная, что по определению  ,
,  , уравнения (10) в дифференциальной форме:
, уравнения (10) в дифференциальной форме:
 ,
,
 .
.
Разделяя переменные интегрирования, получим:  ,
,  .
.
Интегрируя  ,
,  правую и левую части уравнений совместно, получим:
правую и левую части уравнений совместно, получим:  ,
, 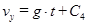 .
.
Константы C 3и C 4 интегрирования найдем по начальным условиям, зная, что в момент начала движения 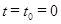 с,
с,  м,
м,  м,
м,
 ,
,  (НУ BC)
(НУ BC)
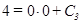 ,
,  .
.
Откуда  ,
, 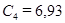 . Физический смысл констант интегрирования:
. Физический смысл констант интегрирования:  ,
,  – проекции начальной скорости на оси Bx и By. Тогда
– проекции начальной скорости на оси Bx и By. Тогда
 (11)
(11)
 (12)
(12)
Запишем, зная, что по определению  ,
,  , уравнения (11) и (12) в дифференциальной форме:
, уравнения (11) и (12) в дифференциальной форме:
 ,
,
 .
.
Разделяя переменные интегрирования, получим:  ,
,  .
.
Интегрируя  ,
,  правую и левую части уравнений совместно, получим:
правую и левую части уравнений совместно, получим:  ,
, 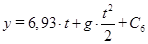 .
.
Константы 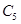 и
и  интегрирования найдем по начальным условиям (НУ BC):
интегрирования найдем по начальным условиям (НУ BC):  ,
,  . Откуда
. Откуда  ,
, 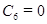 . Физический смысл констант интегрирования:
. Физический смысл констант интегрирования:  м,
м,  м – начальные координаты материальной точки. Тогда:
м – начальные координаты материальной точки. Тогда:
 (13)
(13)
 (14)
(14)
Совокупность уравнений (11)–(14) – уравнения движения свободной материальной точки на участке BC.
Положив  ? c,
? c,  ? м/с,
? м/с, 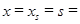 ? м,
? м,  5 м
5 м
в уравнениях (12)–(14), получим:
 , (12*)
, (12*)
 , (13*)
, (13*)
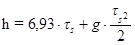 (14*)
(14*)
и определим: s, ts, vC.
Из уравнения (14*) найдем:
 с.
с.
Решая уравнения (12*) и (13*), получим:  м/с,
м/с,  м.
м.
Тогда наименьшая ширина полки равна:
 м.
м.
Скорость  падения материальной точки на землю равна:
падения материальной точки на землю равна:
 м/с.
м/с.
Пример 2 выполнения задания (рисунок 8).
Стопятидесятидвухмиллиметровая артиллерийская система посылает семидесятивосьмикилограммовый снаряд в цель.
Длина ствола 4 м. Угол наклона ствола к горизонту 45°. Давление пороховых газов в канале ствола 500 МПа. Сопротивление движению снаряда в канале ствола учтено, как трение скольжения (коэффициент трения скольжения равен 0,05).
Определить время движения снаряда в канале ствола и скорость движения снаряда на выходе из ствола.
Определить дальность,продолжительность, наибольшую высоту полета и скорость падения снаряда в цель, а также время подъема снаряда на наибольшую высоту.
Считать силы, действующие на снаряд постоянными, и не учитыватьсопротивление движению снаряда в воздухе.

Рисунок 8 – Рисунок к примеру 2
Дано: m =78 кг; l =4 м; a=45°; d =152 мм; p =500 МПа; f =0,05. Определить: t l, vВ, s, ts, h, vC, t h
Решение.
Сила  давления пороховых газов на снаряд (движущая сила) по величине равна произведению давления
давления пороховых газов на снаряд (движущая сила) по величине равна произведению давления 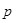 газов на площадь поперечного сечения снаряда (канала ствола) диаметром
газов на площадь поперечного сечения снаряда (канала ствола) диаметром  :
:
 Н.
Н.
Далее решим задачу, не принимая во внимание размеры и форму снаряда (твердого тела) и рассматривая его как материальную точку массой m.
Построим расчетную схему (рисунок 9). Отметим на схеме текущее положение материальной точки на участке AB и на участке BC, построим скорость  и ускорение
и ускорение 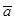 точки и действующие на нее силы.
точки и действующие на нее силы.
Движение несвободной материальной точки на прямолинейном участке AB обусловлено действием сил:  . На криволинейном участке BDC свободная материальная точка движется по горизонтали по инерции; по вертикали – снизу вверх по инерции, преодолевая действие силы
. На криволинейном участке BDC свободная материальная точка движется по горизонтали по инерции; по вертикали – снизу вверх по инерции, преодолевая действие силы  тяжести на участке BD, и только под действием силы
тяжести на участке BD, и только под действием силы  тяжести сверху вниз на участке DC.
тяжести сверху вниз на участке DC.
Участок движения AB. Запишем основное уравнение динамики (закон пропорциональности силы и ускорения в проекции на ось Ax) в дифференциальной форме в общем виде:  .
.
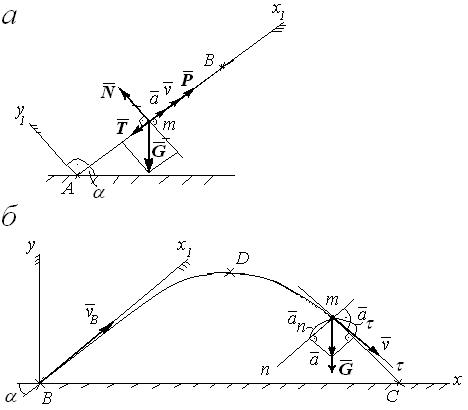
Рисунок 9 – Расчетная схема: для участка AB – a); для участка BДC – б)
Проекция  ускорения на ось Ax по определению равна:
ускорения на ось Ax по определению равна: 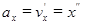 . Тогда
. Тогда  .
.
Отсюда с учетом  ,
, 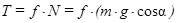 :
:
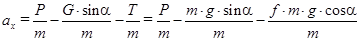 ,
,
 , (15)
, (15)
 . (15*)
. (15*)
Так как проекция ускорения на ось Ax постоянна  (при этом
(при этом  ), то прямолинейное движение на участке AB – равноускоренное.
), то прямолинейное движение на участке AB – равноускоренное.
Запишем, зная, что по определению  , уравнение (15) в дифференциальной форме
, уравнение (15) в дифференциальной форме
 .
.
Разделяя переменные интегрирования, получим:
 .
.
Интегрируя  правую и левую части уравнения совместно, получим
правую и левую части уравнения совместно, получим  .
.
Константу C 1интегрирования найдем по начальным условиям, зная, что в момент начала движения:
 ,
,  ,
,  , (НУ AB)
, (НУ AB)
 . Откуда
. Откуда  . Физический смысл константы:
. Физический смысл константы:  – проекция начальной скорости точки на ось Ax. Тогда
– проекция начальной скорости точки на ось Ax. Тогда
 . (16)
. (16)
Запишем, зная, что по определению  , уравнение (16) в дифференциальной форме:
, уравнение (16) в дифференциальной форме: 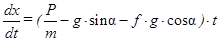 . Разделяя переменные интегрирования, получим
. Разделяя переменные интегрирования, получим  .
.
Интегрируя  правую и левую части уравнения совместно, получим
правую и левую части уравнения совместно, получим  .
.
Константу  интегрирования найдем по начальным условиям (НУ AB).
интегрирования найдем по начальным условиям (НУ AB).
 . Откуда
. Откуда 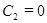 . Физический смысл константы:
. Физический смысл константы:  – начальная абсцисса точки. Тогда
– начальная абсцисса точки. Тогда
 . (17)
. (17)
Совокупность уравнений (15)–(17) – уравнения прямолинейного равноускоренного движения несвободной материальной точки на участке AB.
Положив  ,
, 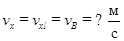 ,
, 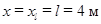 в уравнениях (16) и (17), получим:
в уравнениях (16) и (17), получим:
 , (16*)
, (16*)
 (17*)
(17*)
и определим: t, vВ.
Из уравнения (17*) найдем
 .
.
Решая уравнение (2*), получим:

=957 м/с.
Участок движения BDC. Для движения свободной материальной точки на участке BDC запишем основное уравнение динамики в проекциях на оси Bx и By в дифференциальной форме в общем виде:
 ,
,
 .
.
По определению 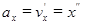 ,
,  . Тогда:
. Тогда:  ,
,  ,
,
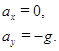 (18)
(18)
Так как ax= 0 – const, ay= -g – const, тодвижение:
– по горизонтали на всем участке BDC – равномерное;
– по вертикали – на всем участке BDC равнопеременное (на участке BD – равнозамедленное, на участке DC – равноускоренное).
Истинное, полное ускорение материальной точки равно:
 , м/с2 – const. (18*)
, м/с2 – const. (18*)
Внимание: направления стрелок у символов векторов  и
и  (орта оси ординат и ускорения свободного падения) разные.
(орта оси ординат и ускорения свободного падения) разные.
Так как ускорение  , м/с2, – постоянно и по величине, и по направлению, а угол между касательной mt к траектории и ускорением
, м/с2, – постоянно и по величине, и по направлению, а угол между касательной mt к траектории и ускорением  переменный, то проекция at ускорения на касательную переменна и по величине, и по знаку, т. е.
переменный, то проекция at ускорения на касательную переменна и по величине, и по знаку, т. е. 
Поэтому движение материальной точки по кривой BDC не есть равнопеременное. На участке BD – движение замедленное (at<0 – var.), на участке DC – ускоренное (at>0 – var.). В наивысшем положении D движение материальной точки – равномерное (локальное, на мгновение равномерное a t D=0).
Запишем, зная, что по определению  ,
,  , уравнения (18) в дифференциальной форме:
, уравнения (18) в дифференциальной форме:
 ,
,
 .
.
Разделяя переменные интегрирования, получим:  ,
,  .
.
Интегрируя  ,
,  правую и левую части уравнений совместно, получим:
правую и левую части уравнений совместно, получим:  ,
,  .
.
Константы C 3и C 4 интегрирования найдем по начальным условиям, зная, что в момент начала движения: 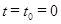 с,
с,  м,
м,  м,
м,
 м/с,
м/с,
 м/с, (НУ BDC)
м/с, (НУ BDC)
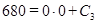 ,
,  .
.
Откуда  ,
,  .Физический смысл констант интегрирования:
.Физический смысл констант интегрирования:  м/с,
м/с,  м/с – проекции начальной скорости на оси Bx и By.
м/с – проекции начальной скорости на оси Bx и By.
Тогда:
 м/с2 – const, (19)
м/с2 – const, (19)
 (20)
(20)
Запишем, зная, что по определению  ,
,  , уравнения (19) и (20) в дифференциальной форме:
, уравнения (19) и (20) в дифференциальной форме:
 ,
,
 .
.
Разделяя переменные интегрирования, получим:
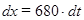 ,
,  .
.
Интегрируя  ,
,  правую и левую части уравнений совместно, получим:
правую и левую части уравнений совместно, получим:  ,
,  .
.
Константы 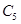 и
и  интегрирования найдем по начальным условиям (НУ BDC).
интегрирования найдем по начальным условиям (НУ BDC).
 ,
, 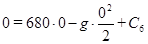 . Откуда
. Откуда  ,
, 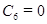 . Физический смысл констант интегрирования:
. Физический смысл констант интегрирования:  м,
м,  м – начальные координаты материальной точки. Тогда
м – начальные координаты материальной точки. Тогда
 , (21)
, (21)
 . (22)
. (22)
Совокупность уравнений (18)–(22) – уравнения движения свободной материальной точки на участке BDC.
Положив  ? с,
? с,  ? м/с,
? м/с, 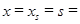 ? м,
? м, 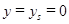 м в уравнениях (20)–(22), получим:
м в уравнениях (20)–(22), получим:
 , (20*)
, (20*)
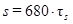 , (21*)
, (21*)
 (22*)
(22*)
и определим s, t s, vC.
Из уравнения (22*) найдем:
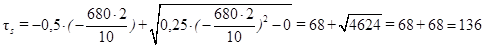 с.
с.
Решая уравнения (6*) и (7*), получим:
 м/с,
м/с,
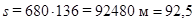 км.
км.
Скорость  падения материальной точки на землю равна:
падения материальной точки на землю равна:
 м/с.
м/с.
Положив в уравнении (20)  м, получим
м, получим  и найдем время
и найдем время  подъема на наибольшую высоту
подъема на наибольшую высоту  :
:  с.
с.
Положив в уравнении (22) 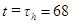 с,
с,  ?, найдем наибольшую высоту
?, найдем наибольшую высоту  подъема:
подъема:  23120 м=23,12 км.
23120 м=23,12 км.
Задание Д.6. Применение основных теорем динамики к исследованию движения материальной точки
Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости (таблица 10). Найти скорость шарика в положениях В и С и силу давления шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28 и 29 шарик, пройдя путь h 0, отделяется от пружины. Необходимые для решения данные приведены в таблице 11.
В задании приняты следующие обозначения: m – масса шарика; uА – начальная скорость шарика; t – время движения шарика на участке АВ (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27 и 30) или на участке BD (в вариантах 3, 4, 6, 7, 9–13, 15–17, 19, 22, 25, 26, 28 и 29); f – коэффициент трения скольжения шарика по стенке трубки; h 0 – начальная деформация пружины; h – наибольшее сжатие пружины; с – коэффициент жесткости пружины; H – наибольшая высота подъема шарика; s – путь, пройденный шариком до остановки.
Таблица 10 – Схемы механизмов к заданию Д.6

Продолжение таблицы 10

Продолжение таблицы 10

Таблица 11 – Исходные данные к заданию Д.6
| Номер варианта | m, кг | vA, м/с | t, с | R, м | f | a, град | β, град | h 0, см | с, Н/см | Величины, которые требуется определить дополнительно | |
| 0,5 | 2,0 | 2,0 | 0,20 | – | – | – | |||||
| 0,6 | 0.2 | 4,0 | 0,10 | – | – | H | |||||
| 0,4 | 2,0 | 0,2 | 0,15 | – | vD | ||||||
| 0,2 | 0,5 | 1,0 | 0,10 | – | – | – | vD | ||||
| 0,1 | 1,5 | 2,0 | 0,20 | – | – | – | – | ||||
| 0,3 | 2,0 | 4,0 | 0,10 | vD | |||||||
| 0,4 | 1,0 | 1,0 | 0,10 | – | vD | ||||||
| 0.2 | 0,5 | 1,5 | 0,15 | h | |||||||
| 0,5 | 1,5 | 4,0 | 0,25 | – | – | vD | |||||
| 0,4 | 0,1 | 0,5 | 0,10 | 0,2 | 0,2 | vD | |||||
| 0.2 | 1,0 | 1,0 | 0,30 | – | – | vD, h | |||||
| 0.4 | 0,4 | 2,0 | 0,20 | – | – | vD | |||||
| 0.3 | 0,1 | 1,0 | 0,10 | vD | |||||||
| 0,6 | 2,0 | 3,0 | 0,20 | – | – | s | |||||
| 0,1 | 0,1 | 1,0 | 0,15 | 0,2 | vD | ||||||
| 0,4 | 0,2 | 2,0 | 0,40 | – | – | vD | |||||
| 0,2 | од | 1,0 | 0,20 | – | 1,0 | vD | |||||
| 0,3 | 0,4 | 1,5 | 0,10 | – | – | – | – | ||||
| 0,1 | 0,1 | 0,4 | 0,30 | 0,5 | vD | ||||||
| 0.2 | 1,0 | 0,5 | 0,10 | – | 1,2 | h | |||||
| 0.7 | 0,3 | 0,3 | 0,20 | – | – | – | |||||
| 0,4 | 0,2 | 0,2 | 0,40 | – | 1,1 | vD, h | |||||
| 0,6 | 0,4 | 0,2 | 0,20 | – | – | – | |||||
| 0,5 | 0.5 | 0,6 | 0,30 | – | – | H | |||||
| 0,1 | 0,2 | 0,5 | 0,25 | – | 0,4 | vD | |||||
| 0,2 | 0,1 | 0,2 | 0,20 | – | – | – | vD | ||||
| 0,8 | 0,2 | 0,4 | 0,15 | – | – | – | vD | ||||
| 0,3 | 0,1 | 0,6 | 0,35 | 0,1 | vD | ||||||
| 0,5 | 0,2 | 0,5 | 0,20 | 0,8 | vD | ||||||
| 0,8 | 0,3 | 0,6 | 0J5 | – | tDE | ||||||






