Даны схема механизма в заданном положении (рисунок 3 а) и следующие исходные данные: ОА = АВ = 30 см; АС = 15 см; w OA = 4 рад/с; e OA = 8 рад/с2.
Решение.
1. Определение скоростей точек и угловой скорости звена (рисунок 3 б). Вычислим модуль скорости точки А кривошипа ОА в заданном положении. Так как кривошип испытывает вращательное движение вокруг неподвижной точки О, то
 см/с.
см/с.

Рисунок 3 – Схема механизма (а) и схема для определения скоростей (б)
Вследствие вращения кривошипа вектор скорости точки А перпендикулярен кривошипу и направлен в соответствии с w OA. Вектор скорости точки В ползуна направлен вдоль прямой ОВ. Зная скорость точки А и направление скорости точки В (принадлежащих звену АВ), можно определить мгновенный центр скоростей РАВ шатуна АВ. Он находится в точке пересечения перпендикуляров, восстановленных из точек А и В по отношению к направлениям их скоростей.
Модули скоростей точек В и С определятся соответственно:
 ;
; 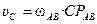 . (1)
. (1)
Угловую скорость звена АВ можно определить как
 . (2)
. (2)
Подставив выражение для w AВ в уравнения (1), получим:
 ;
; 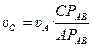 . (3)
. (3)
Расстояния APAB, BPAB и CPAB определяются из рассмотрения треугольников АBPAB и АCPAB:
 см;
см; 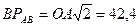 см;
см;  см.
см.
С учетом этого
 рад/с;
рад/с;  см/с;
см/с;  см/с.
см/с.
Вектор скорости точки С направлен перпендикулярно отрезку CPAB в направлении вращения звена АВ.
Скорости точек В и С можно установить и с использованием теоремы об алгебраическом равенстве проекций скоростей точек на ось, проведенную через эти точки.
В качестве прямой возьмем направление шатуна АВ. Тогда
 .
.
Из рисунка 3 б видно:  , откуда через известную
, откуда через известную  А определяем неизвестные
А определяем неизвестные  В и
В и  С:
С:  см/си
см/си 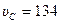 см/с.
см/с.
2. Определение ускорений точек и углового ускорения звена (рисунок 4). Ускорение  точки А складывается из вращательного
точки А складывается из вращательного  и центростремительного
и центростремительного  ускорений:
ускорений:
 ;
; 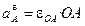 ;
; 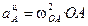 .
.
Согласно теореме об ускорениях точек плоской фигуры для ускорения точки В
имеем
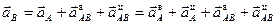 , (4)
, (4)
где 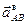 и
и  – вращательная и центростремительная составляющие ускорения точки В во вращательном движении шатуна АВ вокруг полюса А;
– вращательная и центростремительная составляющие ускорения точки В во вращательном движении шатуна АВ вокруг полюса А; 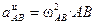 .
.

Рисунок 4 – Схемы для определения ускорений
С учетом имеющихся данных определяем модули составляющих ускорений:
 см/с2;
см/с2;  см/с2;
см/с2;  см/с2.
см/с2.
Вектор  направлен к центру вращения: от А к О. Вектор
направлен к центру вращения: от А к О. Вектор  перпендикулярен
перпендикулярен  и направлен с учетом направления
и направлен с учетом направления 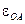 . Составляющая
. Составляющая  направлена от В к полюсу А.
направлена от В к полюсу А.
Для ускорения  точки В и его вращательной составляющей
точки В и его вращательной составляющей 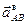 известны только линии действия этих векторов:
известны только линии действия этих векторов:  направлен вдоль линии движения ползуна ОВ;
направлен вдоль линии движения ползуна ОВ; 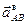 – перпендикулярно АВ.
– перпендикулярно АВ.
Зададимся произвольно их направлениями (пунктирные стрелки на рисунке 4). Определим эти ускорения из уравнений проекций векторного равенства (4) на координатные оси. Знак в ответе должен показать соответствие истинного направления вектора направлению, принятому в расчете.
Выберем направление осей х и у, как показано на рисунке 4, и составим уравнения проекций:
 , (5)
, (5)
 . (6)
. (6)
Из уравнения (6) найдем  см/с2. Истинное направление ускорения
см/с2. Истинное направление ускорения  совпадает с ускорением, построенным на рисунке 4.
совпадает с ускорением, построенным на рисунке 4.
Из уравнения (5) получим  см/с2, то есть действительное направление
см/с2, то есть действительное направление 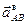 противоположно показанному на рисунке 4.
противоположно показанному на рисунке 4.
Теперь определяем угловое ускорение звена АВ:  рад/с2.
рад/с2.
Направление углового ускорения e АВ определяется направлением вращательного ускорения 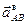 .
.
Далее определяем ускорение точки С. Согласно теореме об ускорениях точек плоской фигуры:
 ;
;  ;
;  .
.
Модули вращательного и центростремительного ускорения точки С во вращательном движении АВ вокруг полюса А соответственно:
 см/с2;
см/с2;  см/с2.
см/с2.
Направления  и
и  показаны на рисунке 2.
показаны на рисунке 2.
Ускорение точки С находим способом проекций (см. рисунок 4):
 см/с2;
см/с2;  см/с2;
см/с2;
 см/с2.
см/с2.
Векторы ускорений  и
и  точек В и С соответственно показаны на рисунке 4.
точек В и С соответственно показаны на рисунке 4.
Задание К.7. Определение абсолютной скорости и абсолютного ускорения точки
Материальная точка М движется относительно движущегося тела D. Определить для момента времени t = t 1 абсолютные скорость и ускорение точки М по заданным уравнениям относительного движения точки М и уравнениям движения тела D. Исходные данные, необходимые для расчета, приведены в таблице 7, а схемы механизмов приведены в таблице 8.
Примечания
1. Для каждого варианта положение точки М на схеме соответствует положительному значению sr.
2. В вариантах 5, 10, 12, 13, 20–24, 28–30 ОМ = sr – дуга окружности.
3. На схемах 5, 10, 12, 21, 24 ОМ – дуга, соответствующая меньшему центральному углу.
4. Относительное движение точки М в вариантах 6 и 27 и движение тела D в вариантах 23 и 29 определяются уравнениями, приведенными в последнем столбце.
Таблица 7 – Исходные данные к заданию К.7
| Вариант | Уравнение относительного движения точки М OM = sr = sr (t), см | Уравнение движения тела | t 1, с | R, см | а, см | a, град | Дополнитель-ные данные | |
| φ e = φ e (t), рад | xe = xe (t), см | |||||||
| 18sin(p t /4) | 2 t 3 – t 2 | – | 2/3 | – | – | |||
| 20sin(p t) | 0,4 t 2 + t | – | 5/3 | – | – | |||
| 6 t 3 | 2 t + 0,5 t 2 | – | – | – | ||||
| 10sin(p t /6) | 0,6 t 2 | – | – | – | ||||
| 40pcos(p t /6) | 3 t – 0,5 t 3 | – | – | – | ||||
| – | – | 3 t + 0,27 t 3 | 10/3 | – | – | φ r = 0,15p t 3 | ||
| 20cos(2p t) | 0,5 t 2 | – | 3/8 | – | ||||
| 6(t + 0,5 t 2) | t 3 – 5 t | – | – | – | ||||
| 10(1 + sin(2p t)) | 4 t + 1,6 t 2 | – | 1/8 | – | – | – | ||
| 20pcos(p t /4) | 1,2 t – t 2 | – | 4/3 | – | ||||
| 25sin(p t /3) | 2 t 2 – 0,5 t | – | – | – | ||||
| 15p t 3/8 | 5 t – 4 t 2 | – | – | |||||
| 120p t 2 | 8 t 2 – 3 t | – | 1/3 | – | – | |||
| 3 + 14sin(p t) | 4 t – 2 t 2 | – | 2/3 | – | – | |||
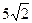 (t 2 + t) (t 2 + t)
| 0,2 t 3 + t | – | – | |||||
| 20sin(p t) | t – 0,5 t 2 | – | 1/3 | – | – | |||
| 8t 3 – 2 t | 0,5 t 2 | – | – | 
| – | |||
| 10 t + t 3 | 8 t – t 2 | – | – | – | ||||
| 6 t + 4 t 3 | t + 3 t 2 | – | – | – | ||||
| 30pcos(p t /6) | 6 t + t 2 | – | – | – | ||||
| 25p(t + t 2) | 2 t – 4 t 2 | – | 1/2 | – | – | |||
| 10psin(p t /4) | 4 t – 0,2 t 2 | – | 2/3 | – | – | |||
| 6p t 2 | – | – | – | – | φ = p t 3/6; O 1 O = O 2 A = 20 см | |||
| 75p(0,1 t + 0,3 t 3) | 2 t – 0,3 t 2 | – | – | – | ||||
| 15sin(p t /3) | 10 t – 0,1 t 2 | – | – | – | – | |||
| 8cos(p t /2) | –2p t 2 | – | 3/2 | – | – | |||
| – | – | 50 t 2 | – | – | φ r = 5p t 3/48 | |||
| 2,5p t 2 | 2 t 3 – 5 t | – | – | – | ||||
| 5p t 3/4 | – | – | – | – | φ = p t 3/8; O 1 O = O 2 A = = 40 см | |||
| 4p t 2 | – | t 3 + 4 t | – | – |
Таблица 8 – Схемы механизмов к заданию К.7

Продолжение таблицы 8

Продолжение таблицы 8







