Одной из основных задач эконометрического анализа является прогнозирование значений зависимой переменной при определенных значениях Хпр объясненной переменной.
Предположим, что мы построили некое эмпирическое значение парной регрессии ỹi=b0+b1xi, на основе кот-го хотим предсказать среднюю величину зависимой переменной у при х=хпр. В данном случае рассчитанное по уравнению величина ỹпр=b0+b1xпр является только оценкой для искомого матожидания.
Встает вопрос насколько эта оценка отклоняется от среднего матожидания для того, чтобы ей можно было доверять с надежностью γ=1-α.
Чтобы построить доверит интервал, покажем, что случайная величина ỹпр имеет норм распределение с некоторыми конкретными переменными.
Мы знаем, что ỹпр=b0+b1xпр. Подставим в это уравнение значение для bo и b1, найденное в виде лин комбинаций выборочных величин объясняющей переменной yi.
Т.е. расчетная величина действительного имеет норм распред-ие и мы находим матожидание и дисперсию.
М(Ỹпр)=M(bo+b1Xпр)= βo+Xпрβ1
D(Ỹпр)=D(bo+b1Xпр) = D(bo)+X²прM(b1)=2cov(bo,b1Xпр)***=
Рас-м вел-ну ковариации.
Заменим вел-ну bo ч/з правило ее вычисления из эмпир ур-ия регр-ии, аналог-но поступим со знач-ем βо, записав его знач-ие ч/з теорет ур-ие регр-ии.
Тогда получаем
-
это дисп-ия для значения b1 
Мы знаем вел-ну дисп bo и b1. Подставим сюда их значения:
Преобразуем данное выр-ие прибавив и отняв к скобке 
В этом выр-ии заменяем σ² несмещенной оценкой по эмпир ур-ию регр-ии σ²=∑ei²/n-2 и тогда мы м рассчитать Т стат-ку
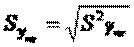, получаемого из значения теорет дисп-ии заменой дисп теорет откл-ия σ² на So², вычис-ое по выборке ∑ei²/n-2. Используя табл. Стьюдента, можем вычесть вероятность того, что |T|≤tрасч
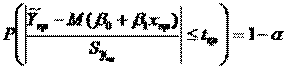
Тогда 
ν=n-2.
Таким образом, сделав такие же преобразования как для коэффициентов в уравнения, получаем, что
Классическая парная регрессионная модель. Спецификация модели.
Спецификация парной линейной регр. модели имеет вид: Y=a+bX+ε, где a и b – параметры модели (постоянные неизвестные коэфф-ты), Х – экзогенная переменная (регрессор), У – эндогенная переменная (отклик), ε – случайное возмущение, характеризующее отклонение f(x)= a+bX (теоретической линей зависимости) и возникающее:
- из-за ошибок спецификации
- из-за ошибок измерений
Уравнения для отдельных наблюдений зависимой переменной У записываются в виде (схема Гаусса-Маркова)
Yt=a+bXt+εt, t=1,…,n – выборочные данные, n – объём выборки.
Относительно возмущений εt, в регр.моделях принимаются след. предположения (условия Гаусса-Маркова)
