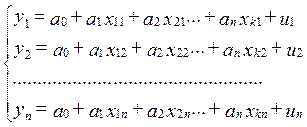Модель множественной регрессии имеет вид:
Алгоритм использования процедуры «ЛИНЕЙН» в приложении EXCEL:
1.Подготовка таблицы исходных данных (Записываем в столбцы значения переменных).
| A | B | |||
| y1 | x11 | … | xk1 | |
| y2 | x12 | … | xk2 | |
| … | … | … | … | … |
| n | yn | x1n | … | xkn |
| n+1 | ||||
| n+2 | ||||
| n+3 | ||||
| n+4 | ||||
| n+5 |
2.Вызов процедуры «ЛИНЕЙН» (Выделяем диапазон ячеек 5×(k+1), нажимаем на значок функции, в диалоговом окне «Категория» выбираем, «Статистические» в диалоговом окне «Выберите функцию» - «Линейн»; щелкнуть мышью по кнопке ОК).
3.Ввод исходных данных в процедуру (В строчке «Известные_значения_y» диалогового окна указать адрес диапазона значений эндогенной переменной yt, а в строчке «Известные_значения_х» - адрес диапазона известных значений предопределенных переменных x11:xkn; в строчку «Конст» диалогового окна занести цифру 1, если есть свободный член и 0, если его нет. В строчку «Статистика» диалогового окна занести цифру 1, Нажать клавиши Ctrl + Shift + Enter).
4. Анализ результата
| A | B | |||
| y1 | x11 | … | xk1 | |
| y2 | x12 | … | xk2 | |
| … | … | … | … | … |
| n | yn | x1n | … | xkn |
| n+1 |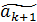 
| 
| … | 
|
| n+2 | 
| 
| … | 
|
| n+3 |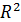 
| 
| #Н/Д | #Н/Д |
| n+4 | Fтест |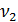 
| #Н/Д | #Н/Д |
| n+5 | 
| 
| #Н/Д | #Н/Д |
Оценивание регрессионной модели с фиктивной переменной наклона
Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. В регрессионных моделях применяются фиктивные переменные двух типов: переменные сдвига и переменные наклона.
Фиктивная переменная наклона изменяет наклон линии регрессии. При помощи фиктивных переменных наклона можно построить кусочно-линейные модели, которые позволяют учесть структурные изменения в экономических процессах (например, введение новых правовых или налоговых ограничений, изменение политической ситуации и т. д.). Для учета возможного изменения наклона графика модели при изменении градации качественного фактора предлагается ввести в спецификацию модели еще одно слагаемое вида «d умноженное на x».
Спецификация регрессионной модели в этом случае (например, для парной регрессионной модели, для простоты) имеет вид:
dt = 0 – до структурных изменений
1 – после структурных изменений,
dt - бинарная переменная
Фиктивная переменная входит в уравнение в мультипликативной форме. Оценки параметров рассчитываются с помощью метода наименьших квадратов. Параметр при фиктивной переменной характеризует степень изменения наклона графика функции регрессии под воздействием качественного фактора.
