Содержание
1. Автокорреляция случайного возмущения. Причины. Последствия.
2. Алгоритм проверки адекватности парной регрессионной модели.
3. Алгоритм проверки значимости регрессора в парной регрессионной модели.
4. Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.
5. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений.
6. Гетероскедастичность случайного возмущения. Причины.
7. Динамическая модель из одновременных линейных уравнений (привести пример).
8. Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие.
9. Индивидуальная оценка значения зависимой переменной
10. Интервальная оценка индивидуального значения зависимой переменной
11. Классическая парная регрессионная модель. Спецификация модели. Теорема Гаусса - Маркова.
12. Коэффициент детерминации в регрессионной модели.
13. Ковариация, коэффициент корреляции и индекс детерминации.
14. Количественные характеристики взаимосвязи пары случайных переменных.
15. Коэффициент корреляции и индекс детерминации.
16. Линейная модель множественной регрессии.
17. Метод наименьших квадратов: алгоритм метода; условия применения
18. Метод показателей информационной ёмкости
19. Методы подбора переменных в модели множественной регрессии.
20. Методы сглаживания временного ряда.
21., 52. Модели временных рядов.
22. Модели с бинарными фиктивными переменными.
23. Модели с частичной корректировкой
24. Настройка модели с системой одновременных уравнений
25., 26. Нелинейная модель множественной регрессии (Кобба-Дугласа. Оценка её коэффициентов.
27. Нормальный закон распределения как характеристика случайной переменной.
28. Обобщенный метод наименьших квадратов
29., 30. Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение.
31. Определение соответствия распределения случайных возмущений нормальному закону распределения
32. Основные числовые характеристики вектора остатков в классической множественной регрессионной модели
33. Отражение в модели влияния неучтённых факторов.
34. Отражение в эконометрических моделях фактора времени.
35., 36., 45. Оценивание линейной модели множественной регрессии в Excel.
37. Оценивание регрессионной модели с фиктивной переменной наклона
38. Оценка коэффициентов модели Самуэльсона-Хикса
39. Оценка параметров множественной регрессионной модели методом наименьших квадратов.
40. Оценка параметров парной регрессионной модели методом наименьших квадратов.
41. Оценка статистической значимости коэффициентов модели множественной регресии
42. Подбор переменных в модели множественной регрессии.на основе метода оценки информационной ёмкости
43. Подбор переменных в модели множественной регрессии методом «снизу вверх».
44. Подбор переменных в модели множественной регрессии методом исключения переменных («сверху вниз»)
46. Последствия гетероскедастичности. Тест GQ
47. Применение теста Стьюдента в процедуре подбора переменных в модели множественной регресии.
48. Применение фиктивных переменных при исследовании сезонных колебаний: спецификация модели, экономический смысл параметров при фиктивных переменных.
49. Принципы спецификации эконометрических моделей и их формы.
50. Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности
51. Прогнозирование экономических переменных. Проверка адекватности модели
53. Регрессионные модели с фиктивными переменными.
54. Свойства временных рядов
55. Составление спецификации модели временного ряда.
56., 57. Спецификация и оценивание МНК эконометрических моделей нелинейных по параметрам.
58. Спецификация моделей со случайными возмущениями и преобразование их к системе нормальных уравнений)
59. Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов
60. Статистические свойства оценок параметров парной регрессионной модели
61. Статистические характеристики выборки и генеральной совокупности статистических данных. Их соотношения.
62. Схема Гаусса – Маркова.
63. Теорема Гаусса - Маркова.
64. Тест ошибочной спецификации Рамсея.
65. Тест Стьюдента
66., 67. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей.
68. Устранение автокорреляции в парной регрессии.
69. F -тест качества спецификации множественной регрессионной модели.
70. Фиктивная переменная наклона: назначение; спецификация
71. Функция регрессии как оптимальный прогноз.
72. Характеристики сервиса «Описательная статистика».
73. Метод наибольшего правдоподобия
74. Что такое стационарный процесс
75. Эконометрика, её задача и метод.
76. Экспоненциальное сглаживание временного ряда.
77. Этапы построения эконометрических моделей.
78. Этапы решения экономико-математических задач.
1. Автокорреляция случайного возмущения. Причины. Последствия.
Модель называется автокоррелированной, если не выполняется третья предпосылка теоремы Гаусса-Маркова: Cov(ui,uj)≠0 при i≠j. Те между ними есть зависимость.
Есть положительная автокорреляция, где за положительным отклонением следует положительное, за отрицательным – отрицательное. Отрицательная автокорреляция - за положительным чаще всего следует отрицательное.
Автокорреляция чаще всего появляется в моделях временных рядов и моделировании циклических процессов
Причина – неправильный выбор спецификации модели.
Последствия автокорреляции
- оценки коэффициентов теряют эффективность;
- стандартные ошибки коэффициентов занижены
Типы автокорреляции
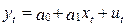
Модели с автокоррелированными остатками называются авторегрессионными. Рассматриваем модель парной регрессии,
Авторегрессия 1-го порядка: AR(1)
Авторегрессия 5-го порядка: AR(5)
Автокорреляция скользящих средних 3-го порядка:
 |
2. Алгоритм проверки адекватности парной регрессионной модели.
Адекватность – возможность получения результата с удовлетворительной точностью. Применительно к построению эконометрических моделей под точностью результата понимается абсолютное значение разности между прогнозом, полученным с помощью модели и реальным значением эндогенной переменной. Модель считается адекватной, если эта разность не превосходит некоторого наперед заданного.
1.Вся имеющаяся в распоряжении выборка наблюдений делится на две неравные части: обучающую и контролирующую. Обучающая выборка включает основную (большую) часть наблюдений. Контролирующая выборка содержит до 5% от общего объема выборки
2.По обучающей выборке оценивается модель (рассчитываются оценки параметров модели и их стандартные ошибки).
3.Задается значение доверительной вероятности Рдов =1-α и определяется критическое значение дроби Стьюдента tкрит
4.Для каждой «точки» из контролирующей выборки по известным значениям экзогенных переменных строится доверительный интервал прогнозного значения эндогенной переменной.
5.Проверяется, попадает ли соответствующее значение эндогенной переменной внутрь полученного.
Пункты 5 и 6 проводятся для каждой точки выборки персонально!
Вывод. Если все значения эндогенных переменных из контрольной выборки накрываются соответствующими доверительными интервалами, то полученная модель с вероятностью Рдов считается адекватной, т.е. пригодной для дальнейшего использования в целях решения экономических задач
3. Алгоритм проверки значимости регрессора в парной регрессионной модели
При проверке качества спецификации парной регрессии наиболее важной является задача установления наличия линейной зависимости между эндогенной переменной и регрессором модели. С этой целью проверяют значимость оценки параметра b.
Алгоритм проверки значимости параметра b выполняется в следующей последовательности:
1) оценка параметров парной регрессии
2) оценка дисперсии возмущений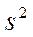 
3) оценка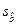 
среднего квадратичного отклонения параметра b
4) выбор значения tкр (по заданному уровню значимости альфа и числу степеней свободы (n-2) из таблиц распределения Стьюдента)
5) проверка неравенства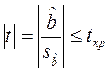 
при Н0: b=0
Если данное неравенство выполняется, то регрессор признается незначимым, если не выполняется, то данная гипотеза отвергается и регрессор признается значимым, т.е. между эндогенной переменной и регрессором присутствует линейная зависимость.
