9.1. Значення рядів динаміки та їх види
9.2. Основні характеристики рядів динаміки
9.3. Вирівнювання динамічних рядів
9.4. Виявлення та вимірювання сезонних коливань
9.5. Аналіз рядів динаміки і прогнозування
Термінологічний словник
| № з/п | Термін | Визначення |
| Ряд динаміки | Перелік числових значень певного статистичного показника у послідовні моменти або періоди часу | |
| Абсолютний приріст | Показник, який показує, на скільки одиниць в абсолютному виражені рівень одного періоду більше або менше певного попереднього рівня | |
| Темп зростання | Відносний показник, який показує, в скільки разів рівень даного періоду більше або менше базового рівня | |
| Темп приросту | Відносний показник, який показує, на скільки відсотків один рівень більше (або менше) базового рівня | |
| Абсолютне значення 1 % приросту | Показник, який показує, скільки становить один відсоток приросту показника у грошовому вираженні |
Питання для самоконтролю
9.1. Дайте визначення динамічного ряду. Наведіть основні елементи.
9.2. Наведіть основні види рядів динаміки.
9.3. Поясніть суть базисних і ланцюгових характеристик динаміки. Що вони показують?
9.4. Наведіть основні причини виникнення не співставлення динамічних рядів.
9.5. Які особливості обчислення середнього рівня інтервального динамічного ряду?
9.6. Які особливості обчислення середнього рівня моментного динамічного ряду?
9.7. Що характеризує показник абсолютного приросту і як він розраховується?
9.8. За якою формулою розраховують середній темп зростання?
9.9. Як розрахувати середній темп приросту?
9.10. Як обчислити середні показники ряду динаміки?
9.11. Що Ви розумієте під загальною тенденцією розвитку?
9.12. Які існують прийоми вирівнювання рядів динаміки?
9.13. Який порядок виявлення сезонних коливань?
Розв’язок типових завдань
Завдання 9.1
Необхідно:
За даними таблиці 9.8 визначити: 1) базові і ланцюгові характеристики динаміки: абсолютні прирости, темпи зростання і приросту, абсолютні значення 1 % приросту; 2) середньорічні темпи зростання і абсолютні прирости за 1985 – 1990 та 1991 – 1995 рр.
Дані для виконання:
Таблиця 9.8. Динаміка виробництва промислових роботів в об’єднанні
| Рік | 1985 | 1990 | 1995 |
| Кількість, шт. |
Розв’язок. Абсолютний приріст Dt показує, на скільки одиниць власного виміру рівень ряду yt більший (+) чи менший (–) за рівень, взятий за базу порівняння (yt- 1 чи y 0):
ланцюговий Dt= yt – yt- 1,
базовий D t = yt – y 0.
Так, за 1985 – 1990 рр. виробництво промислових роботів зросло на 54 шт. (114 – 60), за 1990 – 1995 рр. – на 12 шт. (126 – 114). За весь період абсолютний приріст становив 66 шт. (126 – 60).
Темп зростання показує, в скільки разів один рівень ряду більший за інший:
ланцюговий tt = 
;
базовий 
.
За 1985 – 1990 рр. виробництво роботів збільшилось в 1,9 рази (114: 60), за 1990 – 1995 рр. – в 1,1 рази (126: 114). Базовий темп зростання за весь період становив 2,1 рази (126: 60).
Темп приросту показує, на скільки процентів значення yt більше (+) чи менше (–) за рівень, який прийнятий за 100%: 
.
У нашому прикладі темпи приросту становлять:
− ланцюгові 190 – 100 = 90%, 110 – 100 = 10%;
− базовий – 210 – 100 = 110%.
Абсолютне значення 1% приросту можна обчислити як частку відділення абсолютного приросту на темп приросту: 
; 54: 90 = 0,60; 66: 110 = 0,60, тобто вага відносно приросту є не що інше, як сота частина рівня, взятого за базу порівняння.
Середньорічний абсолютний приріст – це середнє з ланцюгових абсолютних приростів: 
, де уп – кінцевий рівень ряду.
За 1985 – 1990 роки 
= 54: 5 = 10,8; за 1990 – 1995 роки = 12: 5 = 2,4.
Середньорічний темп зростання визначають за формулою середньої геометричної
.
У нашому прикладі за 1985 – 1990 рр.
;
за 1990 – 1995 рр.
.
Середньорічний приріст виробництва промислових роботів за 1985 – 1990 роки становив 17,4%, за 1990 – 1995 роки – 2,5%.
Прискорення (сповільнення) зростання обчислюють зіставленням однойменних характеристик швидкості зростання. Наприклад, абсолютних приростів: 
.
Значення d t < 0 свідчить про сповільнення зростання. Темп сповільнення абсолютної швидкості обчислюють відношенням абсолютних приростів
Прискорення (сповільнення) відносної швидкості є частка від ділення середньорічних темпів зростання. Дільником виступає більший за значенням. У нашому прикладі 
.
Завдання для самопідготовки
Завдання 9.2
Необхідно:
– дати повну і змістовну відповідь на наступні питання.
Дані для виконання:
1. Види й основні характеристики рядів динаміки.
2. Вирівнювання динамічних рядів.
3. Виявлення та вимірювання сезонних коливань.
4. Аналіз рядів динаміки і прогнозування рівнів ряду.
Завдання 9.3
Необхідно:
– за даними таблиці 9.9 обчислити базисні і ланцюгові характеристики динаміки: абсолютні прирости, темпи зростання і темпи приросту.
Дані для виконання:
Таблиця 9.9. Динаміка витрат на збут ВАТ “Дніпро”
| Роки | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
| Витрати на збут, млн. грн. | 2000,0 | 2344,0 | 1997,0 | 2450,0 | 3430,0 | 3540,0 | 5567,0 |
Завдання 9.4
Необхідно:
– за даними таблиці 9.10 обчислити базисні характеристики динаміки: абсолютні прирости і темпи приросту.
Дані для виконання:
Таблиця 9.10. Динаміка собівартості ВАТ “Нортон”
| Роки | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
| Собівартість товарів, млн. грн. | 17855,0 | 66778,0 | 55734,0 | 66790,0 | 266750,0 | 99543,0 | 46678,0 |
Завдання 9.5
Необхідно:
– за даними таблиці 9.11 обчислити ланцюгові характеристики динаміки: абсолютні прирости і темпи приросту, абсолютні значення 1% приросту. Показати взаємозв’язок названих характеристик.
Дані для виконання:
Таблиця 9.11. Динаміка виробництва будівельної цегли в регіоні, млн. шт.
| Рік | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
| Кількість, млн. шт. |
Завдання 9.6
Необхідно:
– за даними таблиці 9.12, використовуючи взаємозв’язок характеристик динаміки, визначити обсяги виробництва пральних машин, абсолютну та відносну швидкість його зростання.
Дані для виконання:
Таблиця 9.12. Ланцюгові характеристики динаміки виробництва пральних машин
| Рік | Виробництво пральних машин, тис. шт. | Ланцюгові характеристики динаміки | |||
| абсолютний приріст, тис. шт. | темп зростання, % | темп приросту, % | абсолютне значення 1% приросту, тис. шт. | ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| – | – | – | – | ||
| ? | ? | ? | ? | ? | |
| ? | ? | ? | 3,9 | ||
| ? | ? | ? | 6,6 | ? | |
| ? | ? | 102,1 | ? | ? | |
| ? | ? | ? | ? |
Завдання 9.7
Необхідно:
– за даними таблиці 9.13 визначити вид ряду динаміки, середньорічні темпи росту (зменшення), побудуйте прогноз на 2008 рік та відобразіть його графіком.
Дані для виконання:
Таблиця 9.13. Випуск продукції промисловості області характеризується такими даними за 2001-2008 рр.
| Роки | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
| Випуск продукції промисловості, млн. грн. | 3440,0 | 4435,0 | 5554,0 | 3456,0 | 5561,0 | 3345,0 | 8133,0 |
Завдання 9.8
Необхідно:
– за даними таблиці 9.14 визначити прогностичні рівні обсягу виробництва на 2005 рік та середньорічні темпи їх зниження (зростання).
Дані для виконання:
Таблиця 9.14. Виробництво основних видів продовольчих товарів на душу населення області характеризується такими даними за 2003 – 2007 рр.
| Продукти, кг | Роки | ||||
| 2003 | 2004 | 2005 | 2006 | 2007 | |
| М’ясо | 53,2 | 47,8 | 39,3 | 28,4 | 24,3 |
| Молоко | 123,9 | 108,8 | 78,8 | 53,7 | 50,1 |
| Цукор-пісок | 130,9 | 92,0 | 69,9 | 76,5 | 70,2 |
| Олія | 20,6 | 19,3 | 16,4 | 15,4 | 15,2 |
| Хлібопродукти | 129,0 | 128,6 | 123,5 | 104,3 | 111,2 |
Завдання 9.9
Необхідно:
– за даними таблиці 9.15 розрахувати абсолютний приріст, темп зростання, темп приросту базисним і ланцюговим способами, середньорічний темп зростання власного капіталу.
Дані для виконання:
Таблиця 9.15. Динаміка власного капіталу підприємств Житомирської області
| Роки | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
| Власний капітал, млн. грн. | 2000,0 | 2344,0 | 1997,0 | 2450,0 | 3430,0 | 3540,0 | 5567,0 |
Тестові завдання
для підсумкового контролю знань
9.1 Рядом динаміки називається:
а) ряд даних, розміщених у певній послідовності;
б) ряд, що відображає інтенсивність поширення явища за певний період;
в) це послідовність чисел, які характеризують зміну того чи іншого явища за певний період часу;
г) це перелік явищ та числових даних, що їм відповідають.
9.2 Рівнем ряду називають:
а) числові дані того чи іншого показника ряду динаміки;
б) перелік хронологічних дат або інтервалів часу;
в) явища, які потребують дослідження;
г) відповіді а і б.
9.3 Часом ряду є:
а) числові дані того чи іншого показника ряду динаміки;
б) перелік хронологічних дат або інтервалів часу;
в) явища, що потребують дослідження протягом деякого проміжку часу;
г) відповіді б і в.
9.4 Залежно від реєстрації фактів ряди бувають:
а) моментні і неперервні;
б) моментні і інтервальні;
в) дискретні і неперервні;
г) дискретні і ряди середніх.
9.5 Інтервальним рядом називають:
а) ряд, рівні якого характеризують явище за певний період часу;
б) такі ряди динаміки, які характеризують узагальнюючі показники розвитку явища;
в) такі ряди динаміки, рівні яких фіксують стан явища на даний момент часу;
г) такі ряди динаміки, які порівнюють розвиток певного явища зі станом цього явища на певний момент часу.
9.6 До дискретних рядів належать:
а) моментні ряди;
б) інтервальні ряди;
в) ряди середніх;
г) варіанти а, б, в.
9.7 Моментними рядами динаміки називають:
а) такі ряди динаміки, які характеризують узагальнюючі показники розвитку явища;
б) такі ряди динаміки, які визначають розвиток явища протягом тривалого, раніше встановленого для дослідження проміжку часу;
в) такі ряди динаміки, рівні яких фіксують стан явища на даний момент часу;
г) такі ряди динаміки, які порівнюють розвиток певного явища зі станом цього явища на певний момент часу.
9.8 Інтервальним рядом динаміки є:
а) вартість основних виробничих засобів підприємства станом на 01.01. року;
б) випуск продукції підприємства по місяцям;
в) відповіді а і б;
г) правильної відповіді немає.
9.9 Зрівняність ряду динаміки шляхом, при якому враховується сутність та мета явища, досягається однорідність економічного змісту показників ряду, називається:
а) однаковий підхід до одиниць сукупності;
б) забезпечення однакової повноти охоплення різних частин явища;
в) єдиної методології розрахунку рівнів динамічного ряду;
г) приведення рядів динаміки до однієї основи.
9.10 Суттю показника ряду динаміки, який називається абсолютним приростом, є:
а) показує, на скільки взятий рівень відрізняється від рівня, взятого за базу порівняння;
б) характеризує швидкість змін рівнів ряду і розраховується як відношення взятого рівня до попереднього;
в) відповідає швидкості зміни рівнів ряду і розраховується як різниця рівнів ряду;
г) характеризує вагомість кожного відсотка приросту.
Проблемні напрями досліджень
для підготовки доповідей та реферативних робіт
1. Застосування методів рядів динаміки в практичній діяльності підприємства
2. Прогнозування діяльності підприємств України
ТЕМА 10. IНДЕКСНИЙ МЕТОД
10.1. Сутність, призначення та види індексів
10.2. Загальні агрегатні та середньозважені індекси кількісних та якісних показників
10.3. Індекси середнього рівня
10.4. Ланцюгові та базисні індекси
10.5. Взаємозв’язок між індексами та визначення ролі окремих факторів в динаміці складних показників
Термінологічний словник
| № з/п | Термін | Визначення |
| 1 | 2 | 3 |
| Індекси | Відносні величини, що характеризують співвідношення явищ у часі, просторі і порівняно з планом | |
| Індексний метод | Обчислення зведених індексів, що виступають як узагальнюючі відносні показники, що дозволяють зіставляти між собою показники за складними сукупностями | |
| Індивідуальні індекси | Відносні показники, що характеризують зміну у динаміці величини окремого елемента складного явища | |
| Зведені (загальні) індекси | Відносні показники динаміки та порівняння таких складних сукупностей, окремі елементи яких не можна підсумовувати | |
| Агрегатний індекс | Загальний індекс, одержаний шляхом зіставлення підсумків, що виражають величину складного показника у звітному і базовому періодах за допомогою сумірників (незмінних) | |
| Базисні індекси | Індекси, що передбачають порівняння показників з одним, взятим за базу | |
| Ланцюгові індекси | Індекси, що передбачають порівняння кожного наступного періоду з попереднім | |
| Динамічні індекси | Індекси, що характеризують зміну явища за певний проміжок часу | |
| Територіальні індекси | Індекси, що представляють собою зіставлення показників за географічними територіями (країнами, регіонами, областями) | |
| Індекси порівняння з планом | Індекси, що характеризують зміни господарської діяльності суб’єктів господарювання в поточному періоді порівняно з встановленим планом (стандартом, нормою) | |
| Індекси кількісних показників | Індекси, що характеризують зміну обсягу того чи іншого явища | |
| Індекси якісних показників | Індекси, що характеризують зміну якісної ознаки, що відображає особливості розвитку явища |
Питання для самоконтролю
10.1. Що Ви розумієте під індексом?
10.2. Які функції виконують індекси?
10.3. Які розрізняють види індексів залежно від ступеня охоплення одиниць сукупності, бази порівняння, об’єкта порівняння та характеру досліджуваних об’єктів?
10.4. Які особливості розрахунку індивідуальних та зведених індексів?
10.5. Що Ви розумієте під агрегатними індексами?
10.6. Як розрахувати агрегатний індекс вартості продукції (товарообороту)?
10.7. Який існує взаємозв’язок між індексами фізичного обсягу, цін та товарообороту?
10.8. Які особливості розрахунку індексів змінного, фіксованого складу та структурних зрушень?
10.9. Чи існує взаємозв’язок між ланцюговими та базисними індексами?
10.10. Який існує взаємозв’язок між індексами фізичного обсягу, цін та товарообороту?
10.11. Яким чином за допомогою зведених індексів можна визначити
в абсолютному вираженні зміну товарообороту за рахунок зміни обсягу
продажу та цін?
Розв’язок типових завдань
Завдання 10.1
Необхідно:
– за даними табл. 10.4 визначити індивідуальні індекси цін, фізичного обсягу реалізованого товару та товарообороту; загальні індекси: товарообороту, цін, фізичного обсягу реалізації;
– показати взаємозв’язок загальних індексів;
– обчислити абсолютний приріст товарообороту в цілому та за рахунок кожного фактора.
Дані для виконання:
Таблиця 10.4. Дані про зміни в реалізації верхнього одягу в ТзОВ “Одяг”
| Пальта | Ціна за одиницю товару, грн. | Кількість реалізованого товару, шт. | ||
| базовий період, р0 | поточний період, р1 | базовий період, q0 | поточний період, q1 | |
| Чоловічі | ||||
| Жіночі |
Розв’язок. Індивідуальні індекси обчислюють окремо для кожної групи товарів. Індивідуальний індекс цін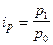 
, для чоловічих пальт 
, або 101,2 %, а для жіночих – 
, або 140,3 %. Значення обох індексів свідчать про підвищення цін як на чоловічі (+1,2 %), так і на жіночі (+40,3 %) пальта.
Аналогічно визначають індивідуальні індекси фізичного обсягу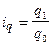 
, для чоловічих пальт 
, або 121,2 %, для жіночих – 
, або 68,8 %. Отже, кількість проданих чоловічих пальт зросла на 21,2 % в поточному періоді порівняно з базовим, а кількість реалізованих жіночих пальт зменшилась на 31,2 %.
Загальний індекс товарообороту в цілому по магазину обчислюють за формулою:
, або 112,9 %, тобто у поточному місяці порівняно з базовим загальний товарооборот збільшився на 12,9 %.
Це збільшення може відбуватися під впливом двох факторів – цін та обсягу реалізації товарів. Визначимо вплив кожного фактора окремо за відповідними формулами.
Загальний індекс цін 
, або 111,0 %. Це означає, що за рахунок підвищення цін товарооборот збільшився на 11 %.
Загальний індекс фізичного обсягу реалізації обчислюють за формулою 
, або 101,7 %. Отже, за рахунок зміни кількості реалізованого товару товарооборот в цілому збільшився на 1,7 %.
Система співзалежних індексів матиме вигляд
або 112,9 %.
Абсолютний приріст обчислюють як різницю між чисельником і знаменником відповідних індексів.
Абсолютний приріст товарообороту в цілому становить, грн.:
грн.,
за рахунок факторів:
грн.
грн.
Виручка від реалізації збільшилася в цілому на 8756 грн., а завдяки підвищенню цін – на 7626 грн., а за рахунок збільшення кількості проданого товару виручка збільшилась на 1130 грн.
Завдання 10.2
Необхідно:
– за даними таблиці 10.5 обчислити індекси середніх витрат матеріалу змінного, фіксованого складу і структурних зрушень;
– перевірити взаємозв’язок між трьома індексами.
Дані для виконання:
Таблиця 10.5. Дані про витрати матеріалу на 1 виріб за період та кількість виготовлених виробів
| Технологія розкрою матеріалу | Витрати матеріалу на 1 виріб за місяць, м | Кількість виготовлених виробів за місяць, тис. шт. | ||
| базовий, x0 | поточний, x1 | базовий, f0 | поточний, f1 | |
| Традиційна | 0,9 | 0,7 | ||
| Удосконалена | 0,6 | 0,4 | ||
| Разом | – | – |
Розв’язок. Індекс змінного складу середніх витрат матеріалу обчислюють за формулою:
,
або 61,5 %. Отже, середні витрати матеріалу в поточному періоді порівняно з базовим скоротилися на 38,5 %.
Індекс фіксованого складу визначають наступним чином:
або 71,8 %. Це означає, що за рахунок економії матеріалу в розрахунку на один виріб по кожній технології середні витрати матеріалу зменшились на 28,2 %.
Індекс структурних зрушень розраховують за формулою:
, або 85,6 %.
За рахунок структурних зрушень, тобто збільшення частки вдосконаленої технології в загальному обсязі виробництва, середні витрати матеріалу на один виріб зменшились на 14,4 %.
Взаємозв’язок між індексами перевіряють наступним чином:
.
Завдання 10.3
Необхідно:
– визначити загальний індекс цін за даними таблиці 10.6.
Дані для виконання:
Таблиця 10.6. Дані про товарообіг звітного періоду та розмір зниження цін
| Товари | Товарооборот звітного періоду, млн грн. | Розмір зниження цін, % | Індивідуальні індекси цін |
| р1q1 | ір | ||
| Радіоприймачі | -15 | 0,85 | |
| Телевізори | -27 | 0,73 | |
| Разом | х | х |
Розв’язок. Обчислимо загальний індекс цін, використовуючи формулу середньо гармонійного індексу цін:
або 77 %
Висновок: товарооборот радіоприймачів та телевізорів за рахунок зниження цін зменшився на 23 %.
Завдання для самопідготовки
Завдання 10.4
Необхідно:
– за даними таблиці 10.7 обчислити загальний індекс фізичного обсягу, товарообороту і цін, індивідуальні індекси ціни і обсягу.
Дані для виконання:
Таблиця 10.7. Дані про реалізацію продуктів і їх цінах на колгоспному ринку
| Продукти | Одиниця виміру | Базисний період | Звітний період | ||
| обсяг продажу | ціна, грн. | обсяг продажу | ціна, грн. | ||
| Цукор | кг | 2,5 | 3,5 | ||
| Олія | л | 3,8 | 4,0 |
Завдання 10.5
Необхідно:
– за даними таблиці 10.8 розрахувати загальні індекси: 1) цін; 2) товарообороту; 3) кількості проданого товару.
Дані для виконання:
Таблиця 10.8. Дані про реалізацію продукції
| Продукція | Товарооборот за місяць, тис. грн. | Індивідуальні індекси цін | |
| базовий | поточний | ||
| Зернові культури | 86,7 | 113,4 | 2,41 |
| Соняшник | 95,6 | 107,2 | 2,75 |
Завдання 10.6
Необхідно:
– за даними таблиці 10.9 обчислити загальні індекси витрат на виробництво двох видів продукції і за рахунок змін у кількості продукції;
– розрахувати розмір економії (перевитрат) від змін у собівартості одиниці продукції.
Дані для виконання:
Таблиця 10.9. Загальні витрати на виробництво двох видів продукції
| Назва продукції | Загальні витрати на виробництво продукції за період, тис. грн. | Темпи приросту (зменшення) кількості продукції, % | |
| Базисний | Поточний | ||
| Годинники | 12,5 | 14,8 | +15 |
| Телерадіотовари | 8,3 | 9,5 | -8 |
Завдання 10.7
Необхідно:
– за даними таблиці 10.10 визначити індивідуальні індекси кількості проданої продукції; загальні індекси кількості проданої продукції, цін та товарообороту; збільшення (зменшення) товарообороту за рахунок змін кількості проданої продукції та цін.
Дані для виконання:
Таблиця 10.10. Дані про товарооборот та зміну кількості проданих товарів
| Продукція | Товарооборот в фактичних цінах, грн. | Збільшення (+), зменшення (–) кількості проданих продуктів, % | |
| Базисний період | Звітний період | ||
| Картопля | +11,7 | ||
| Морква | -18,8 | ||
| Цибуля | +13,1 |
Завдання 10.8
Необхідно:
– за даними таблиці 10.11 обчислити: індивідуальні індекси цін та обсягу реалізації; загальні індекси цін, фізичного обсягу та товарообороту.
Дані для виконання:
Таблиця 10.11. Дані про реалізацію продуктів на ринку міста
| Продукти | Обсяг реалізації, кг | Ціна за одиницю, грн. | ||
| Базисний період | Звітний період | Базисний період | Звітний період | |
| Плоди та ягоди | 2,5 | 3,1 | ||
| Виноград | 6,3 | 7,8 | ||
| Овочі | 0,8 | 0,7 |
Завдання 10.9
Необхідно:
– за даними таблиці 10.12 обчислити: індивідуальні індекси цін та обсягу реалізації; загальні індекси цін, фізичного обсягу, товарообороту; абсолютну зміну товарообороту за рахунок змін обсягу продажу та цін на продукти в звітному періоді порівняно з базисним.
Дані для виконання:
Таблиця 10.12. Дані про реалізацію продуктів ТзОВ “Крамниця”
| Продукти | Обсяг продажу, тис. одиниць | Ціна за одиницю, грн. | ||
| Базисний період | Звітний період | Базисний період | Звітний період | |
| Свинина, кг | 33,0 | 38,5 | ||
| Яловичина, кг | 30,0 | 35,0 | ||
| Молоко, л | 4,0 | 4,3 |
Завдання 10.10
Необхідно:
– за даними таблиці 10.13 обчислити загальні індекси витрат на виробництво; собівартості одиниці продукції; фізичного обсягу продукції.
Дані для виконання:
Таблиця 10.13. Дані ВАТ “Укр-зв’язок” щодо випуску телефонів
| Вид продукції | 2005 р. | 2006 р. | ||
| вироблено, шт. | собівартість одиниці, тис. грн. | вироблено, шт. | собівартість одиниці, тис. грн. | |
| Телефони “Samsung” | 1,0 | 1,33 | ||
| Телефони “Siemens” | 0,6 | 1,00 |
Завдання 10.11
Необхідно:
– за даними таблиці 10.14 обчислити загальні індекси витрат на виробництво; собівартості одиниці продукції; фізичного обсягу продукції.
Дані для виконання:
Таблиця 10.14. Дані заводу ЗАТ “Верстат-маш” щодо випуску верстатів-автоматів
| Вид продукції | 2005 р. | 2006 р. | ||
| вироблено, шт. | собівартість одиниці, тис. грн. | вироблено, шт. | собівартість одиниці, тис. грн. | |
| Верстати-автомати | 1,5 | 1,8 | ||
| Верстати-напівавтомати | 1,7 | 1,9 |
Завдання 10.12
Необхідно:
– за даними таблиці 10.15 розрахувати індекси змінного, фіксованого складу та структурних зрушень.
Дані для виконання:
Таблиця 10.15. Дані про кількість вкладів та середній розмір вкладу серед міського та сільського населення
| Вид населення | Кількість вкладів на кінець року, тис. шт. | Середній розмір вкладу, грн. | ||
| базовий | поточний | базовий | поточний | |
| Міське | ||||
| Сільське | ||||
| Разом | х | х |
Завдання 10.13
Необхідно:
– за даними таблиці 10.16 обчислити індекси змінного, фіксованого складу та структурних зрушень.
Дані для виконання:
Таблиця 10.16. Дані про середньорічну чисельність працівників та їх середньомісячну заробітну плату
| Вид транспорту | Середньорічна чисельність працівників, тис. чол. | Середня місячна зарплата працівників, грн. | ||
| Базисний рік | Звітний рік | Базисний рік | Звітний рік | |
| Залізничний | ||||
| Водний | ||||
| Разом | – | – |
Завдання 10.14
Необхідно:
– за даними таблиці 10.17, використовуючи взаємозв’язок індексів, дати відповіді на питання по кожному місяцю.
Дані для виконання:
Таблиця 10.17. Динаміка показників оплати праці ТзОВ “Професія”
| Показник | Зміни у порівнянні з попереднім місяцем: + збільшення, – зменшення | ||
| Січень | Лютий | Березень | |
| Фонд заробітної плати | ? | -23 | +45 |
| Середня заробітна плата | +23 | -17 | ? |
| Кількість робітників | -15 | ? | +38 |
Тестові завдання
для підсумкового контролю знань
10.1. Індекс – це:
а) узагальнюючий відносний показник, який виражає співвідношення величин складного економічного явища, що складається з адитивних елементів;
б) абсолютний показник, який виражає зміну економічного явища у часі та просторі;
в) узагальнюючий відносний показник, який виражає співвідношення величин складного економічного явища, що складається з елементів безпосередньо неадитивних;
г) абсолютний показник, який виражає зміну елементів складного економічного явища у часі та просторі.
10.2. За ступенем охоплення одиниць сукупності індекси поділяються на:
а) базисні та ланцюгові;
б) індивідуальні та загальні;
в) агрегатні та середні з індивідуальних індексів;
г) індекси об’ємних та якісних показників.
10.3. За характером досліджуваних об’єктів індекси поділяються на:
а) індивідуальні та зведені;
б) агрегатні та середні з індивідуальних індексів;
в) базисні та ланцюгові;
г) індекси об’ємних та якісних показників.
10.4. Залежно від бази порівняння індекси поділяються на:
а) індекси об’ємних та якісних показників;
б) базисні та ланцюгові;
в) агрегатні та середні з індивідуальних індексів;
г) індивідуальні та загальні.
10.5. Індекси, що характеризують зміну у динаміці величини окремого елемента складного явища, називаються:
а) індивідуальними;
б) субіндексами;
в) базисними;
г) ланцюговими.
10.6. Індекси, що характеризують зіставлення показників за географічними територіями, називаються:
а) загальними;
б) субіндексами;
в) територіальними;
г) ланцюговими.
10.7. Між базисними та ланцюговими індексами існує наступний зв’язок:
а) прямий;
б) зворотний;
в) добуток базисних індексів дорівнює ланцюговому останнього періоду;
г) добуток ланцюгових індексів дорівнює базисному останнього періоду.
10.8. При розрахунку індексів використовуються наступні види статистичних середніх:
а) арифметична і геометрична;
б) арифметична і гармонійна;
в) квадратична і гармонійна;
г) геометрична і квадратична.
10.9. Існує взаємозв’язок між загальними індексами фізичного обсягу, цін та товарообороту:
а) загальний індекс товарообороту дорівнює добутку загального індексу фізичного обсягу та загального індексу цін;
б) загальний індекс фізичного обсягу дорівнює добутку загального індексу товарообороту та загального індексу цін;
в) загальний індекс цін дорівнює добутку загального індексу товарообороту та загального індексу фізичного обсягу;
г) загальний індекс товарообороту дорівнює сумі загального індексу фізичного обсягу та загального індексу цін.
10.10. Існує взаємозв’язок між індексами середнього рівня:
а) індекс фіксованого складу дорівнює добутку індексу змінного складу та індексу структурних зрушень;
б) індекс змінного складу дорівнює добутку індексу фіксованого складу та індексу структурних зрушень;
в) індекс структурних зрушень дорівнює добутку індексу фіксованого складу та індексу змінного складу;
г) індекс фіксованого складу дорівнює різниці індексу змінного складу та індексу структурних зрушень.
Проблемні напрями досліджень
для підготовки доповідей та реферативних робіт
1. Способи розрахунку абсолютних та відносних показників динаміки та індексів: порівняльний аспект.
2. Класифікація індексів в різних літературних джерелах.
