6.1. Середні показники: суть, завдання, наукові основи обчислення
6.2. Види середніх показників та способи їх розрахунку
6.3. Мода і медіана: поняття та порядок обчислення
6.4. Варіація ознак та варіаційні ряди
6.5. Узагальнюючі показники варіації
Термінологічний словник
| № з/п | Термін | Визначення |
| 1 | 2 | 3 |
| Середній показник | Узагальнююча або типова характеристика суспільних явищ за однією кількісною ознакою | |
| Мода | Значення ознаки, яке найчастіше зустрічається у ряді розподілу | |
| Медіана | Числове значення ознаки одиниці сукупності, яке розташоване посередині ранжированого ряду і ділить його на дві рівні частини | |
| Варіація ознак | Наявність відмінностей у числових значеннях ознак одиниць статистичної сукупності | |
| Варіаційний ряд | Групова таблиця з двома графами – групування одиниць за однією кількісною ознакою і чисельність одиниць у кожній групі | |
| Дискретний ряд | Ряд розподілу, який утворюється за дискретною ознакою, кількість значень якої обмежена і приймає цілі числові значення | |
| Інтервальний ряд | Ряд розподілу, який об’єднує варіанти безперервних ознак або ознак, що змінюються у широких межах дискретних ознак | |
| Розмах варіації | Абсолютна величина різниці між максимальним і мінімальним значеннями (варіантами) ознаки. Розмах варіації є показником загальної оцінки варіації і визначає межі, в яких коливаються значення ознак статистичної сукупності. | |
| Середнє лінійне відхилення | Середня арифметична з абсолютних відхилень конкретних варіант від їх середнього значення. | |
| Дисперсія | Середня з квадратів відхилень конкретних варіант від їх середнього значення. | |
| Середнє квадратичне відхилення | Квадратний корінь з дисперсії | |
| Осереднювана ознака | Ознаку, за якою знаходиться середня |
Питання для самоконтролю
6.1. Що розуміють під середніми величинами?
6.2. Для чого використовують середні величини?
6.3. Які існують вимоги до обчислення середніх?
6.4. Які види середніх величин Ви знаєте? Які особливості їх розрахунку?
6.5. Чим відрізняються прості і зважені середні показники?
6.6. Які особливості розрахунку середніх гармонійної і квадратичної?
6.7. Що означає поняття варіації ознак?
6.8. Що розуміють під варіацією і частотою варіаційного ряду?
6.9. Які види варіаційних рядів Ви знаєте?
6.10. Які ознаки показників варіації існують? Як вони розраховуються?
6.11. Що розуміють під модою? Які особливості її розрахунку?
6.12. Що розуміють під медіаною? Як вона розраховується?
Розв’язок типових завдань
Завдання 6.1
Необхідно:
– за даними таблиці 6.10 визначити середній час очікування тролейбусів за даними результатів разового вибіркового опитування робітників і службовців одного з обласних центрів.
Дані для виконання:
Таблиця 6.10. Дані вибіркового опитування робітників і службовців щодо часу очікування тролейбусів
| Середній час очікування, хв. | До 4 | 5–9 | 10–14 | 15–19 | 20 і більше | Разом |
| Чисельність опитаних, % до підсумку |
Розв’язок. При визначенні середньої з інтервального ряду насамперед слід обчислити середину інтервалу кожної з груп як напівсуму нижньої і верхньої меж інтервалу. Якщо ряд розподілу має відкриті інтервали, то їх розмір приймається умовно рівним інтервалу тієї групи, що розташована поруч.
Так, для першої групи це буде інтервал наступної, тобто другої групи, а для останньої – інтервал передостанньої групи. Слід зауважити, що за даними ряду розподілу середня обчислюється як арифметична зважена. Роль ваги при визначені середньої в наведеному прикладі відіграють частки опитаних:
= 
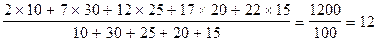хв.
Отже, середній час очікування тролейбусів становить 12 хв.
Завдання 6.2
Необхідно:
– використовуючи дані таблиці 6.11, що характеризують чисельність студентів, прийнятих до навчальних закладів країни, і тих, які були прийняті на денне відділення, визначити середню частку студентів, прийнятих на денне відділення в базовому і поточному навчальних роках.
Дані для виконання:
Таблиця 6.11. Дані про кількість студентів, прийнятих на денне відділення в базовому і поточному роках
| Навчальні заклади | Базовий рік | Поточний рік | ||
| всього прийнято студентів, тис. чол. | частка прийнятих на денне відділення, % | прийнято студентів на денне відділення, тис. чол. | частка прийнятих на денне відділення, % | |
| Вищі | 181,7 | 58,8 | 113,4 | 65,3 |
| Системи підготовки молодших фахівців | 264,6 | 62,8 | 157,4 | 66,3 |
Розв’язок. При визначенні середньої частки слід насамперед усвідомити економічний зміст осереднюваного показника, тобто:
= 
Знаменник цього співвідношення відіграє роль ваги при визначенні середньої, щодо базового навчального року. Цей показник відомий, чисельник же наведеного вище співвідношення легко обчислити, помноживши частку студентів, прийнятих на денне відділення, на загальну чисельність прийнятих студентів. Отже, в цьому випадку слід використати формулу середньої арифметичної зваженої:
= 
, або 61,2 %.
Середня частка студентів, прийнятих на денне відділення в базовому навчальному році, становить 61,2%.
Даних про загальну чисельність прийнятих студентів у поточному році немає, але цей показник можна визначити, поділивши чисельність студентів, зарахованих на денне відділення, на їх частку у загальній кількості прийнятих. Виходячи з цього, для обчислення середньої частки студентів денного відділення треба використати формулу середньої гармонійної зваженої, тобто
= 
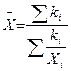, або 65,9 %.
Завдання 6.3
– за даними таблиці 6.12 визначити модальний та медіанний вік чоловіків-одинаків за даними перепису населення України.
Дані для виконання:
Таблиця 6.12. Дані про групування чоловіків-одинаків за віком
| Вік х, років | до 20 | 20–29 | 30–39 | 40–49 | 50–59 | 60–69 | 70 і старше | Разом |
| Частка вікової групи w, % | 4,9 | 20,1 | 15,5 | 15,2 | 17,0 | 13,0 | 14,3 | 100,0 |
Розв’язок. Модальний вік розраховують за формулою
,
де XMo – нижня межа; hMo – ширина модального інтервалу;
fMo, fMo-1, fMo+1 – відповідна частота (частка) модального, попереднього і наступного інтервалів відносно модального. Модальний віковий інтервал становить від 20 до 29 років, оскільки йому відповідає найбільша частота
(fMo = 20,1):
років,
тобто найбільш поширеним віком серед чоловіків-одинаків є вік близько 27 років.
Медіанний вік визначають за формулою:
,
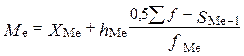де X Me, h Me – відповідно нижня межа і ширина медіанного інтервалу;
S Me-1 – сума накопичених частот (часток) в інтервалі, що передує медіанному;
f Me – частота медіанного інтервалу.
Порядковий номер центральної варіанти відповідає частці 50. У графі накопичених частот ця варіанта знаходиться в групі 40 – 49 років. Отже:
років.
Половина чоловіків-одинаків має вік до 45,6 років.
Завдання 6.4
– визначити розмах варіації і коефіцієнт осциляції; середнє лінійне відхилення і лінійний коефіцієнт варіації.
Дані для виконання:
Вік робітників однієї бригади будівельників становить 28, 30, 31, 46, 47, 48, 50 років.
Розв’язок. Розмах варіації – це різниця між максимальним і мінімальним значенням ознаки, тобто
R = x max – x min = 50 – 28 = 22 років.
Відношення розмаху варіації до середньої величини ознаки називають коефіцієнтом осциляції, який обчислюють за формулою
.
Оскільки дані не згруповані, середню величину обчислюють за формулою середньої арифметичної простої
років,
тоді
Середнє лінійне відхилення – це середній модуль відхилень індивідуальних значень ознаки від їх середньої величини
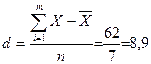років.
Лінійний коефіцієнт варіації визначають за формулою:
,
що свідчить про незначну варіацію робітників бригади будівельників щодо їх віку.
Завдання 6.5
Необхідно:
– за даними розподілу вантажних автомобілів одного підприємства за строком експлуатації (таблиця 6.13) обчислити: дисперсію строку експлуатації вантажних автомобілів; середнє квадратичне відхилення і квадратичний коефіцієнт варіації; дисперсію частки вантажних автомобілів зі строком експлуатації менше 8-ми років.
Дані для виконання:
Таблиця 6.13. Розрахункова таблиця для обчислення показників варіації
| Строк перебування вантажних автомобілів в експлуатації, років | Кількість автомо-білів | Середина інтервалу, хі | 
| 
| 
| 
| 
| 
|
| До 4 | -7 | |||||||
| 4 – 6 | -4 | |||||||
| 6 – 8 | -2 | |||||||
| 8 – 10 | ||||||||
| 10 –12 | ||||||||
| 12 –14 | ||||||||
| 14 і більше | ||||||||
| Разом | - | - | - | - |
Розв’язок. Дисперсія – це середній квадрат відхилень від середньої:
s 
.
В рядах розподілу середню обчислюють за формулою середньої арифметичної зваженої
років;
s 
.
Дисперсію можна визначити також за формулою різниці квадратів
s 
,
де 
– середній квадрат значень варіант.
Необхідні для обчислення дані наведені в таблиці.
Отже,
s 
Середнє квадратичне відхилення – це корінь квадратний з дисперсії
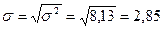років.
Відношення середнього квадратичного відхилення до середньої називають квадратичним коефіцієнтом варіації. Його обчислюють за формулою:
,
що свідчить про однорідність сукупності автомобілів щодо строку 
перебування їх в експлуатації і типовість середньої для цієї сукупності.
Частка автомобілів, у яких строк перебування в експлуатації менше 8-ми років становить
Дисперсію частки як альтернативної ознаки визначають за формулою:
s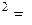 
p (1 – p), тобто s 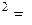0,43 (1 – 0,43) = 0,245.
Завдання для самопідготовки
Завдання 6.6
Необхідно:
– визначити середню тривалість переговорів опитаних абонентів.
Дані для виконання:
В результаті вибіркового опитування десяти абонентів зареєстровано таку тривалість міжміських телефонних переговорів із зарубіжжям, хв.: 7; 10; 5; 10; 7; 6; 10; 8; 12; 5.
Завдання 6.7
Необхідно:
– за даними таблиці 6.14 визначити середній виробіток і середню заробітну плату одного робітника.
Дані для виконання:
За перший квартал є наступні дані по підприємству (таблиця 6.14).
Таблиця 6.14. Дані про кількість робітників та фонд оплати праці
ВАТ “Метан”
| Форма оплати праці | Кількість робітників, чол. | Середній виробіток, грн. | Фонд заробітної плати, тис. грн. |
| Погодинна | 570,5 | 1712,0 | |
| Відрядна | 668,6 | 2021,2 |
Завдання 6.8
Необхідно:
– за даними таблиці 6.15 розрахувати середню кількість працівників в установах зв’язку м. Кривий Ріг.
Дані для виконання:
Таблиця 6.15. Дані про чисельність працівників і кількість відділень установ зв’язку м. Кривий Ріг
| Чисельність працівників, чол. | 3 | 4 | 5 | 6 | Разом |
| Кількість відділень, од. |
Завдання 6.9
Необхідно:
– за даними таблиці 6.16 обчислити середній, модальний та медіанний розміри житлової площі за результатами вибіркового обстеження.
Дані для виконання:
Таблиця 6.16. Групування сімей за житловою площею, що припадає на одного члена сім’ї
| Група сімей за житлоплощею на одного члена сім’ї, кв. м | до 5 | 5–7 | 7–9 | 9–11 | 11–13 | 13–15 | Разом |
| Кількість сімей, од. |
Завдання 6.10
Необхідно:
– за даними таблиці 6.17 визначити середню, моду і медіану на основі наведених нижче даних про розподіл ткаль за їх денним виробітком.
Дані для виконання:
Таблиця 6.17. Дані про групування ткаль за денним виробітком тканини
| Група ткаль за денним виробітком, м | до 60 | 60 – 70 | 70 – 80 | 80 – 90 | 90 і більше | Разом |
| Чисельність ткаль, чол. |
Завдання 6.11
Необхідно:
– за даними таблиці 6.18 розрахувати середній процент браку.
Дані для виконання:
Таблиця 6.18. Виявлена бракована продукція за окремими групами консервів
| Групи консервів | Забраковано товарів | |
| Разом, тис. умовних банок | Частка від загального обсягу перевірених банок, % | |
| М’ясні | 50,5 | 4,2 |
| Рибні | 140,1 | 7,0 |
| Плодоовочеві | 384,4 | 10,1 |
| Разом | 575,0 | Х |
Завдання 6.12
Необхідно:
– за даними таблиці 6.19 визначити середню, модальну і медіанну величини продуктивності праці.
Дані для виконання:
Таблиця 6.19. Дані, що характеризують продуктивність праці робітників ВАТ “Світязь”
| Вироблено продукції 1 робітником за зміну, кг | 190 | 203 | 240 | 250 | 252 | 259 | 260 |
| Кількість робітників, чол. |
Завдання 6.13
Необхідно:
– за даними таблиці 6.20 визначити середній, модальний і медіанний рівні спецпідготовки персоналу.
Дані для виконання:
Таблиця 6.20. Дані про групування робітників за рівнем спецпідготовки
| Групи робітників за рівнем спецпідготовки, % | До 30,0 | 30,0–40,0 | 40,0–50,0 | 50,0–60,0 | 60,0–70,0 | Більше 70,0 |
| Кількість робітників зі спецпідготовкою, чол. |
Завдання 6.14
Необхідно:
– за даними таблиці 6.21 визначити середню, модальну та медіанну продуктивність праці.
Дані для виконання:
Таблиця 6.21. Дані про продуктивність праці працівників торговельного підприємства
| Групи працівників за розміром виробітку, грн. | До 400,0 | 400,0–600,0 | 600,0–800,0 | 800,0–1000,0 | Більше 1000,0 |
| Кількість працівників, чол. |
Завдання 6.15
Необхідно:
– за даними таблиці 6.22 обчислити середнє лінійне та середнє квадратичне відхилення, розмах варіації, лінійний та квадратичний коефіцієнти варіації, коефіцієнт осциляції.
Дані для виконання:
Таблиця 6.22. Дані про групування підприємств за рівнем товарообороту
| Група підприємств за розміром товарообороту, млн. грн. | до 4 | 4–8 | 8–12 | 12–16 | 16–20 | 20–21 | Разом |
| Кількість підприємств |
Завдання 6.16
Необхідно:
– визначити: 1) середню кількість відпрацьованих людино-днів; 2) розмах варіації; 3) середнє лінійне відхилення; 4) дисперсію; 5) середнє квадратичне відхилення; 6) лінійний і квадратичний коефіцієнти варіації; 7) коефіцієнт осциляції.
Дані для виконання:
Трудова участь членів колективу за місяць характеризується такими даними, людино-днів: 24; 25; 23; 20; 18.
Завдання 6.17
Необхідно:
– за даними таблиці 6.23 обчислити середнє лінійне та середнє квадратичне відхилення, розмах варіації. Провести їх оцінку.
Дані для виконання:
Таблиця 6.23. Групування робітників за денним виробітком тканини
| Група робітників за денним виробітком тканини, пог. м. | 20-26 | 26-32 | 32-38 | 38–44 | 44–50 | 50–56 | Разом |
| Кількість робітників |
Завдання 6.18
Необхідно:
– за даними таблиці 6.24 використовуючи ряд розподілу автомобілів автопідприємства за величиною добового пробігу, визначити: 1) середній добовий пробіг автомобіля; 2) середнє лінійне відхилення; 3) лінійний коефіцієнт варіації;
– пояснити зміст обчислених характеристик варіації.
Дані для виконання:
Таблиця 6.24. Дані про групування автомобілів за рівнем добового пробігу
| Добовий пробіг автомобілів, км | до 160 | 160–180 | 180–200 | 200 і більше | Разом |
| Всього автомобілів, од. |
Завдання 6.19
Необхідно:
– за даними таблиці 6.25 визначити лінійний і квадратичний коефіцієнти варіації віку металорізальних верстатів.
Дані для виконання:
Таблиця 6.25. Вікова структура 120 металорізальних верстатів промислового підприємства
| Вік металорізальних верстатів, років | До 10 | 10-15 | 15-20 | 20 і більше |
| Кількість верстатів, од. |
Тестові завдання
для підсумкового контролю знань
6.1.Середньою величиною показника сукупності називають:
а) типовий розмір ознаки сукупності;
б) характеристика ознаки, що знаходиться по центру ряду розподілу;
в) показник, що характеризує відношення окремих величин у сукупності;
г) повторюваний результат багаторазових вимірювань однієї і тієї ж ознаки.
6.2. Вимогою типовості середньої величини є:
а) середня не повинна підпадати під дію випадкових коливань;
б) сукупність об'єктів повинна бути якісно однорідною;
в) середня повинна обчислюватись за всім колом явищ;
г) обсяг сукупності повинен бути достатньо великим.
6.3. На основі степеневої функції розраховується середня:
а) арифметична;
б) гармонійна;
в) квадратична;
г) геометрична.
6.4. Ознакою, яка ділить ранжирований ряд розподілу на дві рівні частини, називають:
а) середньою;
б)дисперсією;
в) модою;
г) медіаною.
6.5. Абсолютну міру варіації ознаки в статистичній сукупності характеризує:
а) розмах варіації;
б) середнє лінійне відхилення;
в) середнє квадратичне відхилення;
г) дисперсія.
6.6. Наближену оцінку ступеня варіації в сукупності дає:
а) дисперсія;
б) лінійний коефіцієнт варіації;
в) квадратичний коефіцієнт варіації;
г) коефіцієнт осциляції.
6.7. Сукупність буде вважатися однорідною при такій величині коефіцієнта осциляції:
а) 0,6;
б) 1,0;
в) 1,5;
г) 2,0.
6.8. Варіація в сукупності вважається низькою при такому значенні лінійного коефіцієнта варіації:
а) 55 %;
б) 42 %;
в) 33%;
г) 20 %.
6.9. Середня величина буде вважатися типовою для сукупності, якщо значення квадратичного коефіцієнта варіації становить:
а) 12%;
б) 24 %;
в) 36 %;
г) 52 %.
6.10. Ознаку, яка найчастіше зустрічається у ряді розподілу, називають:
а) середньою.
б) дисперсією.
в) модою.
г) медіаною.
Проблемні напрями досліджень
для підготовки доповідей та реферативних робіт
1. Розрахунок середніх показників у сукупностях з високим ступенем варіації ознак.
2. Оцінка середніх рівнів динамічних рядів.
