В большинстве СМО поступления клиентов происходит случайным образом. Это означает, что наступление события (например, поступление клиента или завершение обслуживания) не зависит от времени, прошедшего с момента наступления события.
Время между последовательными поступлениями клиентов и время их обслуживания, будучи случайными, при моделировании СМО количественно описываются экспоненциальным распределением, плотность вероятности которого имеет вид
f (t) = λ ℮- λt, t >0,
причем математическое ожидание М (х) = 
.
Функция распределения экспоненциального закона F (x) = 1 - ℮- λt, t >0.
4. При обслуживании некоего сложного агрегата всегда имеется запасной блок для немедленной замены в случае поломки. Время выхода агрегата из строя является случайной величиной, распределенной по экспоненциальному закону, и в среднем происходит каждые 40 минут. Оператор, обслуживающий агрегат, утверждает, что агрегат «имеет привычку» выходить из строя каждый вечер около 20.30. Проанализировать утверждение оператора.
Решение. Средняя интенсивность (количество событий в единицу времени) агрегата равна λ =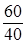 
= 1,5 отказа в час. Следовательно, плотность экспоненциального распределения времени отказа имеет вид
f (t) = 1,5℮- 1,5 t, t >0.
Что касается заявления оператора, то и без вычислений видно, что оно не может соответствовать действительности, так как не согласуется с тем, что время между отказами агрегата распределено по экспоненциальному закону и, следовательно, является случайным. Для подтверждения или опровержения заявления оператора нельзя использовать вероятность того, что отказ будет происходить в 20.30, т.к. вероятность такого события зависит от времени дня (относительно 20.30) когда она вычисляется. Например, если вычисления производятся в 20.20, то, т.к. разница с 20.30 составляет 10 минут, то вероятность того, что утверждение оператора окажется справедливым этим вечером, равна
= 0,22,
т.е. является очень малой. Если же вычисления проводить, например, в 19.00, то вероятность того, что отказ будет иметь место в 20.30, равна
= 0,91.
Таким образом, достоверность утверждения оператора нельзя проанализировать на основе полученных вероятностей. В данной ситуации нужно полагаться только на характеристики экспоненциального распределения, а точнее, на его свойство отсутствия последействия.
5. Объяснить связь между интенсивностью поступления заявок на обслуживание λ и средним временем между последовательными их поступлениями. Определите среднюю интенсивность (в час) поступлений заявок на обслуживание и среднее время между их последовательными поступлениями в следующих примерах
1) каждые 10 минут происходит одно поступление.
2) Каждые 6 минут происходит два поступления.
Решение. Средний интервал времени между поступлениями есть математическое ожидание времени между поступлениями заявок и = 1/(интенсивность поступления заявок в единицу времени).
1) λ = 
= 6 заявок в час. М (Х) = 
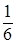часа.
2) λ = 
= 20 заявок в час. М (Х) = 
часа. ►
6. Время между последовательными поступлениями клиентов в некоторый Департамент распределено по экспоненциальному закону со средним значением 0,05 часа. Управление начинает работу в 8.00 утра.
1) Определить плотность вероятности экспоненциального распределения, описывающего время между последовательными поступлениями клиентов.
2) Определите вероятность того, что до 8.15 утра клиентов в Департаменте не будет.
3) Сейчас 8.35 утра. Последний клиент прибыл в управление в 8.26. Какова вероятность того, что следующий клиент прибудет до 8.38 утра?
4) Чему равно среднее число посетителей, которые прибудут в Департамент от 8.10 до 8.45 утра?
Решение. 1) М (Х) = 
часа. Следовательно, т.к. М (х) = , то λ = 20. Тогда плотность вероятности равна
f (t) = 20℮- 20 t, t >0.
2) Промежуток времени – 15 минут, причем нужно вычислить вероятность того, что клиентов не будет. Следовательно,
= ℮- 5 ≈ 0,00674.
3) Промежуток времени – 3 минуты, нужно вычислить вероятность того, что клиент прибудет. Поэтому
= 1 - ℮- 1 ≈ 0,6321.
4) Т.к. средняя интенсивность λ, т.е. количество клиентов за час, равна 20 посетителей, а нам нужно вычислить количество посетителей за 35 минут, имеем пропорцию
1 час – 20 посетителей,
часа – х посетителей,
откуда х = 
≈ 11,67. ►
7. Официанты О 1 и О 2 ресторана быстрого питания в ожидании посетителей заняты следующей игрой: если в течение одной минуты в ресторан не прибудет ни один посетитель, О 1 платит 2 цента О 2, в противном случае 2 цента от О 2 получает О 1. Требуется вычислить средний выигрыш официанта О 1 за восьмичасовую смену. Время между приходами посетителей распределено по экспоненциальному закону со средним значением 1,5 минуты.
Решение. Среднее значение, т.е. математическое ожидание М (Х) = 
минуты, следовательно, λ = 
посетителя в минуту. Нам нужно вычислить вероятность того, что в данную минуту не придет ни один посетитель, т.е.
≈ 0,5117.
Получили, что каждую минуту официант О 1 может заплатить 2 цента с вероятностью 0,5117 и может получить 2 цента с вероятностью 0,4883. Тогда его средний выигрыш за одну минуту будет равен
(-2)· 0,5117 + 2·0,4883 = – 0,047 цента в минуту.
За восьмичасовую смену получаем (– 0,047) · 60 · 8 = – 22,56.
Таким образом, за восьмичасовую смену официант О 1 в среднем проигрывает 22,56 цента. ►
